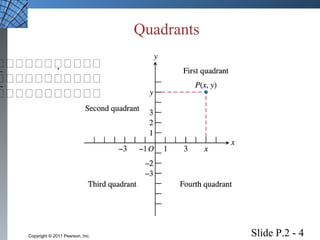
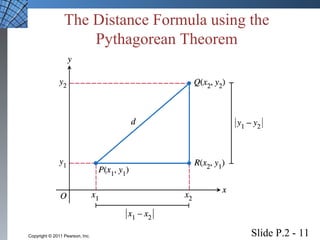
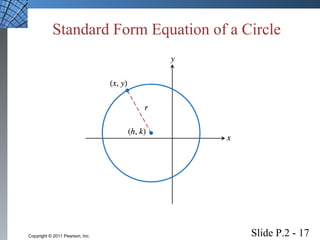
This document introduces several foundational concepts in geometry and coordinate systems, including the Cartesian coordinate plane, absolute value, distance formulas, midpoint formulas, and equations of circles. It provides definitions, examples, and step-by-step solutions for calculating distances between points, midpoints of line segments, and standard form equations of circles. The key topics covered lay the groundwork for further material in the textbook.

1. P.2
Cartesian
Coordinate
System
Copyright © 2011 Pearson, Inc.

2. What you’ll learn about
 Cartesian Plane
 Absolute Value of a Real Number
 Distance Formulas
 Midpoint Formulas
 Equations of Circles
 Applications
… and why
These topics provide the foundation for the material that
will be covered in this textbook.
Slide P.2 - 2 Copyright © 2011 Pearson, Inc.

3. The Cartesian Coordinate Plane
or Rectangular Coordinate System




Slide P.2 - 3 Copyright © 2011 Pearson, Inc.

4. Quadrants



Slide P.2 - 4 Copyright © 2011 Pearson, Inc.

5. Absolute Value of a Real Number
absolute value of a real num ber a
The is
a a
> ìï
= - < íï
î =
, if 0
a a a
| | if 0.
a
0, if 0
Slide P.2 - 5 Copyright © 2011 Pearson, Inc.

6. Example Using the Definition of
Absolute Value
Evaluate:
-7
p - 5
Slide P.2 - 6 Copyright © 2011 Pearson, Inc.

7. Solution
Evaluate:
-7 = 7
because - 7 < 0, -4 = -(-7) = 7
p - 5 = -(p - 5) = 5 -p
because p » 3.14, p - 5 < 0
Slide P.2 - 7 Copyright © 2011 Pearson, Inc.

8. Properties of Absolute Value
Let a and b be real numbers.
1. | a |³ 0
2. |-a|=|a|
3. |ab |=|a||b |
4. a
b
= |a|
|b |
, b ¹ 0
Slide P.2 - 8 Copyright © 2011 Pearson, Inc.

9. Distance Formula (Number Line)
Let a and b be real numbers.
The distance between a and b is a -b .
Note that a-b = b -a .
Slide P.2 - 9 Copyright © 2011 Pearson, Inc.

10. Distance Formula (Coordinate Plane)
y2
The distance d between points P ( x, y)
1 1 and Q ( x, 2 ) in the coordinate plane is
( )2 + y1
d = x1- x2
( )2 .
- y2
Slide P.2 - 10 Copyright © 2011 Pearson, Inc.

11. The Distance Formula using the
Pythagorean Theorem
Slide P.2 - 11 Copyright © 2011 Pearson, Inc.

12. Example Finding the Distance
Between Two Points
Slide P.2 - 12 Copyright © 2011 Pearson, Inc.

13. Solution
d = (2 - 5)2 + (7 - 3)2
= (-3)2 + (4)2
= 9 +16
= 25
= 5
Slide P.2 - 13 Copyright © 2011 Pearson, Inc.

14. Midpoint Formula (Number Line)
The midpoint of the line segment
with endpoints a and b is
a +b
2
.
Slide P.2 - 14 Copyright © 2011 Pearson, Inc.

15. Midpoint Formula (Coordinate Plane)
The midpoint of the line segment
with endpoints (a,b) and (c,d) is
a +c
2
,b +d
2
æè ç öø ÷
.
Slide P.2 - 15 Copyright © 2011 Pearson, Inc.

16. Standard Form Equation of a Circle
The standard formequation of a circle
with center (h, k)and radius r is
(x -h)2 + (y- k)2 = r2 .
Slide P.2 - 16 Copyright © 2011 Pearson, Inc.

17. Standard Form Equation of a Circle
Slide P.2 - 17 Copyright © 2011 Pearson, Inc.

18. Example Finding Standard Form
Equations of Circles
Find the standard form equation of the
circlewith center (2, - 3) and radius 4.
Slide P.2 - 18 Copyright © 2011 Pearson, Inc.

19. Example Finding Standard Form
Equations of Circles
Find the standard form equation of the
circlewith center (2, - 3) and radius 4.
(x -h)2 + (y- k)2 = r2 where h = 2, k = -3,and r = 4.
Thus the equation is (x - 2)2 + (y+ 3)2 = 16.
Slide P.2 - 19 Copyright © 2011 Pearson, Inc.

20. Quick Review
1. Find the distance between -5 and 3 .
Use a calculator to evaluate the expression. Round answers
to two decimal places.
2. 8 2 +
6
2
3. -12 +
8
2
4. 3 2 +
5
2
5. 2 − 5 + 1 −
3
( ) ( )
2 2
4 2
Slide P.2 - 20 Copyright © 2011 Pearson, Inc.

21. Quick Review Solutions
1. Find the distance between -5 and 3 .
2.75
Use a calculator to evaluate the expression. Round answers
to two decimal places.
2. 8 2 +
6
2
3. -12 +
8
2
4. 3 5
5. 2
+
− + −
2 2
10
-2
5.83
( ) ( )
2 2
4 2
5 1 3 3.61
Slide P.2 - 21 Copyright © 2011 Pearson, Inc.