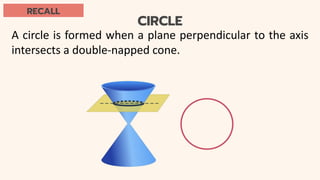
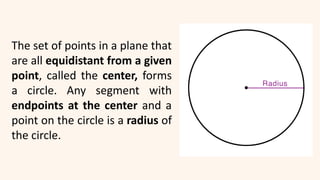
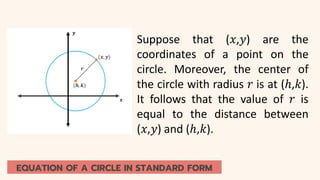
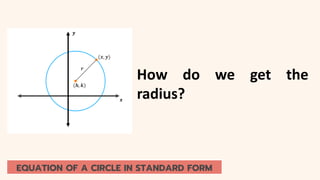
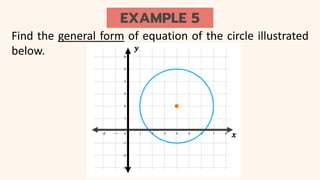
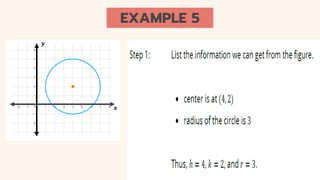
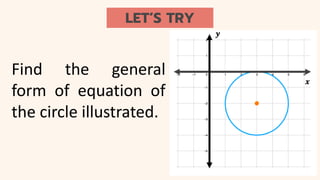
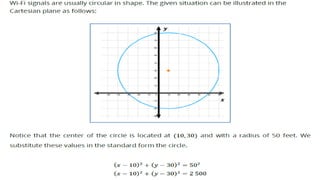
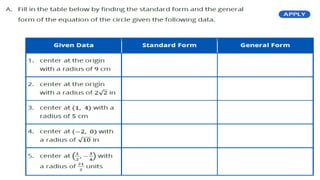
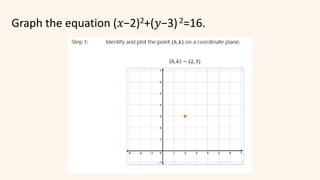
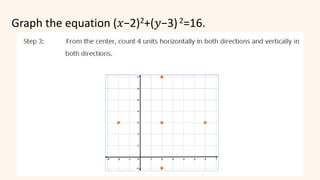
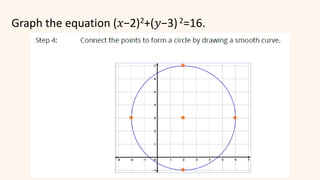
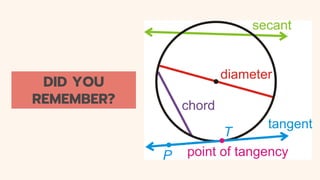
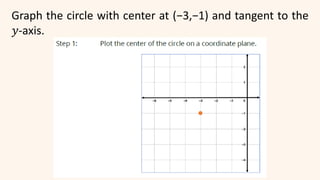
The document discusses circles and their applications. It begins by defining a circle and describing how circles are formed. It then provides examples of how circles are used in architecture, transportation, photography, and other fields. The remainder of the document discusses finding the equation of a circle, including the standard and general forms of the circle equation. It provides examples of finding the equation given the center and radius and finding the center and radius given the equation. It also demonstrates how to graph circles using software.

1. CIRCLES
02

2. CIRCLE
A circle is formed when a plane perpendicular to the axis
intersects a double-napped cone.
RECALL

3. ARCHITECTURE
Circular shapes are mostly
used as symbolic designs
in architecture around the
world. Moreover, the use
of circles is more efficient
when it comes to savings
in surface area. It also has
better behavior regarding
winds and solar radiation.
APPLICATIONS OF CIRCLES

4. TRANSPORTATION
Wheels made it easier for
people to travel great
distances. This invention has
been one of the most useful
and essential of all times. Also,
when determining distances,
GPS heavily depends on
circles. Using circle theories, it
calculates distances between
satellites and points.
APPLICATIONS OF CIRCLES

5. PHOTOGRAPHY
Adjusting camera lenses is
done by moving the lenses in a
screw-like manner. This is the
reason why camera lenses are
circular in shape. It is easier for
the photographers and
videographers to focus and
adjust the zoom lenses or the
focal lengths of their cameras.
APPLICATIONS OF CIRCLES

6. The set of points in a plane that
are all equidistant from a given
point, called the center, forms
a circle. Any segment with
endpoints at the center and a
point on the circle is a radius of
the circle.

7. Suppose that (𝑥,𝑦) are the
coordinates of a point on the
circle. Moreover, the center of
the circle with radius 𝑟 is at (ℎ,𝑘).
It follows that the value of 𝑟 is
equal to the distance between
(𝑥,𝑦) and (ℎ,𝑘).
EQUATION OF A CIRCLE IN STANDARD FORM

8. How do we get the
radius?
EQUATION OF A CIRCLE IN STANDARD FORM

9. Suppose that (𝑥,𝑦) are the
coordinates of a point on the
circle. Moreover, the center of
the circle with radius 𝑟 is at (ℎ,𝑘).
It follows that the value of 𝑟 is
equal to the distance between
(𝑥,𝑦) and (ℎ,𝑘). This may be
calculated using the distance
formula.
EQUATION OF A CIRCLE IN STANDARD FORM

10. EQUATION OF A CIRCLE IN STANDARD FORM
DISTANCE FORMULA

11. EQUATION OF A CIRCLE IN STANDARD FORM

12. EQUATION OF A CIRCLE IN STANDARD FORM
This equation is known as the standard form of
equation of a circle with center at (ℎ,𝑘) and radius 𝑟.
This is also known as the center-radius form.

13. EQUATION OF A CIRCLE IN STANDARD FORM
If a circle has the center at the origin (0,0) and has
radius 𝑟:
This is the standard form of equation of a circle with
center at the origin.

16. EXAMPLE 1
Find the equation of the circle with center at the origin
and has a radius of 10 units.

17. EXAMPLE 1
Find the equation of the circle with center at the origin
and has a radius of 10 units.

18. EXAMPLE 1
Find the equation of the circle with center at the origin
and has a radius of 10 units.

19. EXAMPLE 1
Find the equation of the circle with center at the origin
and has a radius of 10 units.

20. LET’S TRY
Find the equation of the circle with
center at the origin and has a radius of
12 units.

21. EXAMPLE 2
Find the equation of the circle with center at (−3,−1) and
has a radius of √6 units.

22. EXAMPLE 2
Find the equation of the circle with center at (−3,−1) and
has a radius of √6 units.

23. EXAMPLE 2
Find the equation of the circle with center at (−3,−1) and
has a radius of √6 units.

24. EXAMPLE 2
Find the equation of the circle with center at (−3,−1) and
has a radius of √6 units.

25. LET’S TRY
Find the equation of the circle with
center at (0,−5) and has a radius of √10
units.

26. We have learned in the first two examples how to
determine the equation of a circle given its center
and radius. What if we reverse the process?

28. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

29. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

30. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

31. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

32. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

33. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

34. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

35. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

36. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

37. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

38. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

39. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

40. EXAMPLE 3
Find the center and the radius of the circle whose
equation is (𝑥−10)2+(𝑦+8)2=49.

41. LET’S TRY
Find the center and radius of the circle
whose equation is (𝑥+1)2+(𝑦−5)2 = 20.

42. EQUATION OF A CIRCLE IN GENERAL FORM
where the numerical coefficients are real numbers and
𝐴=𝐵. Moreover, both 𝐴 and 𝐵 cannot be zero at the
same time.

43. EXAMPLE 4
Identify the center and the radius of the circle defined by
the equation 𝑥2+𝑦2+4𝑥−6𝑦+3=0.

44. EXAMPLE 4
Identify the center and the radius of the circle defined by
the equation 𝑥2+𝑦2+4𝑥−6𝑦+3=0.

45. EXAMPLE 4
Identify the center and the radius of the circle defined by
the equation 𝑥2+𝑦2+4𝑥−6𝑦+3=0.

46. EXAMPLE 4
Identify the center and the radius of the circle defined by
the equation 𝑥2+𝑦2+4𝑥−6𝑦+3=0.

47. EXAMPLE 4
Identify the center and the radius of the circle defined by
the equation 𝑥2+𝑦2+4𝑥−6𝑦+3=0.
The center is at (−𝟐,𝟑) and the radius is √𝟏𝟎.

48. LET’S TRY
Identify the center and the radius of the
circle defined by the equation
𝑥2+𝑦2 +2𝑥+2𝑦−7=0.

49. ALTERNATIVE WAY
Note: These formulas work when the value of 𝐴 and 𝐵 are both 1.

50. EXAMPLE 5
Find the general form of equation of the circle illustrated
below.

51. EXAMPLE 5

52. EXAMPLE 5

53. EXAMPLE 5

54. EXAMPLE 5
Therefore, the general form of the equation of the circle is
𝒙𝟐+𝒚𝟐−𝟖𝒙−𝟒𝒚+𝟏𝟏=𝟎.

55. LET’S TRY
Find the general
form of equation of
the circle illustrated.

56. EXAMPLE 6
Rowell’s house has a portable Wi-Fi router that can reach
a field of about 50 feet from its location. Suppose their
neighborhood represents the Cartesian plane, his location
is in the origin, and his house is situated 30 feet north and
10 feet east from where he is.
a. Find the equation of the circle in general form which
describes the boundary of the Wi-Fi signal.
b. Determine whether he can still connect to their Wi-Fi at
home.

57. EXAMPLE 6

58. EXAMPLE 6

59. EXAMPLE 6

60. LET’S TRY
A cellular network company uses towers to
transmit communication information. A
tower located at (−1,−4) of the company grid
can transmit signals up to a 7-kilometer
radius. Find the general form of equation of
the boundary this tower can transmit signals
to.

63. ASSESSMENT

66. C. Analyze and solve the problem below.
The Pampanga Eye currently holds the title for
the tallest Ferris wheel in the Philippines. It is
situated in Sky Ranch Pampanga, a theme park
in San Fernando City. The Ferris wheel is 50
meters in diameter and has a height of 65
meters. Find an equation for the wheel,
assuming that its center lies on the 𝑦-axis and
that the ground is the 𝑥-axis.
ASSESSMENT

67. FAST WAY TO GRAPH CONIC
SECTIONS USING SOFTWARE
TOOLS
https://www.symbolab.com/solver/conic-sections-
calculator

68. EXAMPLE
Graph the equation 𝑥2+𝑦2=36.

69. Graph the equation 𝑥2+𝑦2=36.

70. Graph the equation 𝑥2+𝑦2=36.

71. Graph the equation 𝑥2+𝑦2=36.

72. EXAMPLE
Graph the equation (𝑥−2)2+(𝑦−3)2=16.

73. Graph the equation (𝑥−2)2+(𝑦−3)2=16.

74. Graph the equation (𝑥−2)2+(𝑦−3)2=16.

75. Graph the equation (𝑥−2)2+(𝑦−3)2=16.

76. Graph the equation (𝑥−2)2+(𝑦−3)2=16.

77. EXAMPLE
Graph the circle with center at (−3,−1) and tangent to the
𝑦-axis.

78. DID YOU
REMEMBER?

79. Graph the circle with center at (−3,−1) and tangent to the
𝑦-axis.

80. Graph the circle with center at (−3,−1) and tangent to the
𝑦-axis.

81. Graph the circle with center at (−3,−1) and tangent to the
𝑦-axis.

82. PERFORMANCE
TASK

83. A. Graph the circle with the given center and radius.
1. (1,3); 𝑟=2
2. (−2,2); 𝑟=3
B. Graph the circle with the given equation in standard form.
3. (𝑥−2)2+(𝑦+3)2=36
C. Graph the circle with the given equation in general form.
4. 𝑥2+𝑦2+4𝑥−6𝑦+12=0
D. Sketch the graph and find the equation in standard form of
the circle being described in each item.
5. a circle with center at (3,4) and tangent to the 𝑥-axis
PERFORMANCE TASK 2