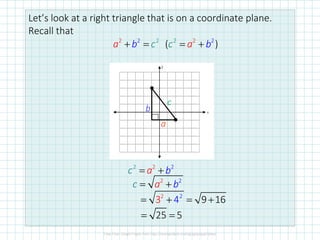
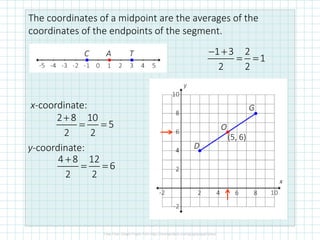
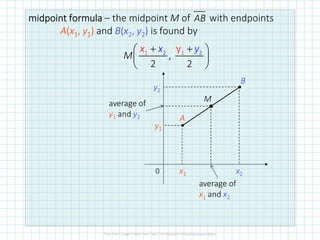
The document covers distance and midpoint formulas in coordinate geometry, enabling students to calculate the distance between points, find midpoints, and determine endpoints given midpoints. It includes examples, problems, and a sidebar discussing partitioning a segment into a specified ratio. The content is structured to facilitate learning through practice questions and illustrative examples.

1. Distance and Midpoint Formulas
The student will be able to (I can):
• Find the distance between two given points.
• Find the midpoint of two given points.
• Find the coordinates of an endpoint given one endpoint
and a midpoint.
• Find the coordinates of a point a fractional distance from
one end of a segment.

2. Let’s look at a right triangle that is on a coordinate plane.
Recall that
22 222 2
( )a b bc ac+ = = +
y
x
a
b
c
22 2
c ba= +
22
c ba= +
22
9 1643= + = +
25 5= =
●
●

3. distancedistancedistancedistance formulaformulaformulaformula – given two points (x1, y1) and (x2, y2), the
distance between them is given by
Example: Use the Distance Formula to find the distance
between F(3, 2) and G(-3, -1)
( ) ( )
2 2
12 12d x yyx= − + −
x1 y1 x2 y2
3 2 –3 –1
( ) ( )
2 2
3 3 1 2FG = − − + − −
( ) ( )
2 2
6 3 36 9= − + − = +
45 3 5= =
Remember that the square of a negative number is
positivepositivepositivepositive.

4. Problems 1. Find the distance between (9, –1) and
(6, 3).
A. 5
B. 25
C. 7
D. 13

5. Problems 1. Find the distance between (9, –1) and
(6, 3).
A. 5
B. 25
C. 7
D. 13
( ) ( )( )
22
6 9 3 1d = − + − −
( )
2 2
3 4 25 5= − + = =

6. Problems 2. Point R is at (10, 15) and point S is at (6,
20). What is the distance RS?
A. 1
B.
C. 41
D. 6.5
41

7. Problems 2. Point R is at (10, 15) and point S is at (6,
20). What is the distance RS?
A. 1
B.
C. 41
D. 6.5
41
( ) ( )
2 2
6 10 20 15d = − + −
( )
2 2
4 5 41= − + =

8. The coordinates of a midpoint are the averages of the
coordinates of the endpoints of the segment.
1 3 2
1
2 2
− +
= =C A T
(5, 6)
D
O
Gx-coordinate:
y-coordinate:
2 8 10
5
2 2
+
= =
4 8 12
6
2 2
+
= =

9. midpoint formulamidpoint formulamidpoint formulamidpoint formula – the midpoint M of with endpoints
A(x1, y1) and B(x2, y2) is found by
AB
1 12 2
,
2
y
2
x
M
x y+ + 
 
 
0
A
B
x1 x2
y1
y2
●
M
average of
x1 and x2
average of
y1 and y2

10. Example Find the midpoint of QR for Q(–3, 6) and
R(7, –4)
x1 y1 x2 y2
Q(–3, 6) R(7, –4)
21 3 7 4
2
2 2 2
xx + +
=
−
= =
21 2
1
2 2 2
6 4yy + +
=
−
= =
M(2, 1)

11. Problems 1. What is the midpoint of the segment
joining (8, 3) and (2, 7)?
A. (10, 10)
B. (5, –2)
C. (5, 5)
D. (4, 1.5)

12. Problems 1. What is the midpoint of the segment
joining (8, 3) and (2, 7)?
A. (10, 10)
B. (5, –2)
C. (5, 5)
D. (4, 1.5)
8 2 10
5
2 2
+
= =
3 7 10
5
2 2
+
= =

13. Problems 2. What is the midpoint of the segment
joining (–4, 2) and (6, –8)?
A. (–5, 5)
B. (1, –3)
C. (2, –6)
D. (–1, 3)

14. Problems 2. What is the midpoint of the segment
joining (–4, 2) and (6, –8)?
A. (–5, 5)
B. (1, –3)
C. (2, –6)
D. (–1, 3)
4 6 2
1
2 2
− +
= =

15. Sidebar:Sidebar:Sidebar:Sidebar:
If you are given an endpoint and a midpoint, you will then
need to find the other endpoint. While you can use the
midpoint formula and Algebra to find the missing
coordinates, I find it much easier to take advantage of the
definition – the distance between each should be the same.
Example: If one endpoint is at (1, 7) and the midpoint is at
(6, 3), what are the coordinates of the other endpoint?
(11, –1)
1 7
5 4
6 3
 
+ − 
 
6 3
5 4
11 -1
 
+ − 
 

16. Problem 3. Point M(7, –1) is the midpoint of ,
where A is at (14, 4). Find the
coordinates of point B.
A. (7, 2)
B. (–14, –4)
C. (0, –6)
D. (10.5, 1.5)
AB

17. Problem 3. Point M(7, –1) is the midpoint of ,
where A is at (14, 4). Find the
coordinates of point B.
A. (7, 2)
B. (–14, –4)
C. (0, –6)
D. (10.5, 1.5)
AB
14 4
7 5
7 1
 
− − 
− 
7 1
7 5
0 6
− 
− − 
 −

18. partitioning a segmentpartitioning a segmentpartitioning a segmentpartitioning a segment – dividing a segment into two pieces
whose lengths fit a given ratio.
For a line segment with endpoints (x1, y1) and (x2, y2), to
partition in the ratio b : a,
Example: has endpoints Q(–3, –16) and R(15, –4). Find
the coordinates of P that partition the segment in
the ratio 1 : 2.
QR
1 2 1 2
,
b ba a
a ab b
x x y y + +    + +
( ) ( ) ( ) ( )1 13 15 16 4
,
2
1 1
2
2 2
P
 − + − + −     + + 
( )3, 12P −