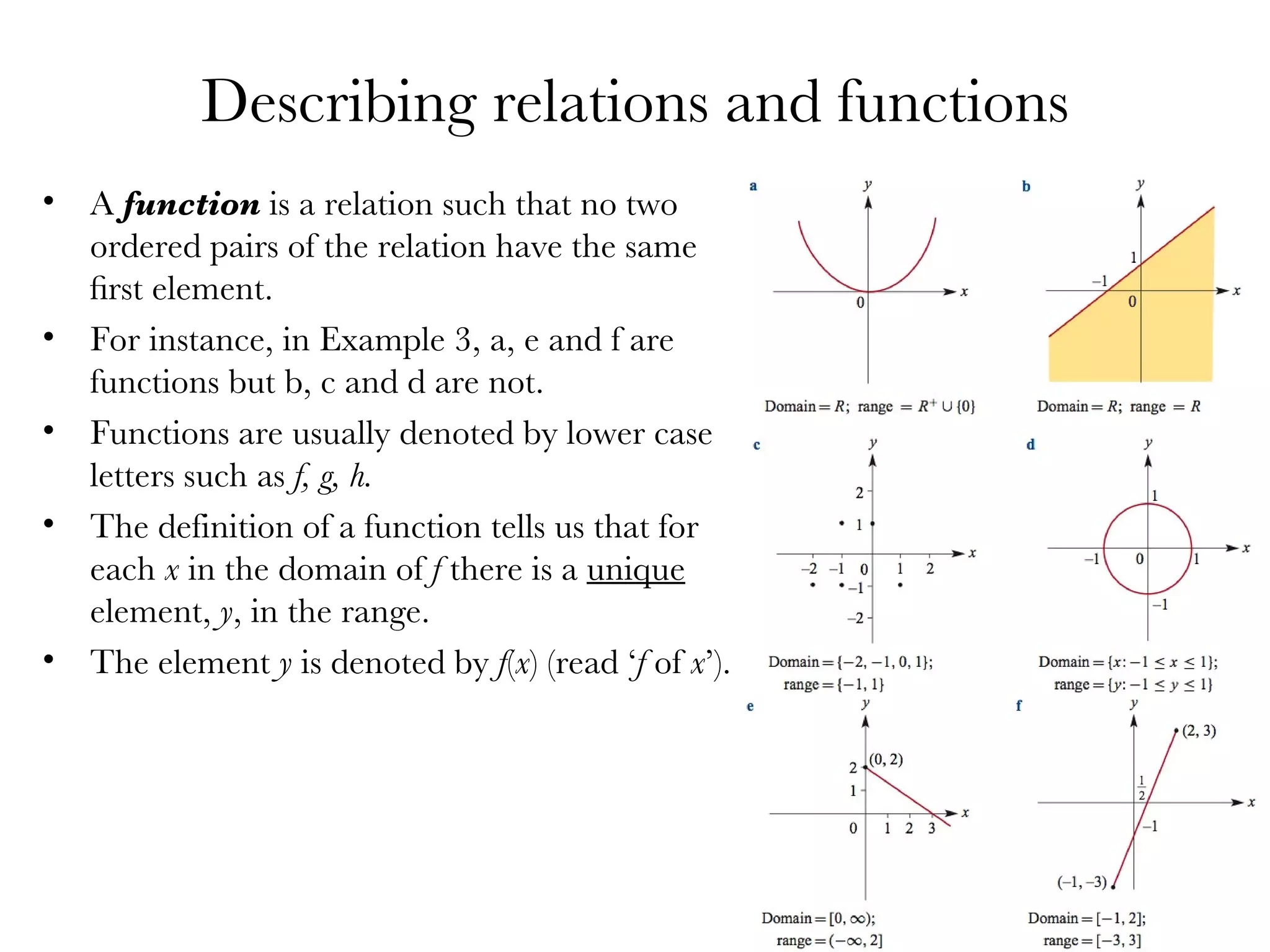
The document defines key concepts related to functions and relations, including: - Sets, set notation, and operations like intersection and union - Different types of number sets like natural, integer, rational, and real numbers - Ordered pairs and how they are used to define relations and functions - The domain and range of relations and functions - What defines a function versus a relation - Examples of functions, their graphs, and evaluating functions for given inputs

1. Functions and Relations Objectives To understand and use the notation of sets, including the symbols ∈, ⊆, ∩, ∪, ∅ and \. To use the notation for sets of numbers. To understand the concept of relation. To understand the terms domain and range. To understand the concept of function. To understand the term one-to-one. To understand the terms implied domain, restriction of a function, hybrid function, and odd and even functions. To understand the modulus function. To understand and use sums and products of functions. To define composite functions. To understand and find inverse functions. To apply a knowledge of functions to solving problems.

2. Set Notation A set is a collection of objects e.g A = {3,4}. The objects in the set are known as the elements or members of the set. For example, you are ‘elements’ of our class ‘set’. 3 ∈ A means ‘3 is a member of set A ’ or ‘3 belongs to A ’. 6 ∉ A means ‘6 is not an element of A’ .

3. Set Notation If x ∈ B implies x ∈ A, then B is a subset of A , we write B ⊆ A . This expression can also be read as ‘ B is contained in A ’ or ‘ A contains B ’. The set ∅ is called the empty set or null set. A ∩ B is called the i n tersection of A and B . Thus x ∈ A ∩ B if and only if x ∈ A and x ∈ B . A ∩ B = ∅ if the sets A and B have no elements in common. A ∪ B , is the u nion of A and B. If elements are in both A and B they are only included in the union once. The set difference of two sets A and B is denoted A \ B ( A but not B ) Example 1 : A = {1, 2, 3, 7}; B = {3, 4, 5, 6, 7} Find: a) A ∩ B b) A ∪ B c) A \ B d) B \ A Solution: a) A ∩ B = {3, 7} b) A ∪ B = {1, 2, 3, 4, 5, 6, 7} c) A \ B = {1, 2} d) B \ A = {4, 5, 6}

4. Sets of numbers N: Natural numbers {1, 2, 3, 4, . . .} Z: Integers {. . . ,−2,−1, 0, 1, 2, . . .} Q: Rational numbers – can be written as a fraction. Each rational number may be written as a terminating or recurring decimal. The real numbers that are not rational numbers are called irrational (e.g. π and √2). R: Real numbers. (How can a number not be real?) It is clear that N ⊆ Z ⊆ Q ⊆ R and this may be represented by the diagram:

5. Sets of numbers The following are also subsets of the real numbers for which there are special notations: R + = { x : x > 0} R − = { x : x < 0} R \{0} is the set of real numbers excluding 0. Z + = { x : x ∈ Z, x > 0} Note: { x : 0 < x < 1} is the set of all real numbers between 0 and 1. { x : x > 0 , x rational} is the set of all positive rational numbers . {2 n : n = 0, 1, 2, . . .} is the set of all even numbers.

6. Representing sets of numbers on a number line Among the most important subsets of R are the intervals. (-2, 4) means all ‘real’ numbers between (but not including) -2 and 4. [3, 7] means all ‘real’ numbers between 3 and 7 inclusive. [4, ∞) means all ‘real’ numbers greater than or equal to 4. (-∞, 3) means all ‘real’ numbers less than 3.

7. Representing sets of numbers on a number line Example 2: Illustrate each of the following intervals of the real numbers on a number line: a [−2, 3] b (−3, 4] c (−∞, 5] d (−2, 4) e (−3,∞)

8. Describing relations and functions An ordered pair , denoted ( x, y ), is a pair of elements x and y in which x is considered to be the first element and y the second (it doesn’t mean they have to be in numerical order). A relation is a set of ordered pairs. The following are examples of relations: S = {(1, 1), (1, 2), (3, 4), (5, 6)} T = {(−3, 5), (4, 12), (5, 12), (7,−6)} The domain of a relation S is the set of all first elements of the ordered pairs in S. The range of a relation S is the set of all second elements of the ordered pairs in S. In the above examples: domain of S = {1, 3, 5}; range of S = {1, 2, 4, 6} domain of T = {−3, 4, 5, 7}; range of T = {5, 12, −6} A relation may be defined by a rule which pairs the elements in its domain and range. Let’s watch an example.

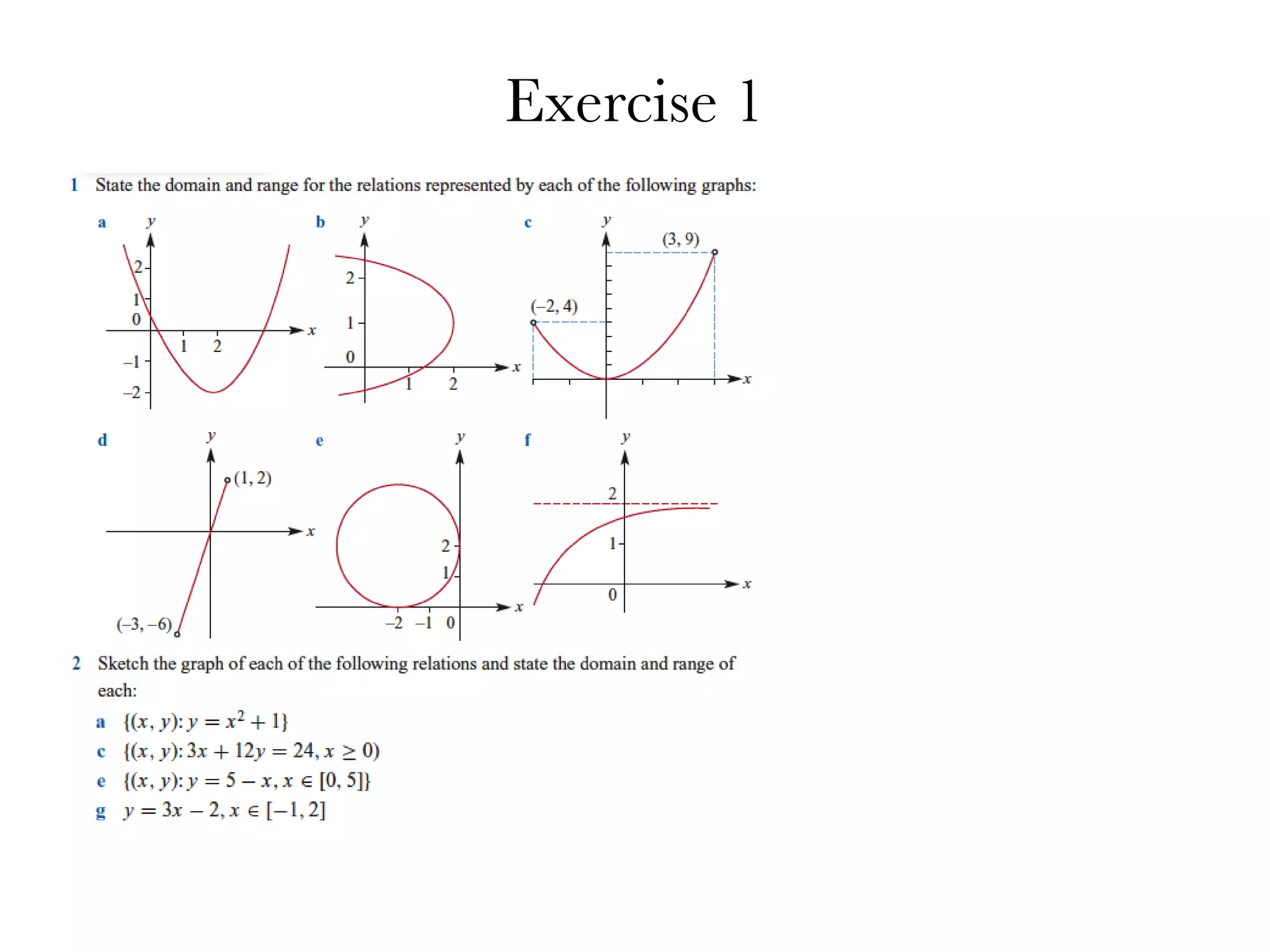
9. Describing relations and functions Example 3: Sketch the graph of each of the following relations and state the domain and range of each. a {( x, y ): y = x 2 } b {( x, y ): y ≤ x + 1} c {(−2 , −1) , (−1 , −1) , (−1 , 1) , (0 , 1) , (1 , −1)} d {( x, y ): x 2 + y 2 = 1} e {( x, y ): 2 x + 3 y = 6 , x ≥ 0} f {( x, y ): y = 2 x − 1 , x ∈ [−1 , 2]}

10. Describing relations and functions A function is a relation such that no two ordered pairs of the relation have the same first element. For instance, in Example 3, a, e and f are functions but b, c and d are not. Functions are usually denoted by lower case letters such as f, g, h. The definition of a function tells us that for each x in the domain of f there is a unique element, y , in the range. The element y is denoted by f ( x ) (read ‘ f of x ’).

11. Describing relations and functions Example 4: If f ( x ) = 2 x 2 + x, find f (3) , f (−2) and f ( x − 1) . Solution f (3) = 2(3) 2 + 3 = 21 f (−2) = 2(−2) 2 − 2 = 6 f ( x − 1) = 2( x − 1) 2 + x − 1 = 2( x 2 − 2 x + 1) + ( x − 1) = 2 x 2 − 3 x + 1

12. Describing relations and functions Example 5: For each of the following, sketch the graph and state the range: a f : [−2 , 4] -> R, f ( x ) = 2 x − 4 b g : (−1 , 2] -> R, g ( x ) = x 2

13. Exercise 1

14. Exercise 1