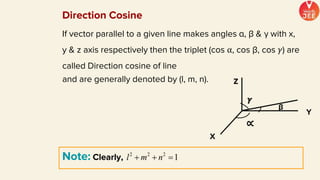
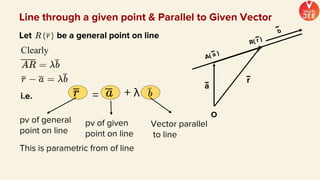
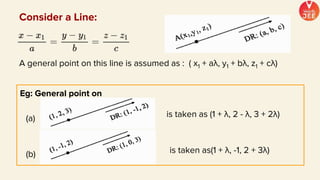
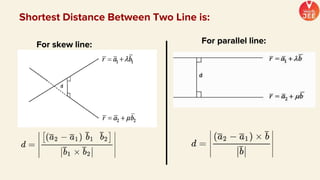
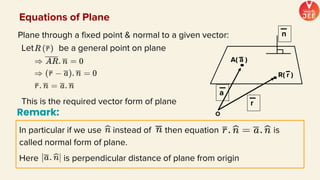
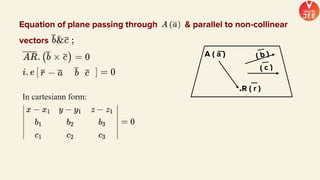
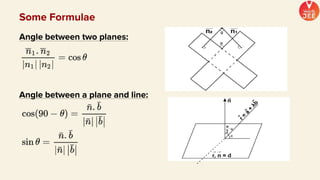
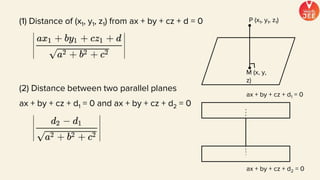
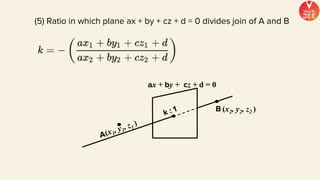
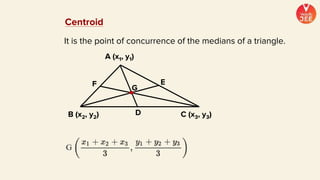
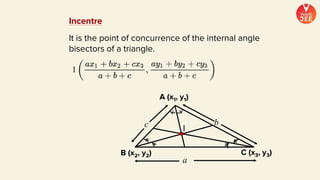
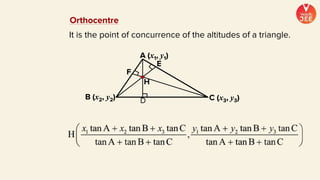
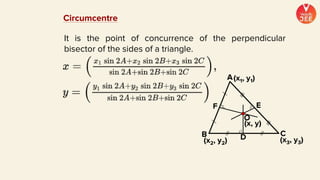
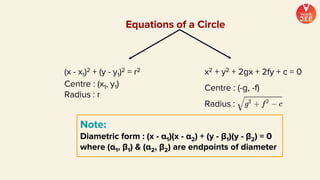
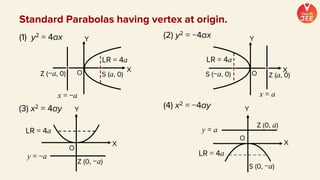
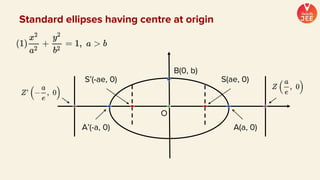
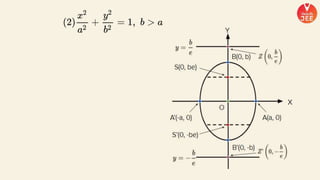
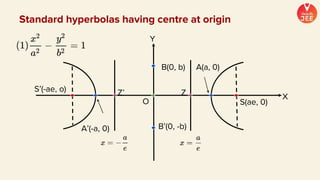
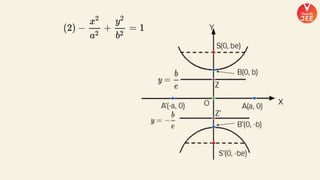
(1) The document discusses various topics in geometry including lines, circles, triangles, and coordinate geometry. Key concepts discussed include the centroid, orthocentre, and circumcentre of a triangle as well as equations of lines and circles.
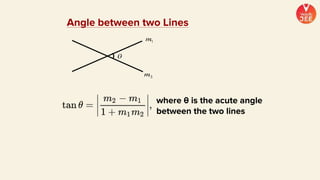
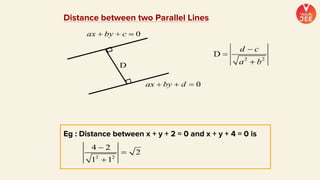
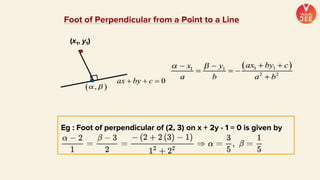
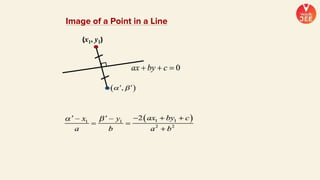
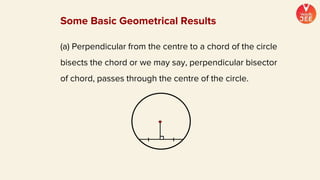
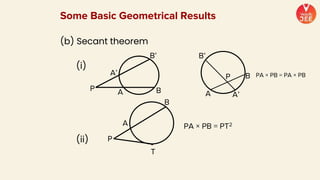
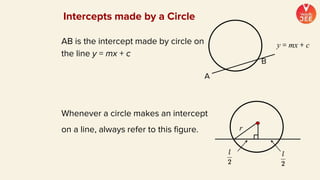
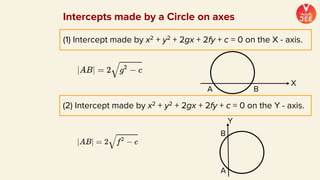
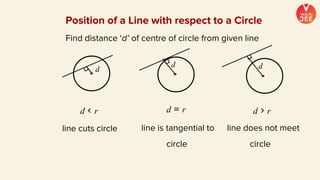
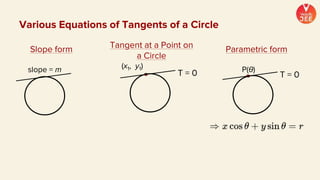
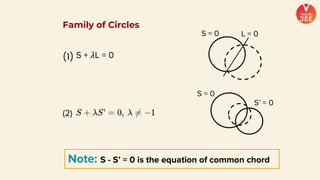
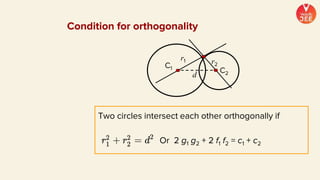
(2) Formulas are provided for distances between points and lines, parallel lines, perpendiculars from points to lines, and images of points in lines. Theorems regarding secants and intercepts made by circles on lines are also summarized.
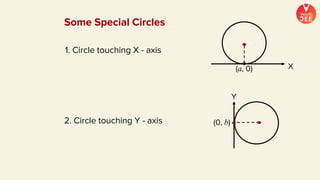
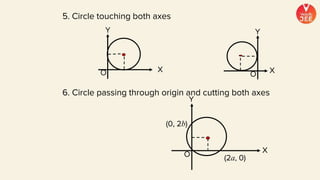
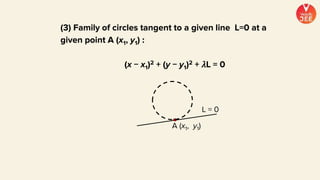
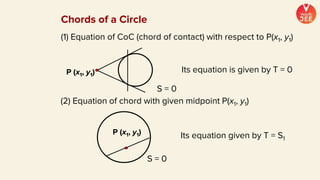
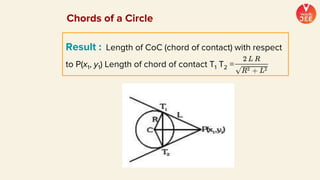
(3) Standard notations used for circles are defined, such as representing the value of the equation of a circle at a point (x1, y1) as S1. Special cases of circles like those touching or passing through










![Note for argument (or amplitude):
● If θ is argument of z then 2n𝜋 + θ ; where n is integer, is also
an argument
● The value of argument which lies in (-𝜋, 𝜋] is called principal
value of argument or amplitude .
● Argument of purely imaginary number is
● Argument of purely real number is 0 or 𝜋
● If z = 0 then arg(z) is not defined.](https://image.slidesharecdn.com/lastminuterevisionfinal11-221120131124-a5e55f26/85/Last-minute-revision-Final-1-1-pptx-12-320.jpg)






















































































![Whenever the function under consideration has one of the
following traits, always check RHL & LHL for existence of
limit.
(a) It has , [.], {.} or mod
(b) Its piecewise defined
(c) It has and
Note:](https://image.slidesharecdn.com/lastminuterevisionfinal11-221120131124-a5e55f26/85/Last-minute-revision-Final-1-1-pptx-130-320.jpg)
![Try to observe
(a) is ______; here [.] ⟶ GIF
(b) is ______; here [.] ⟶ GIF
(c) is ______; here [.] ⟶ GIF
(d) is ______; here {.} ⟶ FPF](https://image.slidesharecdn.com/lastminuterevisionfinal11-221120131124-a5e55f26/85/Last-minute-revision-Final-1-1-pptx-131-320.jpg)







![Mean value Theorems
Rolle’s theorem
If y = f(x) is a function such that:
(i) its continuous in [a, b]
(ii) its differentiable in (a, b)
(iii) f(a) = f(b)
then there exists c ∈ (a, b) such that f’(c) = 0 i.e., f’(x) = 0 has at least
one root in (a, b)](https://image.slidesharecdn.com/lastminuterevisionfinal11-221120131124-a5e55f26/85/Last-minute-revision-Final-1-1-pptx-141-320.jpg)
![Lagrange Mean value theorem
If a function y = f(x) satisfies
(i) f(x) is continuous in [a, b]
(ii) f(x) is differentiable in (a, b)
Then there exist such that](https://image.slidesharecdn.com/lastminuterevisionfinal11-221120131124-a5e55f26/85/Last-minute-revision-Final-1-1-pptx-142-320.jpg)
![Definition:
f(x) is said to be strictly increasing over an interval [a, b] if:
x2 > x1 ⇒ f(x2) > f(x1), ∀ x1, x2 ∈ [a, b]
While it is said to be increasing (or non-decreasing) if:
x2 > x1 ⇒ f(x2) ≥ f(x1), ∀ x1, x2 ∈ [a, b]
Increasing and Decreasing functions](https://image.slidesharecdn.com/lastminuterevisionfinal11-221120131124-a5e55f26/85/Last-minute-revision-Final-1-1-pptx-143-320.jpg)

![Note:
(i) f(x) is monotonic in [a, c]
(ii) f(x) is not monotonic in [a, b]
(iii) f(x) is monotonic in [c, b]
(iv) f(x) is not monotonic in neighbourhood of x = c](https://image.slidesharecdn.com/lastminuterevisionfinal11-221120131124-a5e55f26/85/Last-minute-revision-Final-1-1-pptx-145-320.jpg)













![Second Fundamental Theorem of Calculus
Let f (x) be a continuous function defined in [a, b]
If F(x) is an anti-derivative or primitive of f (x), then
This is called the Second Fundamental Theorem of Calculus.
Remark
If f(x) is discontinuous at x = c, where a < c < b, then, we have
to write](https://image.slidesharecdn.com/lastminuterevisionfinal11-221120131124-a5e55f26/85/Last-minute-revision-Final-1-1-pptx-159-320.jpg)