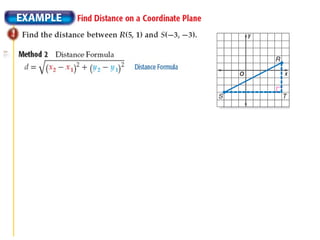
1) The document discusses distance and midpoints between two points in coordinate geometry. It defines the distance formula as the absolute value of x2 - x1 plus y2 - y1. 2) It presents the midpoint formulas, where the x-coordinate of the midpoint is (x1 + x2)/2 and the y-coordinate is (y1 + y2)/2. 3) Examples are given to find the distance between two points, and to determine the midpoint or endpoints of a line segment given coordinates of two points.

1. Notes #3 (1.3)Notes #3 (1.3)
1-3 Distance and Midpoints1-3 Distance and Midpoints
Standard 17.0Standard 17.0 Students proveStudents prove
theorems using coordinate geometrytheorems using coordinate geometry
including the midpoint of a line segment,including the midpoint of a line segment,
and the distance formula midpointand the distance formula midpoint
Objective:Objective: Find the distance betweenFind the distance between
two points and the midpoint of atwo points and the midpoint of a
segment.segment.

2. Number LineNumber Line
The distance between P and Q is written
PQ = |b – a| or |a – b|
a b
P Q

3. 2)
12
(2)
12
( yyxxd −+−=
 The distance d between two points (xThe distance d between two points (x11,y,y11) and (x) and (x22,y,y22) is) is
given bygiven by
The Distance FormulaThe Distance Formula
A(x1, y1)
B(x2, y2)

6. Midpoint FormulasMidpoint Formulas
 The midpoint of a segment is the point on the segmentThe midpoint of a segment is the point on the segment
that divides the segment into two congruent segmentsthat divides the segment into two congruent segments
Number LineNumber Line Coordinate PlaneCoordinate Plane







 ++
=
2
,
2
2121 yyxx
M
2
ba
M
+
=
a and b are the endpoints x1, y1, x2, and y2 are
coordinate points on the graph

7. ExampleExample
Find the coordinate of
the midpoint of PQ, where
P is -20 and Q is 40
Find the coordinate of
the midpoint of JK, where
J(-1,2) and K(6, 1)

8. ExampleExample
Find the coordinates of the endpoint X if Y(-1,6) is
the midpoint of XZ and Z (2,8)