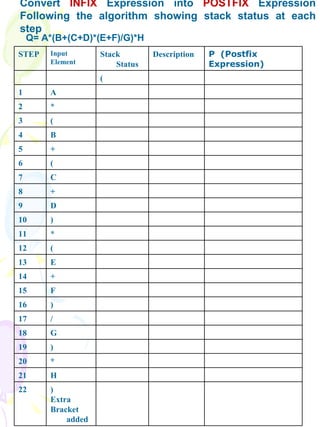
Stacks have several application areas including: 1) When functions are called to save return addresses and local variables. 2) To convert infix expressions to postfix form by acting as a placeholder. 3) To evaluate postfix expressions by holding operands and intermediate results.

1. Stacks Application Areas of Stacks

2. When functions are called. To convert a infix expression to postfix. To evaluate a postfix expression. Stacks are used : Application Areas of Stacks

3. Algorithm to convert INFIX to POSTFIX expression

4. Postfix Expression involving LOGICAL OPERATORS/CONSTANTS LOGICAL OPERATORS NOT : Complementation (Unary Operator) (HIGHEST PRIORITY) Result is TRUE if operand is FALSE and vice versa. AND : Logical multiplication (PRIORITY LESS THAN NOT Result is TRUE if both operands are TRUE otherwise FALSE hi OR : Logical Addition (LOWEST PRIORITY) Result is FALSE if both operands are FALSE otherwise TRUE LOGICAL CONSTANTS YES / TRUE NO / FALSE Just For Reference

5. Q= A*(B+(C+D)*(E+F)/G)*H Convert INFIX Expression into POSTFIX Expression Following the algorithm showing stack status at each step ) Extra Bracket added 22 H 21 * 20 ) 19 G 18 / 17 ) 16 F 15 + 14 E 13 ( 12 * 11 ) 10 D 9 + 8 C 7 ( 6 + 5 B 4 ( 3 * 2 A 1 ( P (Postfix Expression) Description Stack Status Input Element STEP

6. Evaluation of POSTFIX Expression Postfix Expression is without parenthesis. Postfix Expression has only Operands and Operators Stack is used to hold operand/intermediate results (STACK APPLICATION) Expression Evaluated from left to right Some points to remember regarding POSTFIX expressions:

7. Evaluation of POSTFIX Expression (Algorithm) Let P be the expression in POSTFIX notation Expression is Evaluated from left to right Add ; at the end to mark end of expression P Scan the postfix expression from left to right taking one element at a time While (element !=‘;’) repeat the steps 2.1 and 2.2 2.1 if (element = Operand ) it is PUSHed in STACK 2.2 If (element == Operator ) { POP first element from TOP call it A POP second element from TOP call it B Perform OPERATION B operator A PUSH Result in STACK } Pop the value from stack TOP which is result of the expression { {

8. Assignment Stack Applications

9. post fix , infix notation (2 marks) Give postfix form of the following expression: (i) A*(B+(C+D)*(E+F)/G)*H (ii) A+[(B+C)*(D+E)*F]/G (iii) A*(B+D)/E-F-(G+H/K) (iv) ((A-B)*(D/E))/(F*G*H) (v) (True && false) || !(false||true)

10. post fix , infix notation (2 marks) Evaluate the following postfix expression using a stack and show the Contents of stack after each step: (i) 50,40,+, 18,14,-,4,*,+ (ii) 100,40,8,+,20,10,-,+,* (iii) 5,6,9,+,80,5,*,-,/ (iv) 120,45,20,+,25,15,-,+,* (v) 20,45,+,20,10,-,15,+,* (vi) TRUE,FALSE, TRUE FALSE, NOT, OR, TRUE , OR,OR,AND

11. post fix , infix notation (2 marks) 3. Write the equivalent infix expression for : i. 10,3,*,7,1,-,*,23,+ ii. /+a*bc-c*db iii. abc*+cdb*-/

12. The End