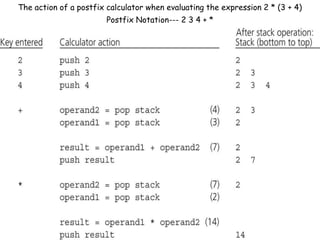
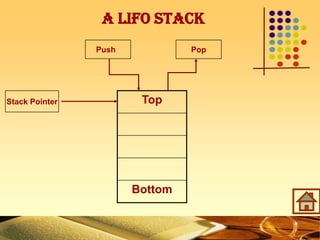
This document discusses stacks as a data structure. It defines a stack as a Last In First Out (LIFO) structure where newly added items are placed on top. The core stack operations of push, pop, and peek are described. An array implementation of a stack is presented, along with applications like checking for balanced braces, converting infix to postfix notation, and a postfix calculator. Pseudocode provides an algorithm for infix to postfix conversion using a stack.

1. A
Data Structure

2.  What is a Stack
 Stack Operations
 LIFO Stack
 Animation Depicting Push Operation
 Animation Depicting Pop Operation
 Array Implementation of Stack
 Applications of stack
Checking for balanced braces
Converting Infix Expression to Postfix
Postfix calculator

3. What is a Stack?
A stack is a Last In, First Out (LIFO) data
structure,objects inserted last are the first to
come out of the stack
Anything added to the stack goes on the “top”
of the stack
Anything removed from the stack is taken from
the “top” of the stack
Things are removed in the reverse order from
that in which they were inserted

4. Stack Operations
 PUSH
Adds the object to the top of the stack
 POP
Removes the object at the top of the stack
and returns it
 PEEK
Returns the top object of the stack but does
not remove it from the stack
 ISEMPTY
Returns True if Stack is empty

5. A LIFO Stack
Top
Bottom
Stack Pointer
Push Pop

8. array Implementation of Stack
A[1] A[2] …. …. …. A[n]
w y
Pop
Stack pointer
J=n
Stack Full
Stack pointer
J=2
Before Push
Stack pointer
J=3
After Push
After many
Push Ops
Push X w y x
Stack Pointer
J=0
Stack Empty
After many Pop ops
Stack Pointer
J=3
Before Pop
Stack Pointer
J=2
After Pop

9. Checking for Balanced Braces
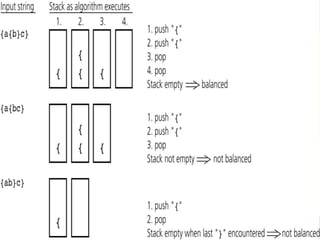
 ([]({()}[()])) is balanced; ([]({()}[())]) is not
 Simple counting is not enough to check
balance
 You can do it with a stack: going left to
right,
 If you see a (, [, or {, push it on the
stack
 If you see a ), ], or }, pop the stack
and check whether you got the
corresponding (, [, or {
 When you reach the end, check that the
stack is empty

11. Converting Infix Expressions to Equivalent
Postfix Expressions
 Infix Expression a+b
 Postfix Expression ab+
 An infix expression can be evaluated by first
being converted into an equivalent postfix
expression
 Facts about converting from infix to postfix
 Operands always stay in the same order with
respect to one another
 All parentheses are removed

12. Algorithm : Converting Infix Expression to
Postfix using stack
Suppose X is an arithmetic expression written in infix notation.
This algorithm finds the equivalent postfix expression Y.
1. Push "(" onto STACK, and add ")" to the end of X.
2. Scan X from left to right and REPEAT Steps 3 to 6 for each element of X UNTIL the
STACK is empty :
3. If an operand is encountered, add it to Y.
4. If a left parenthesis is encountered, push it onto STACK.
5. If an operator is encountered, then :
(a) Repeatedly pop from STACK and add to Y each operator (on the top of STACK) which has
the same precedence as or higher precedence than operator.
(b) Add operator to STACK.
/* End of If structure * /
6. If a right parenthesis is encountered, then :
(a) Repeatedly pop from STACK and add to Y each operator (on the top of STACK)
until a left parenthesis is encountered.
(b) Remove the left parenthesis. [Do not add the left parenthesis to Y].
/* End of If structure * /
/* End of Step 2 loop * /
7. END.

13. A trace of the algorithm that converts the infix expression
a - (b + c * d)/e to postfix form

14. A postfix calculator
 When an operand is entered, the calculator
 Pushes it onto a stack
 When an operator is entered, the calculator
 Applies it to the top (one or two, depending
on unary or binary operator) operand(s) of
the stack
 Pops the operands from the stack
 Pushes the result of the operation on the
stack

15. The action of a postfix calculator when evaluating the expression 2 * (3 + 4)
Postfix Notation--- 2 3 4 + *

16. Acknowledgement
 Data Structures BY Tanenbaum
 Internet
 Computer Science C++ A textbook for class XII -By
Sumita Arora
prepared by-
Seema kaushik,
Computer science department,
DAV public school, sector-14, gurgaon