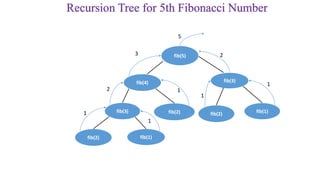
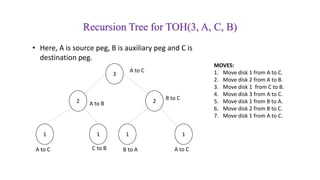
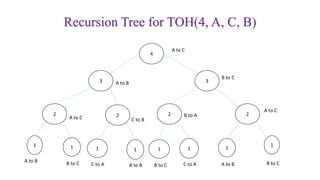
The document discusses the concept of stacks, detailing their operations such as push and pop, and the conditions for overflow and underflow. It also explains infix, prefix, and postfix notations for arithmetic expressions and includes algorithms for converting between these notations. Additionally, it provides examples of stack implementation in C, as well as exercises to reinforce the concepts presented.

1. Stack
1
BSc CSIT
Tribhuvan University Kathmandu
By:
Dabal Singh Mahara
2017

2. Unit – 3
Contents Hours Marks
a. Concept and Definition
• Primitive Operations
• Stack as an ADT
• Implementing PUSH and POP operation
• Testing for overflow and underflow conditions
b. The Infix, Postfix and Prefix
• Concept and Definition
• Converting from infix to postfix
• Evaluating the postfix operation
c. Recursion
• Concept and Definition
• Implementation of :
 multiplication of Natural Numbers
 Factorial
 Fibonacci Sequences
 The Tower of Hanoi
2
3
3
11
2

3. Concept and Definition
of Stack

4. 4
What is a Stack?
• A stack is a data structure in which insertions and deletions can only be
done at one end, called the top.
• The Insertion operation is referred to as Push and deletion operation is
called POP.
• As all the insertions or deletions are done at top of the stack, the last item
pushed into the stack is always the first item to be popped from the stack.
So, the stack is also called as a Last In, First Out or a LIFO structure.
• The stack is said to be in underflow condition if it contains no elements.
• It is in overflow condition if the stack is full. That is, no element can be
added to it.
• A common example of a stack, which permits the selection of only its end
elements, is a stack of books. A person desiring a book can pick up only the
book at the top.

5. Addition of data into the stack
2
4
6top
Push 8 top
2
4
6
8
Push 10
top
2
4
6
8
10
Increment the
top

6. Deletion of data from the stack
2
4
6
top
8
10
Pop top
2
4
6
8
Pop top
2
4
6
Decrement the top

7. Applications of Stack
Stack is used directly and indirectly in the following fields:
• To evaluate the expressions (postfix, prefix)
• To keep the page-visited history in a Web browser
• To perform the undo sequence in a text editor
• To implement recursion or function to hold status of calling and called
functions
• To check syntax in parser
• To store level wise information for backtracking algorithm
7

8. 8
Operations on Stacks
The PUSH and POP operations are the primitive operations on a stack.
Some of the typical operations performed on stacks are:
• create (s) – to create s as an empty stack
• push (s, i) – to insert the element i on top of the stack s
• pop (s) – to remove the top element of the stack and
to return the removed element as a function value.
• top (s) – to return the top element of stack(s)
• Isempty(s) – to check whether the stack is empty or not. It returns true if the
stack is empty, and returns false otherwise.
• IsFull (s) - The isfull operation is used to check whether the stack is full or
not ( i.e. stack overflow)

9. The Stack ADT
• A stack S of type T is a finite sequence of elements of of type T on which
following operations are defined:
• CreateEmptyStack(S): Create or make stack S be an empty stack
• Push(S, x): Insert x at one end of the stack, called its top
• Top(S): If stack S is not empty; then retrieve the element at its top
• Pop(S): If stack S is not empty; then delete the element at its top
• IsFull(S): Determine if S is full or not. Return true if S is full stack; return
false otherwise
• IsEmpty(S): Determine if S is empty or not. Return true if S is an empty
stack; return false otherwise.
9

10. Implementation of Stack
• Stack can be implemented in two ways:
1. Array Implementation of stack (or static implementation)
2. Linked list implementation of stack (or dynamic)
• Array (static) implementation of a stack:
o This implementation uses a one dimensional array to store the data and top
of stack is an integer value (an index of an array) that indicates the top
position of a stack.
o Each time data is added or removed, top is incremented or decremented
accordingly, to keep track of current top of the stack.
o By convention, in C implementation the empty stack is indicated by setting
the value of top to -1.

11. Array Implementation of Stack
11
#define MAX 10
struct stack
{
int items[MAX]; //Declaring an array to store items
int top; //Top of a stack
};
struct stack s; // declaration of stack variable

12. Creating Empty stack
• The value of top=-1 indicates the empty stack in C
implementation.
• /*Function to create an empty stack*/
void create_empty_stack(struct stack *s)
{
s->top = -1;
}

13. Stack Empty or Underflow
• This is the situation when the stack contains no element.
• At this point the top of stack is present at the bottom of the stack.
• In array implementation of stack, conventionally top=-1 indicates the
empty.
• The following function return 1 if the stack is empty, 0 otherwise.
int isempty(struct stack *s)
{
if(s->top == -1)
return 1;
else
return 0;
}

14. Stack Full or Overflow
• This is the situation when the stack becomes full, and no more elements
can be pushed onto the stack.
• At this point the stack top is present at the highest location (MAX - 1) of the
stack.
• The following function returns true (1) if stack is full false (0) otherwise.
int isfull(struct stack *s)
{
if(s->top==MAX-1)
return 1;
else
return 0;
}

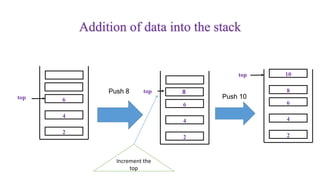
15. PUSH operation on Stack
• Let Stack[MAX] be an array to implement the stack. The variable top denotes
the top of the stack.
• Algorithm for PUSH operation:
This algorithm adds or inserts an item at the top of the stack .
1. [Check for stack overflow?]
if top=MAX-1 then
print “Stack Overflow” and Exit
else
Set top = top+1 [Increase top by 1]
Set Stack[top] = item [Inserts item in new top position]
2. Exit

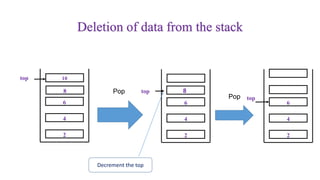
16. • POP operation: deletes the top element of the stack and assign it to a
variable item
• Algorithm:
1. [Check for the stack Underflow]
If top<0 then
Print “Stack Underflow” and Exit
else [Remove the top element]
Set item=Stack [top]
Set top=top-1 [Decrement top by 1]
Return the deleted item from the stack
2. Exit
Dabal Mahara 16
POP operation on Stack

17. The C function for push operation
void push(struct stack *s, int element)
{
if(isfull(s)) /* Checking Overflow condition */
printf("n n The stack is overflow: Stack full ! n");
else
s->items[++(s->top)]=element;
/* First increase top by 1 and store
element at top position*/
}

18. The C function for push operation
• Alternatively we can define the push function as give below:
void push()
{
int item;
if(top == MAX - 1) //Checking stack overflow
printf("n The Stack Is Full");
else
{
printf("Enter the element to be inserted");
scanf("%d",&item); //reading an item
top = top+1; //increase top by 1
stack[top] = item; //storing the item at the top of the stack
}
}

19. The C function for POP operation
void pop(struct stack *s)
{
if(isempty(s))
printf("nn stack Underflow: Empty Stack!!!");
else
printf("n The deleted item is %d:t",s->items[s->top--]);
/*deletes top element and decrease top by 1 */
}

20. • Alternate Definition
The C function for POP operation
void pop()
{
int item;
if(top ==-1) //Checking Stack Underflow
printf("The stack is Empty");
else
{
item = stack[top]; //Storing top element to item variable
top = top-1; //Decrease top by 1
printf(“The popped item is=%d”,item); //Displaying the deleted item
}
}

21. The Infix, Postfix and Prefix
Notations

22. The Infix, Prefix, Postfix Notation
Arithmetic expression:
An expression is defined as a number of operands or data items combined using
several operators. There are basically three types of notations for an expression;
1) Infix notation 2) Prefix notation 3) Postfix notation
Infix notation:
It is most common notation in which, the operator is written or placed in-between the
two operands. For eg. The expression to add two numbers A and B is written in infix
notation as, A + B
Prefix Notation:
It is also called Polish notation, named after in the honor of the mathematician Jan
Lukasiewicz, refers to the notation in which the operator is placed before the operand
as, +AB As the operator ‘+’ is placed before the operands A and B,
Postfix Notation:
In the postfix notation the operators are written after the operands, so it is called the
postfix notation (post means after), it is also known as suffix notation or reverse polish
notation. The above postfix if written in postfix notation looks like follows; AB+
22

23. Infix to Postfix Conversion
Algorithm:
Let P be a valid infix expression , Q be postfix expression , Opstack be an operator stack.
1. Make an empty String, Q for postfix expression.
2. Opstack = empty stack
3. Repeat steps 4 to 8, until end of string, P.
4. Scan one char at a time from left to right in P.
5. If scan char is '(', then push it into Opstack.
6. If scan char is operand, then append it to Postfix String Q.
7. If scan char is operator, then,
a. while(Opstack is not empty and precedence(Opstack_Top) >= precedence(scan char))
i. Pop the Opstack and append it to Postfix String Q.
b. Push the scan operator to Opstack.
8. If scan char is ')' then Pop Opstack and append to Postfix String, unitl '(' is encountered. Ignore
both '(' and ')'.
9. while( Opstack is not empty ) Pop Opstack and append to Postfix String.
10.End. 23

24. • Convert following infix expression into postfix expression:
a + b * c + ( d * e + f ) * g
• Solution,
• Scan one character at time from the input string until end of the input
• Create an empty stack 'Opstack' to hold operators and output string Q
to hold output postfix expression.
Example: infix to postfix conversion
Postfix String: Q
Opstack

25. Input String: a + b * c + ( d * e + f ) * g
• Let us start scanning the input string
• Read first symbol a, since it is operand, pass it to the poststring Q.
• Read next symbol '+' and pushed into stack.
• Read next symbol b and append it to Q.
• Read next symbol i.e. * , check precedence of stack top and scan
char push * into the stack.
• Read c from input string and append it to Q.
• Read next symbol +, check precedence with stack operators, we find that
* has higher precedence so pop * and append it to Q. Again check for next stack
symbol + which is of equal precedence with scan +, therefore, pop it and append to
the Q. Finally push scan + into the stack.
Example: infix to postfix conversion
*
+
Opstack
PostString Q: a b
PostString Q: a
PostString Q: a b c
PostString Q: a b c * +
+
Opstack

26. Input string: a + b * c + ( d * e + f ) * g
• Next symbol scanned: (, push into the stack.
• Next symbol scanned: d , append to the Q.
• Next symbol scanned: * , push into the stack because precedence of stack
top operator is lowest.
• Next scan symbol: e , append to Q.
Example: infix to postfix conversion
*
(
+
Opstack
PostString Q: a b c * + d e *

27. • Next Scan symbol: +, pop * from stack and
append it to Q. Then , push + to the stack.
• Next Scan symbol: f , add to Q.
• scan symbol: ), pop + from stack and add to Q.
Pop ( from stack and ignore it.
Example: infix to postfix conversion
+
(
+
Opstack
PostString Q: a b c * + d e * f +
+
Opstack

28. • Input string: a + b * c + ( d * e + f ) * g
• Scan symbol: * , push it into the stack.
• scan symbol: g, add it to Q.
Example: infix to postfix conversion
PostString Q: a b c * + d e * f +
*
+
Opstack
PostString Q: a b c * + d e * f + g

29. • Input string is no more left to scan, so pop Optack and append
to Q until empty.
• This is the output string in postfix notation.
Example: infix to postfix conversion
PostString Q: a b c * + d e * f + g * +
Opstack

30. Example: infix to postfix conversion
• The following tracing of the algorithm illustrates the algorithm. Consider an
infix expression : ((A-(B+C))*D)$(E+F)

31. Exercise
• Convert the following infix expression to postfix
expression
i. (A+B)*(C+D)/E-F
ii. (A*B)+(C-D)
iii. A$B*C-D+E/F/(G+H)
iv. A-B/(C*D$E)

32. Postfix Evaluation
Algorithm:
Let P be an expression written in postfix expression, Vstack be an operand stack.
1. Vstack = empty stack
2. Repeat steps 3, 4 and 5 until end of string, P.
3. Scan one char at a time from left to right in P.
4. If scan char is operand, then read its corresponding value and push it into
vstack.
5. If scan char is operator, then,
a. Pop and place into operand2.
b. Pop and place into operand1.
c. Compute : result = operand1 operator operand2
d. Push result into vstack.
6. Pop vstack and display, which is required value of given expression.
7. End.
32

33. • Evaluate: ABC+*CBA-+* where A=1, B=2, C =3.
33
Example: postfix expression Evaluation

34. Exercise
• Evaluate the postfix expression
i. AB+CD-* , Given A = 3, B = 2, C = 4 D = 2
ii. ABC+-D*EF+$ where, A=1, B=2, C=3, D=5, E=7, F=8

35. Infix to Prefix Conversion
Algorithm:
Let P be a valid infix expression , Q be prefix stack , Opstack be an operator stack.
1. Make an empty String, Q for prefix stack.
2. Opstack = empty stack
3. Repeat steps 4 to 8, until end of string, P.
4. Scan one char at a time from right to left in P.
5. If scan char is ')', then push it into Opstack.
6. If scan char is operand, then push it to Prefix stack Q.
7. If scan char is operator, then,
a. while(Opstack is not empty and precedence(Opstack_Top)> precedence(scan char))
i. Pop the Opstack and push it to Prefix stack Q.
b. Push the scan operator to Opstack.
8. If scan char is '(', then Pop Opstack and push it prefix stack , until ')' is encountered. Ignore both '(' and ')'.
9. Pop Opstack and Push it to Prefix stack until Opstack is not empty.
10.Pop and print the prefix stack to the prefix string of given infix string.
11.End. 35

36. Convert infix expression A-B/C*(C*D$E) to prefix expression.
Scan char Prefix Stack Opstack
) )
E E )
$ E )$
D ED )$
* ED$ )*
C ED$C )*
( ED$C*
* ED$C* *
C ED$C*C *
/ ED$C*C */
B ED$C*CB */
- ED$C*CB/* -
A ED$C*CB/*A -
ɸ ED$C*CB/*A -
36
• The Prefix String of given infix expression is : -A*/BC*C$DE
Example: infix to prefix conversion

37. Exercise
Trace the algorithm for the input strings:
i) A+(B/C-(D*E$F)+G)*H
ii)(A-(B/C))*((D*E)-F)

38. Prefix Evaluation
Algorithm:
Let P be an expression written in infix expression, Vstack be an operand stack.
1. Vstack = empty stack
2. Repeat steps 3, 4 and 5 until end of string, P.
3. Scan one char at a time from right to left in P.
4. If scan char is operand, then read its corresponding value and push it into
vstack.
5. If scan char is operator, then,
a. Pop and place into operand1.
b. Pop and place into operand2.
c. Compute : result = operand1 operator operand2
d. Push result into vstack.
6. Pop vstack and display, which is required value of given expression.
7. End.
38

39. 39
Example: prefix expression Evaluation
• Evaluate: +-*+12/421$42
Result of Expression = 21

40. Exercise
• Evaluate the following infix Expression:
i. +-*+AB/CBA$CB where A =1, B = 2 and C=4
ii. +-*$ ABCD//EF+GH, where A=4, B =2, C=3, D=3, E = 8,
F=4, G =1, H=1

41. Recursion
41Dabal Mahara

42. • A Definition Is Recursive If It Is Defined In Terms Of Itself
• Recursion is a process by which a function calls itself repeatedly, until some
specified condition has been satisfied.
• The process is used for repetitive computations in which each action is stated in
terms of a previous result.
• Recursion makes solving problems easier by breaking them into smaller sub
problems thereby making it easier to understand the problem. As such, not all
problems can be broken down into smaller sub problems so that they could be
solved recursively.
• The most important advantage is that recursion makes algorithm and its
implementation simple and compact. It increases programmer efficiency.
• Not all programming languages support recursion: COBOL, early FORTRAN.
• Some programming languages rely on recursion heavily: LISP, Prolog,
Scheme.
Recursion
42Dabal Mahara

43. Constructing Recursive Algorithms
• In order to solve a problem recursively, two conditions must be satisfied.
• First, the problem must be written in a recursive form,
• Second, the problem statement must include a stopping condition.
• Recursive methods/functions require:
1. One or more (non-recursive) base cases that will cause the recursion to end.
if (n == 1) return 1;
2. One or more recursive cases that operate on smaller problems and get you closer to the
base case.
return n * factorial(n-1);
• Note: The base case(s) should always be checked before the recursive call.
• Interesting fact: Any recursive algorithm can be re-written as an iterative algorithm
(loop).

44. Recursion Vs Iteration
Iteration
• It is a process of executing a statement
or a set of statements repeatedly, until
some specific condition is met.
• It uses four clear cut steps:
initialization, condition, execution and
updation.
• Any recursive problem can be solved
iteratively.
• It is more efficient in terms of memory
utilization and execution speed.
Recursion
• Recursion is the technique of defining
anything in terms of itself.
• There must be an exclusive if statement
inside the recursive functions, specifying
stopping condition. There are base case
and recursive case in recursive function.
• Not all problems have recursive solution.
• Recursion is generally a worse option to
go simple problems. It is less efficient in
terms of memory utilization and execution
speed.
Dabal Mahara 44

45. Some Recursive Definitions

46. Factorial of an Integer
• N!, for any positive integer N, is defined to be the
product of all integers between 1 and N inclusive.
• Iterative definition :
N! = N * (N-1) * (N-2) * … * 3 * 2 * 1
int factorial (int n)
{
int i, result;
result = 1;
for (i = 1; i <= n; i++)
result = result * i;
return ( result );
}
• Recursive definition:
This definition can be expressed recursively as:
N! = 1, if N = 0
= N * (N-1)! Otherwise
int factorial ( int n)
{
if (n == 0)
return (1);
else
return (n * factorial(n - 1) );
}

47. Fibonacci Sequence
• The Fibonacci sequence is named after Italian mathematician Fibonacci.
• Fibonacci sequence is a recursive sequence, obeying the simple rule that
to calculate the next term one simply sums the preceding two.
1, 1, 2, 3, 5, 8, 13, 21, 34, ...
• Recursive Definition : The Fibonacci numbers can be recursively defined by the
rule:
fib(n) = 1 if n =1 or n = 2,
= fib(n-1) + fib(n-2) otherwise

48. Fibonacci Sequence
Recursive Function
long fib(int n)
{
if ( n == 1 || n==2)
return 1;
else
return fib(n-1) + fib(n-2);
}
Iterative Fibonacci
long fib(int n)
{
long c;
int k;
long a = 1, b = 1;
for ( k = 3; k <= n; k++)
{
c = a + b;
a = b;
b = c;
}
return c;
}

49. Recursion Tree for 5th Fibonacci Number
1
1
1
1
1
2
3 2fib(5)
fib(1)fib(2)
fib(2) fib(1)fib(2)fib(3)
fib(4) fib(3)
5

50. Multiplication of Natural Numbers
Recursive Definition
• a * b = a + a + a + a +…… b times
• The result of a * b is equal to
adding a to the result of (b-1) * a ,
that is, a * b = a * ( b-1) + a
• Recursive definition:
a * b = a if b =1
= a *( b -1) + a , if b > 1.
Recursive function
int mul(int a , int b)
{
if(b==1)
return a;
else
return (a + mul(a, b-1);
}

51. Sum of Natural Numbers
Recursive Definition
• Sum(n) = 1 + 2 + 3 + 4 +…… + n
• Recursive definition:
sum(n) = 1 if n =1
= n + sum(n-1), if n > 1.
Recursive Function
int sum(int n)
{
if(n ==1)
return 1 ;
else
return (n + sum(n-1);
}

52. X raised to Power n
Recursive Definition
• Recursive definition
XN = 1 if N = 0
= X * X(N-1) otherwise
• double power(double number, int exponent)
{
if (exponent == 0)
return (1);
return (number * power(number, exponent-1));
}
Iterative definition
• XN = X * X *X ….. * X (N factors)
• double power(double number, int exponent)
{
double p = 1;
for (int i = 1; i <= exponent; i++)
p = p * p;
return (p);
}

53. Towers of Hanoi
• The Towers of Hanoi is a puzzle made up of three vertical pegs named as
source, auxiliary and destination.
• The source peg contains n disks with varying diameter such that the largest
disk on the bottom with increasingly smaller ones on top.
• The goal is to move all of the disks from source peg to destination peg under
the following rules:
i. We can move only one disk at a time
ii. We cannot move a larger disk on top of a smaller one
iii. Each disk must always be placed on one of the pegs.

54. Tower of Hanoi Algorithm
Let’s call the three peg Src(Source), Aux(Auxiliary) and Dst(Destination).
1) IF N =1 Then
Move the single disk from Src to Dst and return
2) Else
i. Move the top N – 1 disks from the Source 'Src' to Auxiliary tower 'Aux'
ii. Move the Nth disk from Source 'Src'to Destination tower 'Dst'
iii. Move the N – 1 disks from Auxiliary tower 'Aux' to Destination tower 'Dst'.
3) End
Note: Transferring the top N – 1 disks from Source to Auxiliary tower can again be thought
of as a fresh problem and can be solved in the same manner.

55. Recursion Tree for TOH(3, A, C, B)
3
2 2
1111
A to C
B to C
A to B
A to CB to AC to BA to C
MOVES:
1. Move disk 1 from A to C.
2. Move disk 2 from A to B.
3. Move disk 1 from C to B.
4. Move disk 3 from A to C.
5. Move disk 1 from B to A.
6. Move disk 2 from B to C.
7. Move disk 1 from A to C.
• Here, A is source peg, B is auxiliary peg and C is
destination peg.

56. Recursion Tree for TOH(4, A, C, B)
4
3 3
2222
A to C
B to C
A to B
A to C
B to A
C to BA to C
11
1 11 1 1
1
B to CA to BC to AB to CA to BC to AB to CA to B

57. Moves for TOH(4, A, C, B)
1. Move disk 1 from A to B.
2. Move disk 2 from A to C.
3. Move disk 1 from B to C.
4. Move disk 3 from A to B.
5. Move disk 1 from C to A.
6. Move disk 2 from C to B.
7. Move disk 1 from A to B.
8. Move disk 4 from A to C.
9. Move disk 1 from B to C.
10. Move disk 2 from B to A
11. Move disk 1 from C to A.
12. Move disk 3 from B to C.
13. Move disk 1 from A to B.
14. Move disk 2 from A to C.
15. Move disk 1 from B to C.

58. Program: TOH
#include <stdio.h>
#include <conio.h>
void TOH(int, char, char, char);
void main()
{
int n;
printf("Enter the number of disks");
scanf("%d",&n);
printf("n The sequence of moves in TOH are:n");
toh(n,'A','C','B');
printf("nn");
system("pause");
return 0;
}
void toh(int n, char frompeg, char topeg, char auxpeg )
{
if (n==1)
{
printf("n Move disk %d from peg %c to peg %c",n,frompeg,topeg);
}
else
{
toh(n-1,frompeg,auxpeg,topeg);
printf("n move disk %d from peg %c to peg %c", n, frompeg, topeg);
toh(n-1,auxpeg,topeg,frompeg);
}
}

59. Homework #4
1. Define stack as ADT. Describe its primitive operations on Array implementation.
2. Write a Menu program to demonstrate he simulation of stack operations in array
3. implementation.
4. Write recursive algorithm to get nth Fibonacci term. Illustrate it drawing recursion
tree.
5. Explain the algorithm for infix to postfix conversion and evaluation of postfix
expression. Trace the algorithms with suitable example.
6. State TOH problem. Write recursion tree when no. of disks are four.
7. Why recursion is required? Explain with Tower-Of-Hanoi example. How recursive
algorithm makes program effective? Write the merits and demerits of recursion in
programming.
8. Explain in-fix to postfix conversion algorithm. Illustrate it with an example. What
changes should be made for converting infix to prefix?
9. Explain the postfix evaluation algorithm with an example.

60. Thank You !