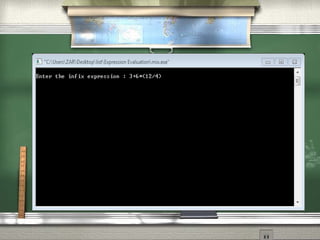
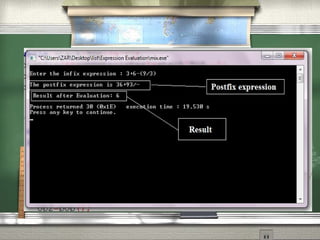
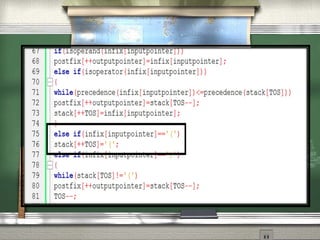
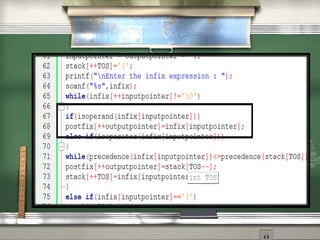
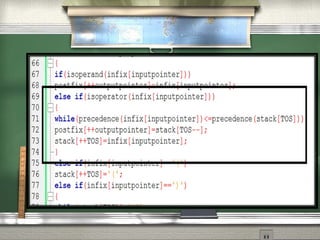
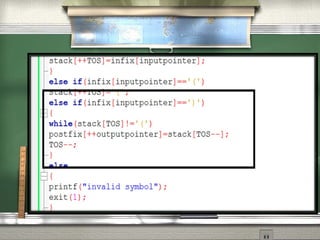
This document discusses different notations for representing mathematical expressions: infix, prefix, and postfix. In infix notation, operators are placed between operands (e.g. A + B). In prefix notation, operators come before operands (e.g. + A B). In postfix notation, operators follow operands (e.g. A B +). It notes that infix notation requires parentheses to determine the order of operations, while prefix and postfix notations do not. The document then provides a step-by-step example of converting an infix expression to postfix notation using a stack.

1. TO OUR
PRESENTATI
ON
WElcOmE…WElcOmE…

2. Submitted By
FASTER
GROUP

3. Group Members

4. Content

5. Prefix, Postfix, Infix
Notation

6. Infix Notation
To add A, B, we write
A+B
To multiply A, B, we write
A*B
The operators ('+' and '*') go in
between the operands ('A' and 'B')
This is "Infix" notation.

7. Prefix Notation
Instead of saying "A plus B", we could
say "add A,B " and write
+ A B
"Multiply A,B" would be written
* A B
This is Prefix notation.

8. Postfix Notation
Another alternative is to put the
operators after the operands as in
A B +
and
A B *
This is Postfix notation.

9. The terms infix, prefix, and postfix
tell us whether the operators go
between, before, or after the
operands.

10. Parentheses
Evaluate 2+3*5.
+ First:
(2+3)*5 = 5*5 = 25
* First:
2+(3*5) = 2+15 = 17
Infix notation requires Parentheses.

11. What about Prefix Notation?
+ 2 * 3 5 =
= + 2 * 3 5
= + 2 15 = 17
* + 2 3 5 =
= * + 2 3 5
= * 5 5 = 25
No parentheses needed!

12. Postfix Notation
2 3 5 * + =
= 2 3 5 * +
= 2 15 + = 17
2 3 + 5 * =
= 2 3 + 5 *
= 5 5 * = 25
No parentheses needed here either!

13. Conclusion:
Infix is the only notation that
requires parentheses.

14. Why all this
At our level, we cannot evaluate an
infix expression, but we can turn an
infix evaluation into a prefix or
postfix expression and then evaluate
them.

15. What we did
We took infix expression and turned
them into postfix expression.

16. Simple way to convert Infix Postfix......

17. Now we want show how we can
convert Infix to Postfix using stack.

18. Now we will see a little bit complex
Example which contain parentheses.

19. Infix to Postfix
( ( A + B ) * ( C - E ) ) / ( F + G ) )
stack: (
output: []

20. Infix to Postfix
( A + B ) * ( C - E ) ) / ( F + G ) )
stack: ( (
output: []

22. Infix to Postfix
A + B ) * ( C - E ) ) / ( F + G ) )
stack: ( ( (
output: []

24. Infix to Postfix
+ B ) * ( C - E ) ) / ( F + G ) )
stack: ( ( (
output: [A]

26. Infix to Postfix
B ) * ( C - E ) ) / ( F + G ) )
stack: ( ( ( +
output: [A]

27. Infix to Postfix
) * ( C - E ) ) / ( F + G ) )
stack: ( ( ( +
output: [A B]

29. Infix to Postfix
* ( C - E ) ) / ( F + G ) )
stack: ( (
output: [A B + ]

30. Infix to Postfix
( C - E ) ) / ( F + G ) )
stack: ( ( *
output: [A B + ]

31. Infix to Postfix
C - E ) ) / ( F + G ) )
stack: ( ( * (
output: [A B + ]

32. Infix to Postfix
- E ) ) / ( F + G ) )
stack: ( ( * (
output: [A B + C ]

33. Infix to Postfix
E ) ) / ( F + G ) )
stack: ( ( * ( -
output: [A B + C ]

34. Infix to Postfix
) ) / ( F + G ) )
stack: ( ( * ( -
output: [A B + C E ]

35. Infix to Postfix
) / ( F + G ) )
stack: ( ( *
output: [A B + C E - ]

36. Infix to Postfix
/ ( F + G ) )
stack: (
output: [A B + C E - * ]

37. Infix to Postfix
( F + G ) )
stack: ( /
output: [A B + C E - * ]

38. Infix to Postfix
F + G ) )
stack: ( / (
output: [A B + C E - * ]

39. Infix to Postfix
+ G ) )
stack: ( / (
output: [A B + C E - * F ]

40. Infix to Postfix
G ) )
stack: ( / ( +
output: [A B + C E - * F ]

41. Infix to Postfix
) )
stack: ( / ( +
output: [A B + C E - * F G ]

42. Infix to Postfix
)
stack: ( /
output: [A B + C E - * F G + ]

43. Infix to Postfix
stack: <empty>
output: [A B + C E - * F G + / ]
Done!!!

46. Thank’s to all
THE END
By Mahadi