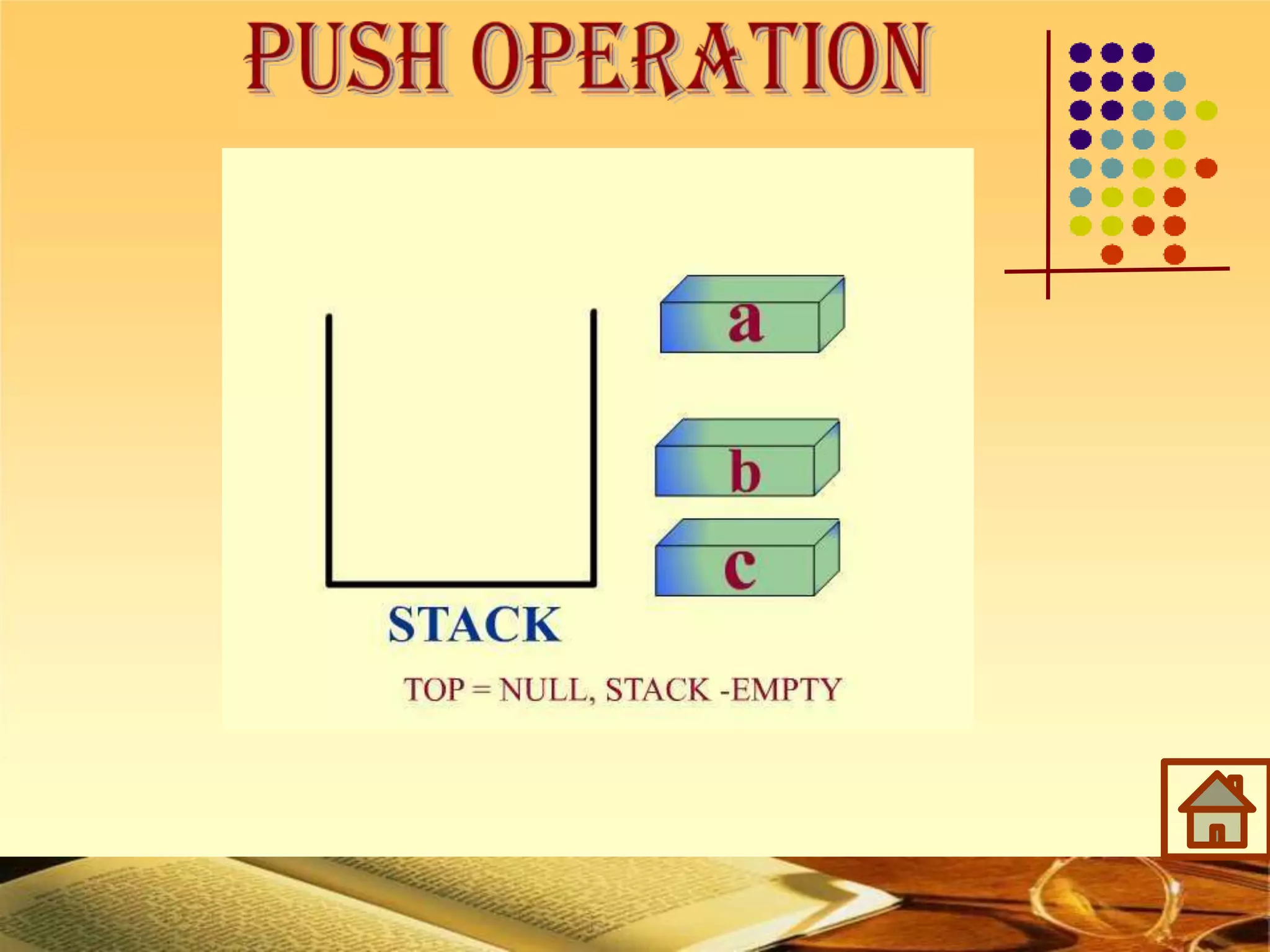
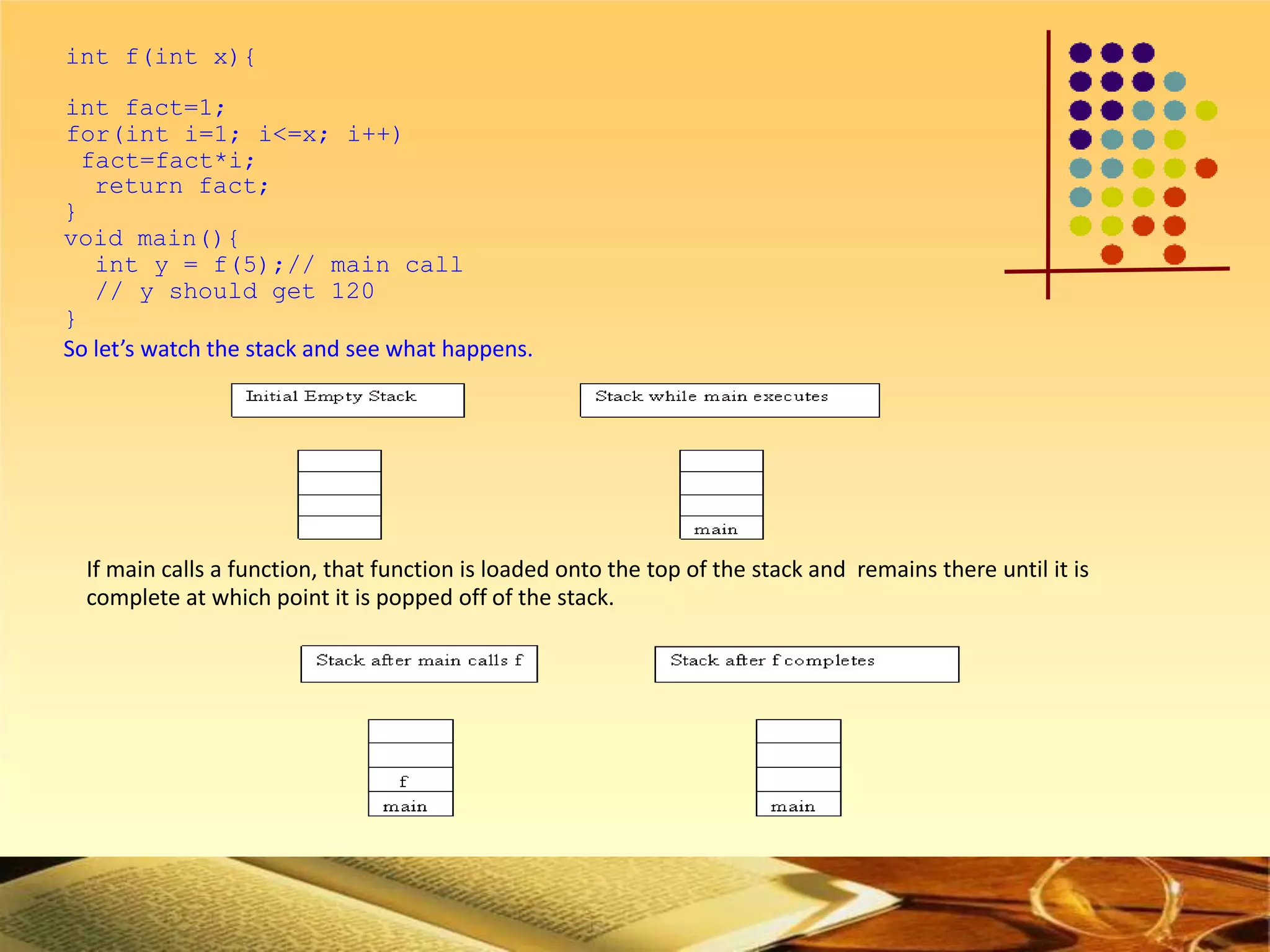
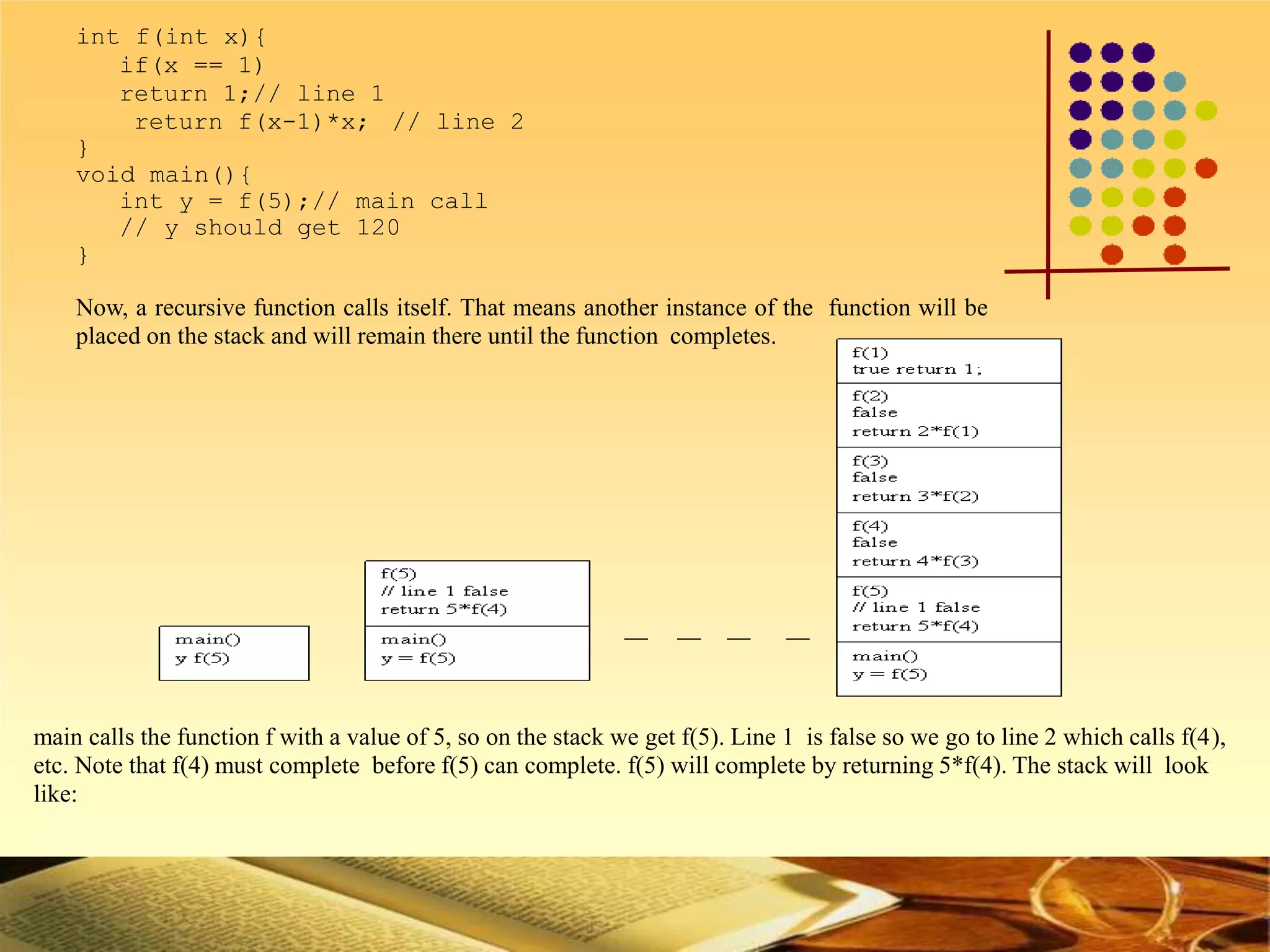
The document discusses stacks and their applications. It defines a stack as a Last In First Out (LIFO) data structure. Key stack operations are described such as push, pop, and peek. An array implementation of a stack is presented and applications like checking balanced brackets, converting infix to postfix notation, and postfix calculators are covered. Example code and diagrams are provided to illustrate stack concepts and operations.

1. A
Data Structure

2.  What is a Stack
 Stack Operations
 LIFO Stack
 Animation Depicting Push Operation
 Animation Depicting Pop Operation
 A r r a y Implementation of Stack
 Applications of s t a c k
Checking f o r balanced br aces
Converting Infix Expression t o Postfix
Postfix c a l c u l a t o r

3. What is a Stack
A stack is a Last In, First Out (LIFO) data structure,
objects inserted last are the first to come out of the stack
Anything added to the stack goes on the “top” of the stack
Anything removed from the stack is taken from the “top” of
the stack
Things are removed in the reverse order from that in which
they were inserted

4. S t a c k Operations
 PUSH
Adds the object to the top of the stack
 POP
Removes the object at the top of the stack
and returns it
 PEEK
Returns the top object of the stack but does
not remove it from the stack
 ISEMPTY
Returns True if Stack is empty

5. A LIFOS t a c k
Top
Bottom
Stack Pointer
Push Pop

8. Array Implementation o f S t a c k
A[1] A[2] …. …. …. A[n]
w y
Stack pointer
J=n
Stack Full
Stack pointer
J=2
Before Push
Stack pointer
J=3
After Push
After many
Push Ops
Push X w y x
Stack Pointer
J=0
Stack Empty
Pop
After many Pop ops
Stack Pointer
J=3
Before Pop
Stack Pointer
J=2
After Pop

9. Implicit and Explicit stack

10. int f(int x){
int fact=1;
for(int i=1; i<=x; i++)
fact=fact*i;
return fact;
}
void main(){
int y = f(5);// main call
// y should get 120
}
So let’s watch the stack and see what happens.
If main calls a function, that function is loaded onto the top of the stack and remains there until it is
complete at which point it is popped off of the stack.

11. int f(int x){
if(x == 1)
return 1;// line 1
return f(x-1)*x; // line 2
}
void main(){
int y = f(5);// main call
// y should get 120
}
Now, a recursive function calls itself. That means another instance of the function will be
placed on the stack and will remain there until the function completes.
main calls the function f with a value of 5, so on the stack we get f(5). Line 1 is false so we go to line 2 which calls f(4),
etc. Note that f(4) must complete before f(5) can complete. f(5) will complete by returning 5*f(4). The stack will look
like:

12. So at this point none of the functions have yet returned! The first to return will be
f(1) which will return 1. Then f(2) will return 2. Then f(3) will return 6. As in:

13. Application of Stack

14. Checking f o r Balanced Bra ces
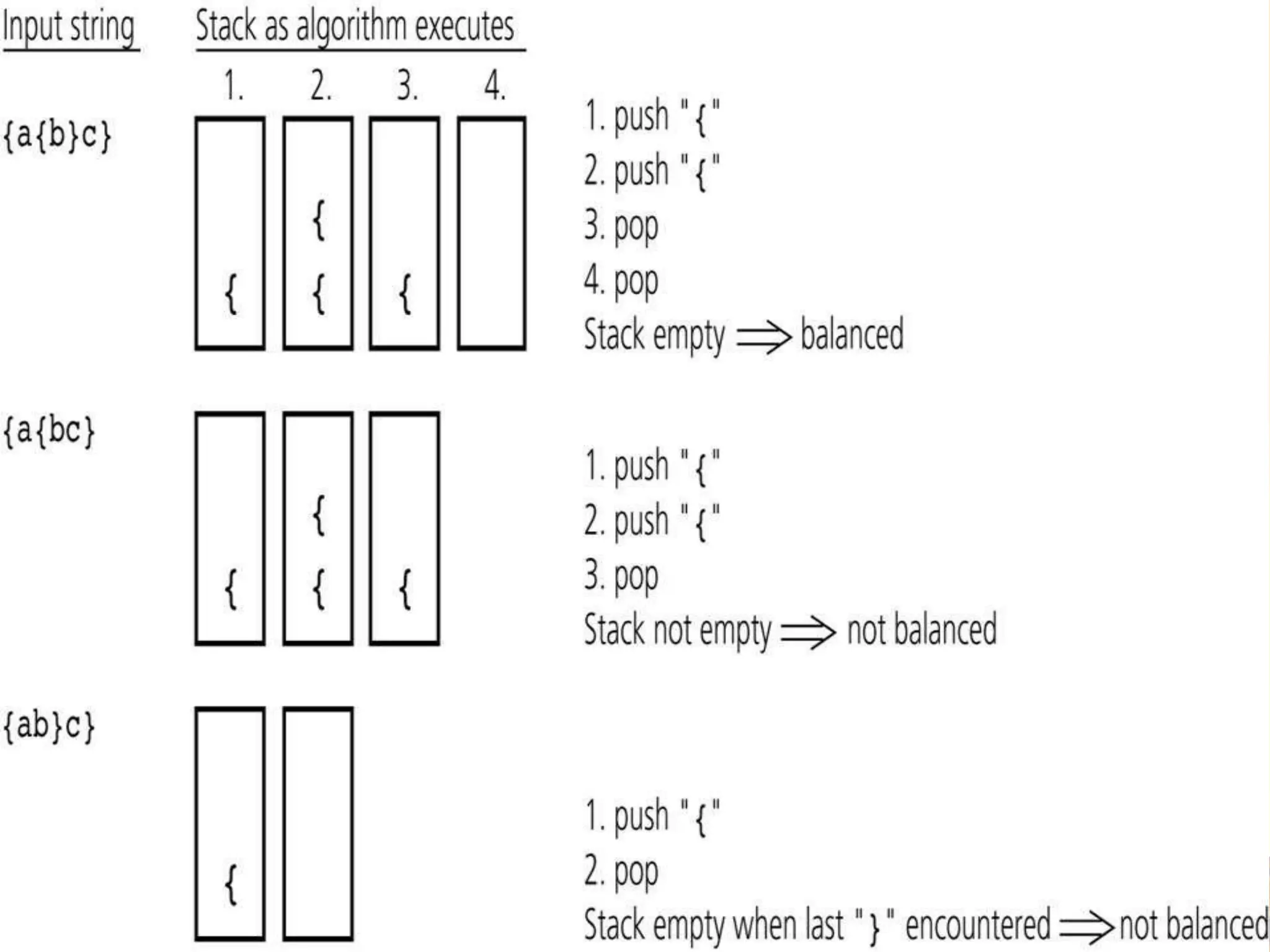
 ([]({()}[()])) is balanced; ([]({()}[())]) is not
 Simple counting is not enough to check balance
 You can do it with a stack: going left to right,
 If you see a (, [, or {, push it on the stack
 If you see a ), ], or }, pop the stack and check
whether you got the corresponding (, [, or {
 When you reach the end, check that the
stack is empty

16. Converting Infix Expressions t o Equivalent
Postfix Expressions
 Infix Expression a+b
 Postfix Expression ab+
 An infix expression can be evaluated by first being
converted into an equivalent postfix expression
 Facts about converting from infix to postfix
 Operands always stay in the same order with respect to
one another
 All parentheses are removed

17. Algorithm : Converting Infix Expression t o
Postfix using s t a c k
Suppose X is an arithmetic expression written in infix notation.
This algorithm finds the equivalent postfix expression Y.
1. Push "(" onto STACK, and add ")" to the end of X.
2. Scan X from left to right and REPEAT Steps 3 to 6 for each element of X UNTIL the
STACK is empty :
3. If an operand is encountered, add it to Y.
4. If a left parenthesis is encountered, push it onto STACK.
5. If an operator is encountered, then :
(a) Repeatedly pop from STACK and add to Y each operator (on the top of STACK) which has
the same precedence as or higher precedence than operator.
(b) Add operator to STACK.
/* End of If structure * /
6. If a right parenthesis is encountered, then :
(a)Repeatedly pop from STACK and add to Y each operator (on the top of STACK)
until a left parenthesis is encountered.
(b) Remove the left parenthesis. [Do not add the left parenthesis to Y].
/* End of If structure * /
/* End of Step 2 loop * /
7. END.

18. A trace of the algorithm that converts the infix expression
a - (b + c * d)/e to postfix form

19. A postfix c a l c u l a t o r
 When an operand is entered, the calculator
 Pushes it onto a stack
 When an operator is entered, the calculator
 Applies it to the top (one or two, depending
on unary or binary operator) operand(s) of
the stack
 Pops the operands from the stack
 Pushes the result of the operation on the
stack

20. The action of a postfix calculator when evaluating the expression 2 * (3 + 4)
Postfix Notation--- 2 3 4 + *