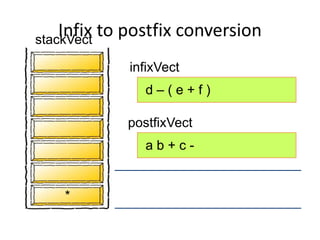
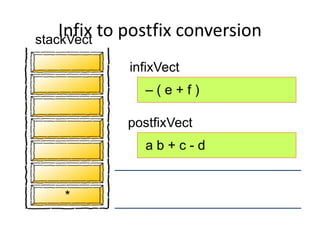
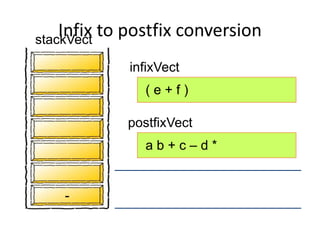
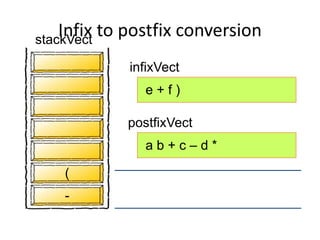
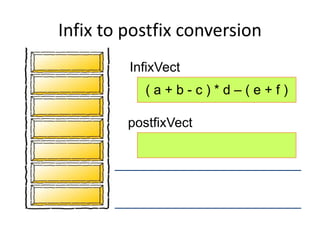
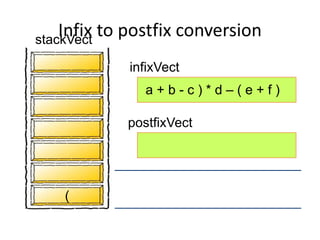
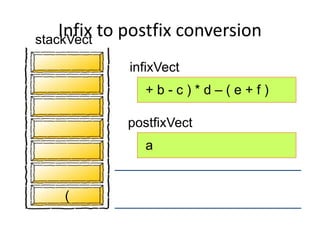
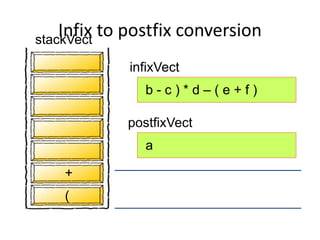
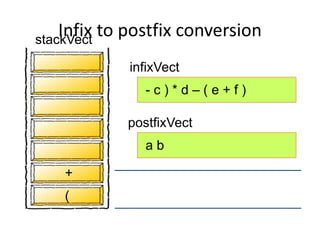
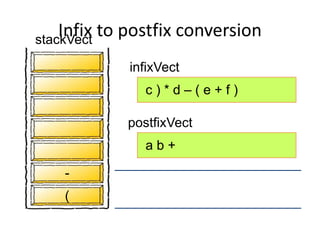
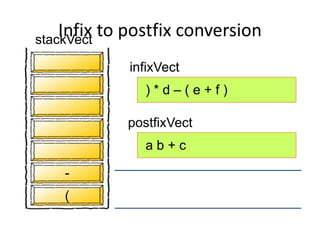
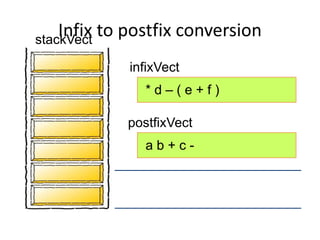
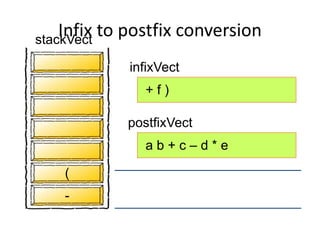
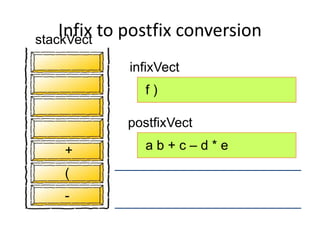
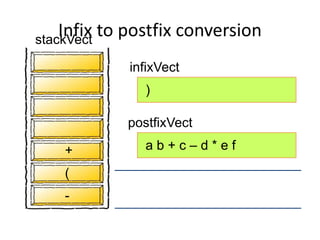
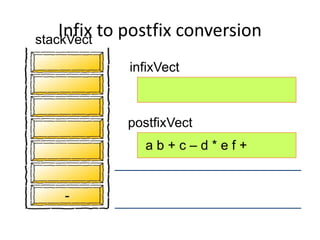
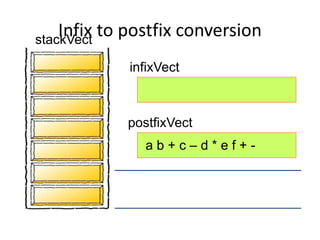
This document discusses applications of stacks, including converting between infix, prefix, and postfix notation. It provides examples of evaluating arithmetic expressions in postfix notation. Key points include: - Prefix notation places the operator before operands, postfix places after, and infix between. - Converting infix to prefix moves operators left and removes parentheses. Converting to postfix moves operators to output list in order of evaluation. 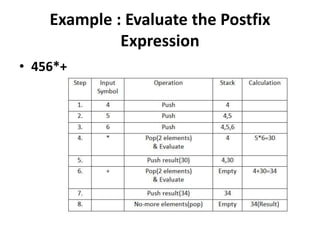- Postfix notation avoids needing parentheses and is evaluated by pushing operands, popping to apply operators, and pushing results back onto the stack.

1. DATA STRUCTURES
Applications of Stacks
Dr. P. Subathra
subathrakishore@yahoo.com
Professor
Dept. of Information Technology
KAMARAJ College of Engineering & Technology
(AUTONOMOUS)
Madurai
Tamil Nadu
India

2. CS8391 – DATA STRUCTURES
ONLINE CLASSES – CLASS NO. 14
25.09.2020
(10:00 AM – 12:00 PM)

3. Applications of Stacks

4. Prefix, Postfix, Infix Notation

5. Infix Notation
• To add A, B, we write
A+B
• To multiply A, B, we write
A*B
• The operators ('+' and '*') go in between the
operands ('A' and 'B')
• This is "Infix" notation.

6. Prefix Notation
• Instead of saying "A plus B", we could say "add
A,B " and write
+ A B
• "Multiply A,B" would be written
* A B
• This is Prefix notation.

7. Postfix Notation
• Another alternative is to put the operators
after the operands as in
A B +
and
A B *
• This is Postfix notation.

8. • The terms infix, prefix, and postfix tell us
whether the operators go between, before, or
after the operands.
Pre A In B Post

9. Parentheses
• Evaluate 2+3*5.
• + First:
(2+3)*5 = 5*5 = 25
• * First:
2+(3*5) = 2+15 = 17
• Infix notation requires Parentheses.

10. What about Prefix Notation?
• + 2 * 3 5 =
= + 2 * 3 5
= + 2 15 = 17
• * + 2 3 5 =
= * + 2 3 5
= * 5 5 = 25
• No parentheses needed!

11. Postfix Notation
• 2 3 5 * + =
= 2 3 5 * +
= 2 15 + = 17
• 2 3 + 5 * =
= 2 3 + 5 *
= 5 5 * = 25
• No parentheses needed here either!

12. Conclusion:
• Infix is the only notation that requires
parentheses in order to change the order in
which the operations are done.

13. CS314 Stacks 13
Mathematical Calculations
• What does 3 + 2 * 4 equal?
2 * 4 + 3? 3 * 2 + 4?
• The precedence of operators affects the order of
operations.
• A mathematical expression cannot simply be evaluated left
to right.
• A challenge when evaluating a program.
• Lexical analysis is the process of interpreting a program.
What about 1 - 2 - 4 ^ 5 * 3 * 6 / 7 ^ 2 ^ 3

14. CONVERSION OF
INFIX
TO
PREFIX AND POSTFIX
EXPRESSIONS

15. Fully Parenthesized Expression
• A FPE has exactly one set of Parentheses
enclosing each operator and its operands.
• Which is fully parenthesized?
( A + B ) * C
( ( A + B) * C )
( ( A + B) * ( C ) )

16. Infix to Prefix Conversion
Move each operator to the left of its operands &
remove the parentheses:
( ( A + B) * ( C + D ) )

17. Infix to Prefix Conversion
Move each operator to the left of its operands &
remove the parentheses:
( + A B) * ( C + D ) )

18. Infix to Prefix Conversion
Move each operator to the left of its operands &
remove the parentheses:
( + AB) * ( C + D ) )

19. Infix to Prefix Conversion
Move each operator to the left of its operands &
remove the parentheses:
( + AB) * +CD ) )

20. Infix to Prefix Conversion
Move each operator to the left of its operands &
remove the parentheses:
( + AB) * + CD ) )

21. Infix to Prefix Conversion
Move each operator to the left of its operands &
remove the parentheses:
* + AB) + CD ) )

22. Infix to Prefix Conversion
Move each operator to the left of its operands &
remove the parentheses:
* + AB) + CD ) )
* + AB)+ CD ) )

23. Infix to Prefix Conversion
Now Remove all the Closing Parenthesis:
* + AB)+ CD ) )
* + AB+ CD

24. Infix to Prefix Conversion
Move each operator to the left of its operands &
remove the parentheses:
* + A B + C D
Order of operands does not change!

25. Infix to Postfix
( ( ( A + B ) * C ) - ( ( D + E ) / F ) )

26. Infix to Postfix
( ( ( A + B ) * C ) - ( ( D + E ) / F ) )
( ( ( AB + * C ) - ( ( D E + / F ) )

27. Infix to Postfix
( ( ( AB + * C ) - ( ( D E + / F ) )
( ( ( AB + C * - ( ( D E + / F ) )
( ( ( AB + C * - ( ( D E + F / )
( ( ( AB +C * - ( ( D E + F / )

28. Infix to Postfix
( ( ( AB +C * - ( ( D E + F / )
( ( ( AB +C * - ( ( D E + F / )
( ( ( AB +C * ( ( D E + F / -
( ( ( AB +C * ( ( D E + F / -

29. Infix to Postfix
( ( ( AB +C * ( ( D E + F / -
( ( ( AB +C * ( ( D E + F / -
Remove all open parenthesis
AB +C * D E + F / -
Postfix Expression: AB +C * D E + F / -
• Operand order does not change!
• Operators are in order of evaluation

30. Infix to Postfix
• Initialize a Stack for operators, output list
• Split the input into a list of tokens.
• for each token (left to right):
if it is operand: append to output
if it is '(': push onto Stack
if it is ')': pop & append till '('
if it in '+-*/':
while peek has precedence ≥ it:
pop & append
push onto Stack
pop and append the rest of the Stack.

31. Operators Precedence & Associativity Table
Operator Precedence

32. InfixVect
postfixVect
( a + b - c ) * d – ( e + f )
Infix to postfix conversion

33. infixVect
postfixVect
a + b - c ) * d – ( e + f )
(
stackVect
Infix to postfix conversion

34. infixVect
postfixVect
+ b - c ) * d – ( e + f )
(
a
Infix to postfix conversionstackVect

35. infixVect
postfixVect
b - c ) * d – ( e + f )
(
a
+
Infix to postfix conversionstackVect

36. infixVect
postfixVect
- c ) * d – ( e + f )
(
a b
+
Infix to postfix conversionstackVect

37. infixVect
postfixVect
c ) * d – ( e + f )
(
a b +
-
Infix to postfix conversionstackVect

38. infixVect
postfixVect
) * d – ( e + f )
(
a b + c
-
Infix to postfix conversionstackVect

39. infixVect
postfixVect
* d – ( e + f )
a b + c -
Infix to postfix conversionstackVect

40. infixVect
postfixVect
d – ( e + f )
a b + c -
*
Infix to postfix conversionstackVect

41. infixVect
postfixVect
– ( e + f )
a b + c - d
*
Infix to postfix conversionstackVect

42. infixVect
postfixVect
( e + f )
a b + c – d *
-
Infix to postfix conversionstackVect

43. infixVect
postfixVect
e + f )
a b + c – d *
-
(
Infix to postfix conversionstackVect

44. infixVect
postfixVect
+ f )
a b + c – d * e
-
(
Infix to postfix conversionstackVect

45. infixVect
postfixVect
f )
a b + c – d * e
-
(
+
Infix to postfix conversionstackVect

46. infixVect
postfixVect
)
a b + c – d * e f
-
(
+
Infix to postfix conversionstackVect

47. infixVect
postfixVect
a b + c – d * e f +
-
Infix to postfix conversionstackVect

48. infixVect
postfixVect
a b + c – d * e f + -
Infix to postfix conversionstackVect

49. Infix to Postfix Expression
https://www.youtube.com/watch?v=OVFwgYrM
Shw

50. Infix to Prefix Expression
• https://www.youtube.com/watch?v=sJ0VhIbv
Ctc

51. EVALUATION OF POSTFIX EXPRESSION
SIMPLE POSTFIX EXPRESSION EVALUATION

52. Evaluation Rule of a Postfix
Expression States
• While reading the expression from left to
right, push the element in the stack if it is an
operand.
• Pop the two operands from the stack, if the
element is an operator and then evaluate it.
• Push back the result of the evaluation.
• Repeat it till the end of the expression.
• Finally the result is in the Stack

53. Example : Evaluate the Postfix
Expression
• 456*+

54. Evaluation of Postfix Expression
https://www.youtube.com/watch?v=uh7fD8WiT
28