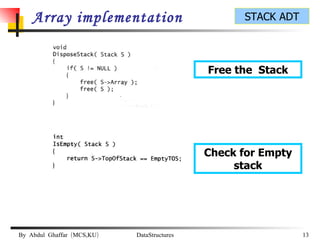
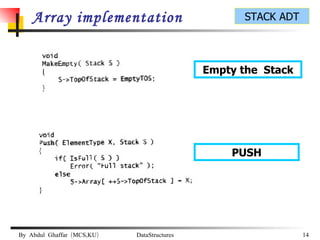
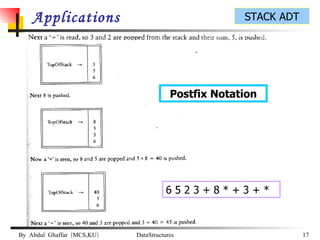
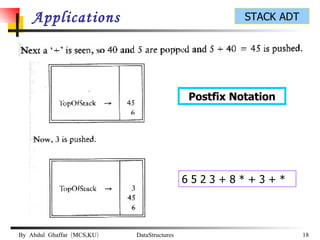
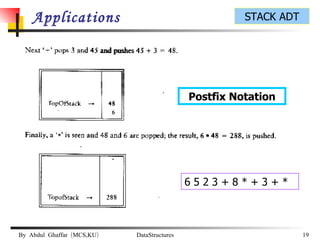
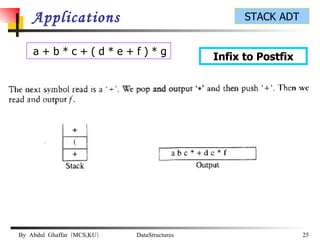
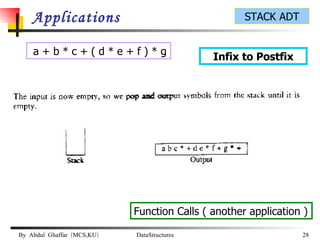
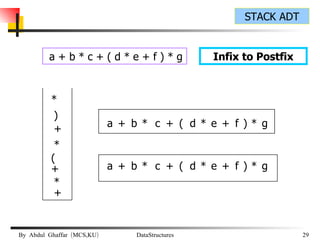
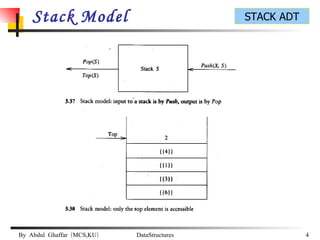
The document discusses stacks and their implementation as linked lists and arrays. It defines a stack as a last-in, first-out data structure where insertion and deletion can only occur at one end, called the top. The key stack operations are push, which inserts at the top, pop, which removes from the top, and top, which retrieves the top element. Stacks have applications in postfix notation and converting infix to postfix expressions.

1. S T A C K Based on Chapter 3 Of Reference Book #1

2. Reference Books Data Structures and Algorithm Analysis in C By Mark Allen Weiss Published by Addison Wesley Data Structures (Schaum’s Outline Series) By Seymour Lipschutz Published by Mc Graw Hill

3. A STACK Model Definitions A STACK is a list with the restriction that insertion and deletion can be performed in only one position.for that reason it is called LIFO (last in first out ) structure. The end where insertion and deletion can be performed is called the end of the list or top. Set of operations PUSH , i nserts a new element at the end or top . POP , deletes or remove most recently inserted element from top. TOP, retrieves most recently inserted element from top. isEmpty , returns the status of emptiness of the stack. A pop operation on top on an empty stack is considered as an error. A push on a full stack cause a overflow condition.

4. Stack Model

5. Implementation As Linked List PUSH = insertion at front of the list. POP = retrieving and deletion at the front of the list TOP = retrieving the value of the front node

6. Linked List implementation Declarations

7. Linked List implementation Empty Test Create Stack

8. Linked List implementation PUSH TOP

9. Linked List implementation POP

10. Implementation As Array Define an Array ‘ Stack ’ of sufficient capacity to store stack elements. Uses a variable i.e TopOfStack to remember the position of TOP. TopOfStack = -1 for an empty stack. PUSH: Set TopOfStack = TopOfStack +1 Set Stack[TopOfStack] = X POP: Return Stack[TopOfStack] Set TopOfStack = TopOfStack –1

11. Array implementation Declarations

12. Array implementation Create Stack

13. Array implementation Free the Stack Check for Empty stack

14. Array implementation Empty the Stack PUSH

15. Array implementation TOP POP TOP and POP

16. Applications Postfix Notation

17. Applications Postfix Notation 6 5 2 3 + 8 * + 3 + *

18. Applications Postfix Notation 6 5 2 3 + 8 * + 3 + *

19. Applications Postfix Notation 6 5 2 3 + 8 * + 3 + *

20. Applications Infix to Postfix a + b * c + ( d * e + f ) * g

21. Applications Infix to Postfix a + b * c + ( d * e + f ) * g

22. Applications Infix to Postfix a + b * c + ( d * e + f ) * g

23. Applications Infix to Postfix a + b * c + ( d * e + f ) * g

24. Applications Infix to Postfix a + b * c + ( d * e + f ) * g

25. Applications Infix to Postfix a + b * c + ( d * e + f ) * g

26. Applications Infix to Postfix a + b * c + ( d * e + f ) * g

27. Applications Infix to Postfix a + b * c + ( d * e + f ) * g

28. Applications Infix to Postfix a + b * c + ( d * e + f ) * g Function Calls ( another application )

29. a + b * c + ( d * e + f ) * g Infix to Postfix a + b * c + ( d * e + f ) * g a + b * c + ( d * e + f ) * g + * + ( * + ) *