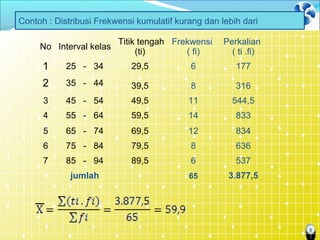
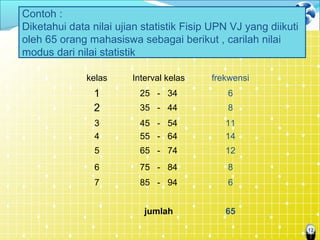
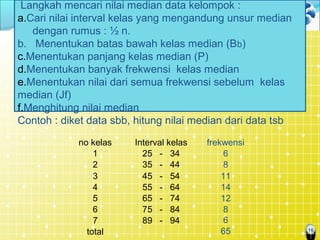
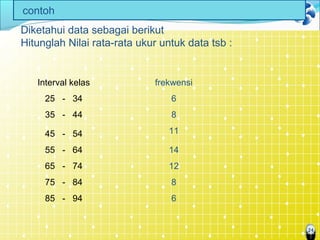
Dokumen tersebut membahas mengenai ukuran pemusatan data atau statistik deskriptif, yang merupakan nilai data yang mewakili seluruh data. Beberapa ukuran pemusatan data yang dijelaskan adalah rata-rata hitung, modus, dan median untuk data tunggal maupun kelompok beserta contoh perhitungannya. Juga dijelaskan mengenai rata-rata ukur untuk menghitung rata-rata kenaikan data.

1. 1
Ukuran Pemusatan Data
(Statistik Deskriptif)
A. Pengertian
Ukuran Pemusatan Data adalah suatu nilai data dari
serangkaian data yang dapat mewakili data tersebut.
Beberapa macam ukuran pemusatan data :
1. Rata –rata Hitung
adalah jumlah dari serangkaian data dibagi dengan
jumlah data . _
Simbul rata- rata hitung untuk sampel ( X ) .
Simbul rata- rata hitung untuk populasi (µ).
Perhitungan rata –rata hitung dibagi kedalam tiga jenis
data :

2. 2
a) Rata – rata hitung ( mean ) Data Tunggal
caranya adalah menjumlah semua data yang ada ,
kemudian dibagi dengan banyaknya data .
= meanx
n = jumlah data
Atau
= Nilai tiap data

3. 3
b) Rata – rata hitung ( mean ) Data Berbobot
= meanx
ni = jumlah tiap-tiap kelompok data
= Jumlah rata-rata
Jika ada kelompok sudah data yang sudah diketahui nilai rata-ratanya, maka untuk
Mencari semua rata-rata dihitung dengan rata-rata saja.

4. 4
* Buat tabel penolong sbb:
No Wilayah
Jum fotografi
(ni)
Rata-rata
penghasilan
(xi)
Jumlah
penghasilan
(xi .ni)
1 Jakarta 2 10 juta 20 juta
2 Bandung 4 15 juta 60 juta
3 Yogyakarta 4 20 juta 80 juta
4 Surabaya 5 25 juta 125 juta
15 285 juta
Contoh
Pengusaha fotografi Makmur mempunyai 15 buah kios
cabang yang tersebar di 4 (empat) daerah .
di Jakarta ada 2 buah kios cabang dg penghasilan Rp. 10
Juta /tahun , Bandung ada 4 buah kios cabang dg peng
-hasilan Rp. 15 Juta /tahun, Yogyakarta ada 4 buah kios
cabang dg penghasilan Rp. 20 Juta /tahun, Surabaya ada
5 buah kios cabang dg penghasilan Rp. 25 Juta /tahun .
Berapa rata-rata penghasilan fotografi setiap tahun.

5. 5
* Rata-rata penghasilan fotografi setiap tahun

6. 6
C) Rata – rata Hitung (mean) Data Kelompok
Untuk menghitung mean data kelompok adalah nilai
tengah dari setiap kelas dikalikan dengan frekwensi dari
setiap kelas, kemudian hasil perkalian tersebut
dijumlahkan untuk dibagi dengan jumlah frekwensi.

7. 7
kelas Interval kelas frekwensi
1 25 - 34 6
2 35 - 44 8
3 45 - 54 11
4 55 - 64 14
5 65 - 74 12
6 75 - 84 8
7 85 - 94 6
jumlah 65
contoh :
Diketahui nilai statistik mahasiswa FISIP UPN Veteran
Jakarta yang diikuti oleh 65 0rang mahasiswa sbb :
Berapa nilai rata–rata hitung nilai statistik mahasiwa ?

8. 8
No Interval kelas
Titik tengah
(ti)
Frekwensi
( fi)
Perkalian
( ti .fi)
1 25 - 34 29,5 6 177
2 35 - 44 39,5 8 316
3 45 - 54 49,5 11 544,5
4 55 - 64 59,5 14 833
5 65 - 74 69,5 12 834
6 75 - 84 79,5 8 636
7 85 - 94 89,5 6 537
jumlah 65 3.877,5
Contoh : Distribusi Frekwensi kumulatif kurang dan lebih dari

9. 9
2.Modus
Modus adalah nilai dari beberapa data yang mempunyai
frekwensi tertinggi baik data tunggal maupun data berdistribusi
atau nilai yang paling sering muncul dalam suatu kelompok data
1). Modus Data Tunggal
Menghitung modus ini dengan cara mencari nilai
yang paling sering muncul diantara sebaran data.
Contoh :
Nilai UTS 10 orang mahasiswa : 50 , 60 , 70 , 75 , 70
, 70 , 80 , 75 , 70 , 75 .
Maka modus nilai UTS adalah 70 karena muncul 4
( empat )kali.

10. 10
2.Modus Data kelompok
Mo = Bb + P ( F1 )
F1 + F2
Mo = Modus
Bb = Batas bawah kelas yang mengandung nilai modus
P = Panjang kelas
F1 = Selisih antara nilai frekwensi dikelas modus ( f) dengan
frekwensi sebelum kelas modus ( f sb)
F2 = Selisih antara nilai frekwensi dikelas modus ( f) dengan
frekwensi sesudah kelas modus ( f sd)

11. 11
2.Langkah mencari modus Data kelompok :
a) Cari nilai frekwensi yang terbanyak untuk dijadikan kelas
Modus
b) Cari batas bawah kelas modus (Bb) => Batas bawah
interval kelas dikurangi 0,5.
c) Hitung panjang kelas modus (P)
d) Carilah : F1 = f – Fsb.
e) Carilah : F2 = f – Fsd.
f) Menghitung modus

12. 12
kelas Interval kelas frekwensi
1 25 - 34 6
2 35 - 44 8
3 45 - 54 11
4 55 - 64 14
5 65 - 74 12
6 75 - 84 8
7 85 - 94 6
jumlah 65
Contoh :
Diketahui data nilai ujian statistik Fisip UPN VJ yang diikuti
oleh 65 orang mahasiswa sebagai berikut , carilah nilai
modus dari nilai statistik

13. 13
Langkah :
a. Mencari nilai frekwensi yang terbanyak yaitu 14, nilai
Modus terletak diinterval kelas ke 4.
b. Bb = 55 - 0,5 = 54,5
c. Panjang kelas modus .
P = 55 sampai 64 = 9
d. F1 = f - Fsb. = 14 - 11 = 3
e. F2 = f - Fsd. = 14 – 12 = 2
f. Nilai modus
Mo = Bb + P
= 54,5 + 9 ( 3 ) = 59,9
3+2

14. 14
3. Median
Median (Me) adalah nilai tengah dari suatu gugusan, data
yang telah disusun dari data terkecil sampai data terbesar
atau sebaliknya dari data terbesar sampai data terkecil.
1) Median data tunggal
Me = ½ ( 1+ n ) n = jumlah data
Contoh :
Diketahui data sbb : 80, 70, 30, 50, 40, 75, 75, 75, 65.
Carilah median data tsb.
a. Urutkan data dari terkecil sampai terbesar :
30, 40, 50, 65, 70, 75, 75, 75,80
b. Posisi median  Me = ½ ( 9 +1 ) = 5
Posisi Me pada data ke 5
jadi nilai, Me = 70

15. 15
Lanjutan.
2) Median data kelompok
Me = Bb + P ( ½ .n – Jf )
f
Me = Median
Bb = Batas bawah kelas yang mengandung nilai median .
P = Panjang kelas
n = Jumlah data
f = Banyak frekwensi kelas median.
Jf = jumlah dari semua frekwensi kumulatif sebelum
kelas median .

16. 16
no kelas Interval kelas frekwensi
1 25 - 34 6
2 35 - 44 8
3 45 - 54 11
4 55 - 64 14
5 65 - 74 12
6 75 - 84 8
7 89 - 94 6
total 65
Langkah mencari nilai median data kelompok :
a.Cari nilai interval kelas yang mengandung unsur median
dengan rumus : ½ n.
b. Menentukan batas bawah kelas median (Bb)
c.Menentukan panjang kelas median (P)
d.Menentukan banyak frekwensi kelas median
e.Menentukan nilai dari semua frekwensi sebelum kelas
median (Jf)
f.Menghitung nilai median
Contoh : diket data sbb, hitung nilai median dari data tsb

17. 17
lanjutan
a. Nilai interval yang mengandung unsur median
½. n = ½. 65 = 32,5
Selanjutnya menentukan kelas median dengan menjumlah
kan nilai frekwensi dari kelas awal sampai dengan kelas yg
menunjukkan hasil penjumlahan mencapai nilai 32,5 atau
lebih .
6 + 8 +11 + 14 = 39 jadi median terletak dikelas ke- 4
b. Menentukan batas bawah kelas median (Bb).
Bb = 55 - 0,5 = 54,5
c. Menentukan panjang kelas median. P = 55 sampai 64 =9
d. Menentukan jumlah frekwensi dikelas median (f) =14
e. Carilah jumlah semua frekwensi kumulatif dibawah kelas
median. Jf = 6 + 8 + 11 = 25 .

18. 18
lanjutan
f. Menghitung nilai median
Me = Bb + P ( ½ .n - Jf )
f
= 54,5 + 9 ( ½ . 65 - 25 )
14
= 59,4

19. 19
4. Rata- rata Ukur
adalah rangkaian data dari akar pangkat n dari hasil perkali
an nilai datanya . Gunanya adalah untuk mencari rata-rata
kenaikan dalam bentuk persentase, perbandingan setiap
data berurutan yang hampir tetap, menghitung rata-rata
terhadap persentase atau ratio perubahan suatu gejala
pada data tertentu .
1) Rata -rata ukur data tunggal
a. Bila data relatif kecil .
RU = Rata –rata Ukur . N = Banyak data. Xn = data .
Contoh : diketahui data X1= 2 , X2=4 , X3 =8
Maka
n
RU = √ X1. X2. X3…………….Xn
3 3
RU = √2 x 4 x 8 = √64 = 4

20. 20
lanjutan
b. Bila data relatif besar .
Log RU = ∑ Log Xi
n
RU = anti log RU -100
Xi = presentase perubahan setiap data
n = jumlah data

21. 21
minggu Penghasilan (Rp) Persentase (%)
I 750.000,- -
II 650.000,- 650.000/750.000x100%= 86,66
III 700.000,- 700.000/650.000x100%= 107,70
IV 500.000,- 500.000/700.000x100%= 71,44
V 680.000,- 680.000/500.000x100%= 136
VI 1.200.000,- 1.200.000/680.000x100%= 176,5
Langkah
Diketahui penghasilan setiap PKL di Jakarta mingguan sbb
I . Rp. 750.000,- III . Rp. 700.000,- V. Rp. 680.000,-
II . Rp. 650.000,- IV. Rp. 500.000,- VI. Rp.1.200.000,
Berapa rata-rata ukur penghasilan setiap mingguan
a. Menentukan nilai persentase perubahan (Xn)

22. 22
no Xn (%) Log.X
1 86,66 1,9375
2 107,70 2,0322
3 71,44 1,8539
4 136 2,1335
5 176,5 2,2467
jumlah ∑ Log X = 10,2038
lanjutan
b. Nilai persentase (%) diubah menjadi nilai Log
X1 = 86,66 X2 = 107,70 X3 = 71,44
X4= 136 X5= 176,5
c. Mencari setiap nilai Xn menjadi nilai log .

23. 23
lanjutan
d. Rata –rata ukur (RU).
Log RU = ∑ Log X = 10,2038 = 2,0407
n 5
RU = anti log 2,0407 -100 = 9,8
= 109,8 - 100 = 9,8 %
Pendapatan PKL mengalami kenaikan 9,8% per
minggu.
2) Rata –rata ukur data kelompok .
Log RU = ∑ f.Log ti
∑f
RU = anti log RU

24. 24
Interval kelas frekwensi
25 - 34 6
35 - 44 8
45 - 54 11
55 - 64 14
65 - 74 12
75 - 84 8
85 - 94 6
contoh
Diketahui data sebagai berikut
Hitunglah Nilai rata-rata ukur untuk data tsb :

25. 25
a. Buat tabel penolong dengan menambah kolom titik
tengah ( ti) , log ti dan f.log ti
No
Interval
kelas
Frekwensi
( fi)
Titik
tengah
(ti)
Log .ti
Perkalian
( fi .log ti)
1 25 - 34 6 29,5 1,4698 8,819
2 35 - 44 8 39,5 1,5966 12,77
3 45 - 54 11 49,5 1,6946 18,64
4 55 - 64 14 59,5 1,7745 24,84
5 65 - 74 12 69,5 1,842 22,1
6 75 - 84 8 79,5 1,9004 15,2
7 85 - 94 6 89,5 1,9518 11,71
jumlah 114,1
lanjutan

26. 26
lanjutan
b. Nilai rata-rata ukur
 Log RU = ∑ f . Log ti
 ∑ f
= 114,1 = 1,7554
65
Ru = anti log 1,7554
= 56,94

27. 27
Terima
Kasih