Relasi merupakan hubungan antara dua himpunan. Dokumen menjelaskan definisi relasi, contoh relasi, sifat-sifat relasi seperti refleksif, simetris, transitif, dan operasi-operasi pada relasi seperti invers dan komposisi relasi. Dokumen juga membahas relasi kesetaraan, kelas kesetaraan, matriks relasi, dan klosur relasi. [/ringkasan]

1. RELASI
Matematika Diskrit

2. Definisi
• Relasi (binair) R dari himpunan X ke himpunan Y
adalah sebuah subhimpunan dari hasil kali
Cartesius X x Y.
• Notasi :
Jika (x,y) ∈ R maka :
x R y  x relasi dengan y
• Daerah asal (domain) dari R :
{x ∈ X | (x,y) ∈ R untuk beberapa y ∈ Y}
• Daerah hasil (range) dari R :
{y ∈ Y | (x,y) ∈ R untuk beberapa x ∈ X}
Matematika Diskrit
2

3. Contoh 1
• X = {Nani, Rianti, Dudi,
Ivan, Candra}
• Y = { Teknik Informatika,
Matematika, Manajemen
Informatika, Teknik Sipil}
• R = {(Nani, Teknik
Informatika), (Rianti,
Matematika), (Dudi,
Manajemen Informatika),
(Ivan, Manajemen
Informatika), (Candra,
Teknik Sipil)}
Matematika Diskrit
X
Nani
Rianti
Dudi
Ivan
Candra
Y
T.
Informatika
Matematika
Manaj.
Informatika
Manaj.
Informatika
T. Sipil
3

4. Pasangan terurut dalam relasi R
Matematika Diskrit
4

5. Contoh 2
• X = {2,3,4}
• Y = { 3,4,5,6,7}
• R = {(2,4), (2,6), (3,3), (3,6), (4,4)}
X
Y
2
4
2
6
3
3
3
6
4
4
Matematika Diskrit
• Domain dari R = {2,3,4}
• Range dari R = { 3,4, 6}
5

6. Digraf
• Cara informatif untuk menggambarkan
sebuah relasi pada sebuah himpunan
• Memiliki :
 vertex (ujung)
 directed edge
(rusuk berarah)
Matematika Diskrit
6

7. Sifat-sifat Relasi
•
•
•
•
•
•
Refleksif
Anti refleksif
Simetris
Antisimetris
Transitif
Non transitif
Matematika Diskrit
7

8. Refleksif
• Relasi R pada himpunan X disebut refleksif
jika (x,x) ∈ R untuk setiap x ∈ X
• Digraf dari refleksif mempunyai sebuah
loop pada setiap ujungnya.
• Contoh :
X = {1,2,3,4}
R = {(1,1),(1,2),(1,3),
(1,4),(2,2),(2,3),
(2,4),(3,3),(3,4),
(4,4)}
Matematika Diskrit
8

9. Tidak Refleksif
• Salah satu atau lebih vertex
tidak mempunyai loop
• Contoh :
X = {1,2,3,4}
R = {(1,1),(2,3),(3,2),(4,4)}
Matematika Diskrit
9

10. Simetris
• Relasi R pada himpunan X disebut
simetris jika untuk semua x, y ∈ X,
jika (x,y) ∈ R maka (y,x) ∈ R
• Digraf dari relasi simetris
mempunyai sifat bahwa terdapat
rusuk berarah dari v ke w, maka
juga terdapat rusuk berarah dari
w ke v
Matematika Diskrit
10

11. Simetris (Cont.)
• Contoh :
X = {1,2,3,4}
R = {(1,1),(2,3),(3,2),(4,4)}
(2,3) di R dan (3,2)
di R
Matematika Diskrit
11

12. Antisimetris (Tidak Simetris)
• Relasi R pada himpunan X disebut
antisimetris jika untuk semua x, y ∈ X,
jika (x,y) ∈ R dan x ≠ y, maka (y,x) ∉ R
• Digraf dari relasi antisimetris mempunyai
sifat bahwa diantara sembarang 2 ujung
terdapat rusuk 2 arah
Matematika Diskrit
12

13. Antisimetris (Cont.)
• Contoh :
X = {1,2,3,4}
R = {(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),
(2,4),(3,3),(3,4),(4,4)}
(2,3) ∈ R tetapi
(3,2) ∉ R
Matematika Diskrit
13

14. Transitif
• Relasi R pada himpunan X disebut
transitif jika untuk semua x,y,z ∈X,
jika (x,y) dan (y,z) ∈ R, maka (x,z) ∈ R
• Digraf dari relasi transitif mempunyai
sifat bahwa apabila terdapat rusuk
berarah dari x ke y dan dari y ke z, maka
terdapat rusuk berarah dari x ke z.
Matematika Diskrit
14

15. Transitif (Cont.)
Pasangan berbentuk
(x,y)
(y,z)
(x,z)
Pasangan berbentuk
(x,y)
(y,z)
(x,z)
(1,1)
(1,1)
(1,1)
(2,2)
(2,2)
(2,2)
(1,1)
(1,2)
(1,2)
(2,2)
(2,3)
(2,3)
(1,1)
(1,3)
(1,3)
(2,2)
(2,4)
(2,4)
(1,1)
(1,4)
(1,4)
(2,3)
(3,3)
(2,3)
(1,2)
(2,2)
(1,2)
(2,3)
(3,4)
(2,4)
(1,2)
(2,3)
(1,3)
(2,4)
(4,4)
(2,4)
(1,2)
(2,4)
(1,4)
(3,3)
(3,3)
(3,3)
(1,3)
(3,3)
(1,3)
(3,3)
(3,4)
(3,4)
(1,3)
(3,4)
(1,4)
(3,4)
(4,4)
(3,4)
(1,4)
(4,4)
(1,4)
(4,4)
(4,4)
(4,4)
Matematika Diskrit
15

16. Transitif (Cont.)
• Penentuan sebuah relasi R transitif :
1. jika (x,y) dan (y,z) ∈ R, maka (x,z) ∈ R
2. x = y dan (x,z) = (y,z) di R
• Contoh :




R1 = {(1,1),(1,2),(2,1),(2,2),(3,4),(4,1),(4,4)}  tidak transitif
R2 = {(1,1),(1,2),(2,1)}  tidak transitif
R3 = {(1,1),(1,2),(1,4),(2,1),(2,2),(3,3),(4,1),(4,4)}  tidak transitif
R4 = {(2,1),(3,1),(3,2),(4,1),(4,2),(4,3)}  transitif
Matematika Diskrit
16

17. Urutan Parsial (Partial Orders)
• Relasi R pada himpunan X disebut
urutan parsial jika R
refleksif,
antisimetris dan
transitif
• Ketiga persyaratan tersebut harus
dipenuhi
Matematika Diskrit
17

18. Invers
• Misalkan R adalah relasi dari X ke Y maka
invers dari R adalah relasi dari Y ke X
• Notasi : R-1
• Invers didefinisikan :
R-1 = {(y,x) | (x,y) ∈ R}
• Digambarkan relasi ini sebagai “terbagi
oleh”
• Contoh :
R = {(2,4), (2,6), (3,3), (3,6), (4,4)}
R-1 = {(4,2), (6,2), (3,3), (6,3), (4,4)}
Matematika Diskrit
18

19. Komposisi (Composite)
• Misalkan R1 adalah relasi dari X ke Y dan R2
adalah relasi dari Y ke Z, maka komposisi dari
R1 dan R2 adalah relasi dari X ke Z
• Notasi : R2 ° R1
• Komposisi didefinisikan :
R2 ° R1 = {(x,z) | (x,y) ∈ R1 dan (y,z)∈ R2 untuk beberapa y ∈ Y}
• Contoh :
R1 = {(1,2),(1,6),(2,4),(3,4),(3,6),(3,8)}
R2 = {(2,u),(4,s),(4,t),(6,t),(8,u)}
R2 ° R1 = {(1,u),(1,t),(2,s),(2,t),(3,s),(3,t),(3,u)}
Matematika Diskrit
19

20. Relasi Keekuivalenan
• Teorema 1 :
 Misalkan S adalah partisi dari himpunan
X. Definisikan xRy untuk mengartikan
bahwa untuk beberapa himpunan S di S,
baik x maupun y berada di S, maka R
refleksif, simetris dan transitif
• Sebuah relasi yang refleksif, simetris
dan transitif pada himpunan X
disebut relasi keekuivalenan pada X
(equivalence relation on X)
Matematika Diskrit
20

21. Relasi Keekuivalenan (Cont.)
• Contoh :
S = {{1,3,5},{2,6},{4}}
X = {1,2,3,4,5,6}
R = {(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),(2,2),
(2,6),(6,2),(6,6),(4,4)}
• Digraf relasi dari R harus :
 Refleksif :
terdapat sebuah loop pada setiap ujungnya
 Simetris :
untuk setiap rusuk berarah dari v ke w juga
terdapat
rusuk berarah dari w ke v
 Transitif :
jika terdapat sebuah rusuk berarah dari x ke y dan
rusuk berarah dari y ke z maka terdapat rusuk
berarah
dari x ke z
Matematika Diskrit
21

22. Relasi Keekuivalenan (Cont.)
Matematika Diskrit
22

23. Teorema 2
• Misalkan R sebuah relasi keekuivalenan pada
himpunan X. Untuk setiap a ∈ X, misalkan :
{a} = {x ∈ X | xRa}
Sehingga :
S = {[a] | a ∈ X}
adalah partisi dari X
• Misalkan R adalah relasi keekuivalenan pada
himpunan X. Himpunan-himpunan [a] yang
didefinisikan pada Teorema 2 disebut kelas
keekuivalenan dari X yang diberikan oleh
relasi R
Matematika Diskrit
23

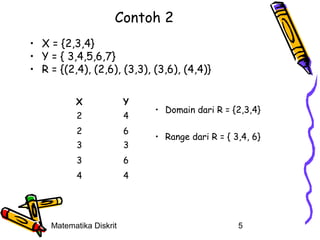
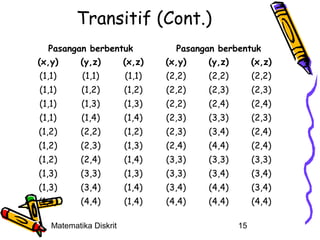
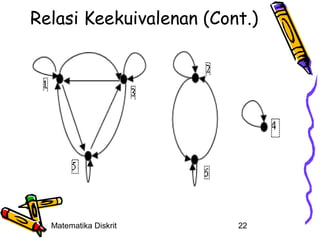
24. Contoh
• S = {{1,3,5},{2,6},{4}}
X = {1,2,3,4,5,6}
R = {(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),
(5,3),(5,5),(2,2),(2,6),(6,2),(6,6),(4,4)}
Kelas keekuivalenan [1] yang mengandung 1
terdiri dari semua y sehingga (1,y) ∈ R. Oleh
karena itu :
[1] = {1,3,5}
Kelas ekuivalenan yang tersisa didapatkan
dengan cara yang sama :
[3] = [5] = {1,3,5}
[2] = [6] = {2,6}
[4] = {4}
Matematika Diskrit
24

25. Teorema 3
• Misalkan R adalah relasi keekuivalenan
pada himpunan terhingga X. Jika setiap
kelas keeukuivalenan mempunyai r unsur,
maka terdapat |X| / r kelas keekuivalenan
X1
X2
…….
(r unsur) (r unsur)
Xk
(r unsur)
|X| = r k
|X| = |X1| + |X2| + … + |Xk|
=r+r+…+r=rk
Matematika Diskrit
25

26. Matriks Relasi
• Dikenal dengan adjacency matrix
• Contoh :
R = {(1,b),(1,d),(2,c),(3,c),(3,b),(4,a)}
X = {1,2,3,4}
Y = {a,b,c,d}
a b c d
1 0
2 0

3 0

4 1
Matematika Diskrit
1
0
1
0
0
1
1
0
1
0

0

0
26

27. Klosur Relasi
• Klosur relasi terjadi jika :
Relasi tidak refleksif menjadi refleksif
 Klosur refleksif (Reflexive Closure)
Relasi tidak simetris menjadi simetris
 Klosur simetris (Symmetric Closure)
Relasi tidak transitif menjadi transitif
Klosur transitif (Transitive Closure)
Matematika Diskrit
27

28. Klosur refleksif (Reflexive Closure)
•
Klosur refleksif dari R adalah :
R ∪ ∆ , dimana ∆ = {(a,a)|a ∈ A}
•
Contoh :
1. A = {1, 2, 3}
R = {(1,1), (1,3), (2,3), (3,2)}  tidak refleksif
Supaya bersifat refleksif maka ∆ = {(1,1), (2,2), (3,3)}
Sehingga klosur refleksif dari R adalah :
R ∪ ∆ = {(1,1), (1,3), (2,3), (3,2)} ∪ (1,1), (2,2), (3,3)}
= {(1,1), (1,3), (2,2), (2,3), (3,2), (3,3)}
2. R = {(a,b)|a ≠ b} pada himpunan bilangan bulat
Maka klosur refleksif dari R adalah :
R ∪ ∆ = {(a,b)|a ≠ b} ∪ {(a,a)|a ∈ Z}
= {(a,b)|a ∈ Z}
Matematika Diskrit
28

29. Klosur Simetris (Symmetric Closure)
• Klosur simetris dari R adalah :
R ∪ R-1 , dimana R-1 = {(a,b)| (b,a) a ∈ R}
• Contoh :
1. A = {1, 2, 3}
R = {(1,3), (1,2), (2,1), (3,2), (3,3)}
Supaya bersifat simetris maka R-1 = {(3,1), (2,1), (1,2), (2,3), (3,3)}
Sehingga klosur simetris adalah :
R ∪ R-1 = {(1,3), (1,2), (2,1), (3,2), (3,3)} ∪ {(3,1), (2,1), (1,2), (2,3), (3,3)}
= {(1,3), (3,1), (1,2), (2,1), (3,2), (2,3), (3,3)}
2. R = {(a,b)|a habis membagi b} pada himpunan bilangan bulat
Maka klosur simteris dari R adalah :
R ∪ R-1 = {(a,b)|a habis membagi b} ∪ {(b,a)|b habis membagi a}
= {(a,b)|a habis membagi b atau b habis membagi a}
Matematika Diskrit
29

30. Klosur Transitif (Transitive Closure)
• Klosur transitif dari R adalah :
∞
R =  R = R ∪ R ∪ R
*
n
2
3
n
n =1
atau
M R * = M R ∨ M R[ 2 ] ∨ M R[ 3 ] ∨  ∨ M R *
Matematika Diskrit
30

31. Contoh
A = {1, 2, 3}
R = {(1,1), (1,3), (2,2), (3,1), (3,2)}
Matriks yang merepresentasikan relasi R adalah :
1 0 1
M R = 0 1 0 


1 1 0


Klosur transitif dari R adalah :
Karena
Maka
M R * = M R ∨ M R[ 2 ]
M R[ 2 ]
M R * = M R ∨ M R [ 2 ] ∨ M R[ 3 ]
∨ MR
[ 3]
1 1 1 
1 1 1 
= M R . M R = 0 1 0 dan M R[ 3 ] = M R[ 2 ] . M R = 0 1 0




1 1 1 
1 1 1 




Sehingga klosur transitif R* : {(1,1), (1,2), (1,3), (2,2), (3,1), (3,2), (3,3)}
Matematika Diskrit
31

32. Latihan
Jika diketahui X = {1,2,3,4}
Tentukan relasi berikut memiliki sifat transitif atau
tidak :
1. R1 = {(1,1),(2,1),(2,2),(2,3),(3,1),(4,2)}
2.
R2 = {(1,2),(1,3),(2,2),(2,3),(3,2),(4,4)}
3.
R3 = {(1,1),(1,3),(2,2),(2,4),(3,1),(3,2)}
4.
R4 = {(1,3),(2,1),(2,3),(3,2),(3,3)}
5.
R5 = {(1,2),(1,4),(2,2),(2,3),(3,4),(3,2),(4,1)}
Matematika Diskrit
32

33. Latihan
Jika A = {0, 1, 2, 3}
R = {(0,1), (1,1), (1,2),(2,0), (2,2)}
Tentukan :
6. Klosur transitif
7. Klosur simetris
Jika A = {1, 2, 3,4}
R = {(2,1), (2,3), (3,1), (3,4), (4,1), (4,3)}
Tentukan :
8. Klosur refleksif
9. Klosur simetris
10. Klosur transitif
Matematika Diskrit
33