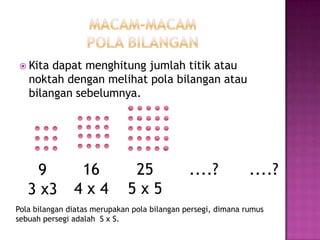
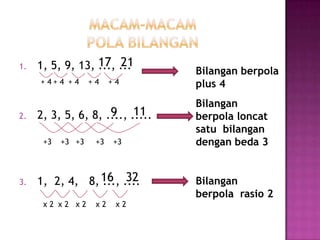
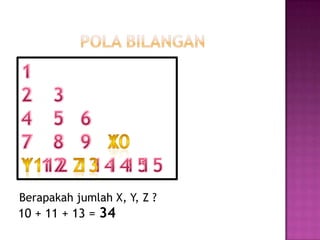
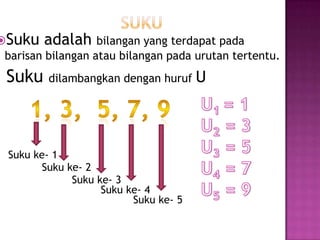
Dokumen tersebut membahas tentang pola bilangan dan barisan aritmatika. Secara ringkas, pola bilangan adalah susunan bilangan yang memiliki aturan tertentu, sementara barisan aritmatika adalah kumpulan bilangan yang memiliki selisih yang tetap antara bilangan satu dengan yang lainnya.

1. CREATED BY:
FARIDA ARIANI, S.Pd

2. +1 +2 +3 +4
 PolaBilangan adalah kumpulan bilangan yang
jika di jajarkan akan membentuk suatu pola
atau aturan rumus tertentu.

3.  Polabilangan tidak selalu berupa angka,
tetapi juga dapat berupa kumpulan noktah
atau titik.
Pola persegi Pola Pola
panjang segi tiga persegi

4.  Kita dapat menghitung jumlah titik atau
noktah dengan melihat pola bilangan atau
bilangan sebelumnya.
9 16 25 ....? ....?
3 x3 4x4 5x5
Pola bilangan diatas merupakan pola bilangan persegi, dimana rumus
sebuah persegi adalah S x S.

5. 1. 1, 5, 9, 13, 17 ...
..., 21 Bilangan berpola
+ 4+ 4 + 4 +4 +4 plus 4
Bilangan
2. 9 11
2, 3, 5, 6, 8, ...., ..... berpola loncat
satu bilangan
+3 +3 +3 +3 +3 dengan beda 3
3. 1, 2, 4, 8, 16 ....
..., 32 Bilangan
berpola rasio 2
x2 x2 x2 x2 x2

6. 1. Pola bilangan Naik yaitu pola bilangan
yang nilainya semakin besar.
Contoh: 2,4,6,8, dst.
2. Pola bilangan Turun yaitu pola bilangan
yang nilainya semakin kecil.
Contoh: 32, 16, 8, 4, 2, 1, dst.

7. Berapakah jumlah X, Y, Z ?
10 + 11 + 13 = 34

8. Suku adalah bilangan yang terdapat pada
barisan bilangan atau bilangan pada urutan tertentu.
Suku dilambangkan dengan huruf U
Suku ke- 1
Suku ke- 2
Suku ke- 3
Suku ke- 4
Suku ke- 5

9.  BARISAN ARITMATIKA adalah kelompok bilangan
yang memiliki beda (selisih) yang tetap.
Contoh barisan aritmatika:
1, 5, 9, 13, ..., ...
 Unsur-unsur Barisan Aritmatika:
a = bilangan di urutan pertama
b = beda/ selisih dari dua bilangan yang
berurutan
Un = suku/bilangan pada urutan ke-n

10. Ciri dari BARISAN ARITMATIKA adalah:
1. Memiliki beda yang tetap
1, 5, 9, 13
2. Beda/selisih berupa
penjumlahan/pengurangan
Penjumlahan: 2, 4, 6, 8, 10, dst
+2 +2 +2 +2
Pengurangan: 33, 30, 27, 24, 21 dst.
-3 -3 -3 -3

11. 1, 5, 9, 13, ..., ...
 Suku ke- n pada BARISAN ARITMATIKA
dapat ditulis dengan rumus:
Maka suku ke-5 dari barisan aritmatika diatas
adalah:

12.  Menentukan suku ke-n yang sudah diketahui
rumusnya.
contoh soal:
1. Tentukan suku ke 12 dari Un= n2 + 3
jawab:

13. contoh soal:
jumlah bangku di barisan pertama gedung
bioskop adalah 8. Pada barisan selanjutnya
selalu bertambah 4 bangku. Tentukan :
a. Jumlah bangku pada baris ke 5!

14. DERET ARITMATIKA adalah jumlah dari
barisan bilangan/jumlah dari seluruh
suku yang ada.
DERET BILANGAN dilambangkan dengan
huruf S.
contoh: 1,3,5,7,9
maka S5 = U1 + U2 + U3 + U4 + U5
S5 = 1 + 3 + 5 + 7 + 9
S5 = 25

15. contoh soal:
jumlah baris tempat duduk digedung bioskop
4 baris. bangku di barisan pertama gedung
bioskop adalah 8. Pada barisan selanjutnya
selalu bertambah 4 bangku. Tentukan :
a. Jumlah bangku di gedung
Jawab: n
(2a (n 1)b
2
4
(2.8 (4 1)4
2
2 (16 (3)4
2 (16 12 ) 2 28
56

16. contoh soal:
jumlah baris tempat duduk digedung bioskop
8 baris. bangku di barisan pertama gedung
bioskop adalah 8. Pada barisan selanjutnya
selalu bertambah 5 bangku. Tentukan :
a. Jumlah bangku di gedung
Jawab:

17. contoh soal:
hitunglah deret aritmatika dari 1+4+7+10 +....+
298!
Jawab:
1. Did you know total suku dari baris bilangan
diatas?
2. Suku keberapa 298 itu??
Un 298 3n 2 298
a (n 1).b 298 3n 298 2
3n 300
1 (n 1) x3 298 n 300 : 3
n 100
1 (3n 3) 298

18. contoh soal:
hitunglah deret aritmatika dari 1+4+7+10 +....+
298!
Jawab:
Ternyata jumlah suku diatas ada 100. maka deret
bilangannya: