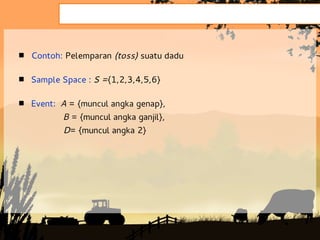
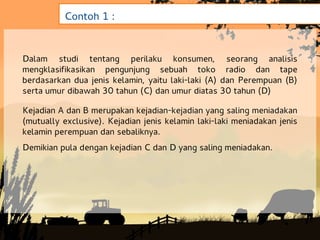
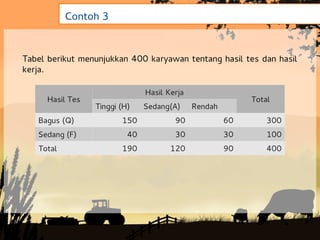
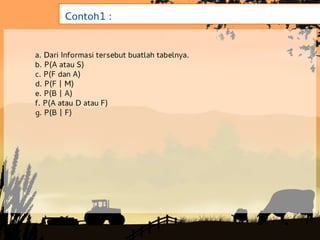
Dokumen tersebut membahas tentang konsep dasar probabilitas dan beberapa pendekatan untuk menghitung nilai probabilitas. Probabilitas digunakan untuk mengukur kemungkinan terjadinya suatu peristiwa dan nilainya berkisar antara 0 hingga 1. Ada tiga pendekatan untuk menghitung probabilitas yaitu pendekatan klasik, frekuensi relatif, dan subyektif.

1. PROBAILITAS
Mempelajari probabilitas sangat berguna untuk pengambilan
keputusan yang tepat, karena kehidupan di dunia tidak ada
kepastian, sehingga perlu untuk mengetahui berapa besar
probabilitas suatu peristiwa akan terjadi. Probabilitas
dinyatakan dalam angka pecahan antara 0 sampai 1 atau dalam
persentase. Beberapa istilah penting dalam probabilitas adalah
(a) percobaan, (b) hasil, dan (c) peristiwa.

2. Review : Beberapa Konsep
PERCOBAAN : (1) Proses yang menghasilkan data mentah.
(2) Pengamatan terhadap beberapa aktivitas atau
proses yang memungkinkan timbulnya paling
sedikit dua peristiwa tanpa memperhatikan
peristiwa mana yang akan terjadi.
2 Sifat : (1) Setiap jenis percobaan mempunyai beberapa
kemungkinan hasil atau peristiwa (event) yang akan terjadi (possible
outcomes).
(2) Hasil setiap percobaan secara pasti sulit
ditentukan.

3. Review : Beberapa Konsep
Percobaan adalah peristiwa yang melahirkan suatu peristiwa=
kejadian = event.
Percobaan melempar koin akan menghasilkan peristiwa muncul
gambar atau angka.
Kegiatan jual-beli saham akan melahirkan peristiwa membeli
atau menjual saham.
Perubahan harga akan melahirkan peristiwa Inflasi atau Deflasi
Pertandingan sepak bola akan melahirkan peristiwa menang, seri
atau kalah.

4.  Contoh: Pelemparan (toss) suatu dadu
 Sample Space : S ={1,2,3,4,5,6}
 Event: A = {muncul angka genap},
B = {muncul angka ganjil},
D= {muncul angka 2}

5. Review : Beberapa Konsep
Dalam kebanyakan hal, hasil suatu percobaan akan tergantung kepada
keboleh-jadian dan oleh karena itu tidak dapat diramalkan dengan
pasti.
Sebuah mata uang yang dilantunkan beberapa kali, kita tidak akan
pernah dapat memastikan bahwa suatu lantunan tertentu akan
menghasilkan “muka”.
Akan tetapi kita tahu seluruh kemungkinan yang dapat terjadi untuk
setiap lantunan.

6. Review : Beberapa Konsep
Ruang Sample :
Ruang Contoh = sample space adalah Himpunan semua hasil yang
mungkin dari suatu percobaan (total possible outcomes) yang
dilambangkan dengan S
Titik Sample :
Titik Contoh (sample point) adalah elemen-elemen (anggota-anggota
atau unsur-unsur) dari ruang sample

7. Review : Beberapa Konsep
Kejadian :
Peristiwa = event, merupakan himpunan bagian dari ruang sample
atau bagian dari hasil percobaan yang diinginkan.
Jenis Kejadian :
Kejadian sederhana = elementer adalah kejadian yang hanya
mempunyai satu titik sample.
Kejadian Majemuk adalah kejadian mempunyai titik sample
lebih dari satu.

8. Review : Beberapa Konsep
Kejadian elementer = kejadian sederhana adalah himpunan bagian
dari kejaidan majemuk.
Kejadian elementer atau kejadian majemuk adalah himpunan bagian
dari ruang sample.
Gabungan dari beberapa kejadian elementer membentuk kejadian
majemuk dan gabungan dari semua kejadia elementer membentuk
ruang sample.

9. PROBABILITAS ?
Kata probabilitas== peluang == kemungkinan
Probabilitas merupakan peluang bahwa sesuatu akan terjad,. atau
Suatu nilai yang digunakan untuk mengukur tingkat terjadinya suatu
kejadian yang acak (random).
Probabilitas biasanya dinyatakan dengan bilangan desimal atau
bilangan pecahan.
Nilai probabilitas berkisar antara 0 dan 1. Semakin dekat nilai
probabilitas ke nilai 0 maka semakin kecil kemungkinan suatu
kejadian akan terjadi dan sebaliknya.

10. PENDEKATAN PERHITUNGAN PROBABILITAS
Ada 3 (tiga) pendekatan konsep untuk mendefinisikan probabilitas dan
menentukan nilai-nilai probabilitas, yaitu :
(1). Pendekatan Klasik
(2). Pendekatan Frekuensi Relatif, dan
(3). Pendekatan Subyektif

11. PENDEKATAN KLASIK
Pendekatan klasik didasarkan pada banyaknya kemungkinan-
kemungkinan yang dapat terjadi pada suatu kejadian.
Jika a banyaknya kemungkinan yang dapat terjadi pada kejadian A dan
b banyaknya kemungkinan yang tidak terjadi pada kejadian A, serta
masing-masing kejadian mempunyai kesempatan yang sama dan saling
asing, maka probabilitas bahwa kejadian A akan terjadi adalah :
a
P(A) =
a+b

12. Contoh PENDEKATAN KLASIK :
contoh1 : Suatu perusahaan memiliki 30 karyawan pria (B) dan 15
karyawan wanita. Masing-masing karyawan mempunyai kartu
presensi. Berapakah probabilitas yang diambil secara acak milik
karyawan wanita ?
contoh2 : Pelamar pekerjaan terdiri dari 10 pria dan 15 wanita, jika
yang diterima hanya satu, maka berapakah probabilitas bahwa ia
seorang pria ?
contoh3 : Jika kita percaya bahwa kejadia A dua kali lebih besar bila
dibandingkan dengan kejadian B, Berapakah probabilitas kejadian A ?

13. PENDEKATAN FREKUENSI RELATIF :
Dengan pendekatan ini, nilai probabilitas ditentukan atas dasar
proporsi dari kemungkinan yang dapat terjadi dalam suatu observasi
atau percobaan.
Tidak ada asumsi awal tentang kesamaan kesempatan, karena
penentuan probabilitas didasarkan pada hasil obeservasi atau
pengumpulan data.
Disebut juga emprirical approach

14. Contoh : PENDEKATAN FREKUENSI RELATIF :
Contoh1 : misalkan berdasarkan pengalaman empirik, pada
pengambilan data sebanyak N, terdapat a kejadian yang bersifat A,
maka probabilitas akan terjadi A untuk data N adalah :
a
P(A) =
N

15. Contoh : PENDEKATAN FREKUENSI RELATIF :
Contoh2 : sebelum diadakan training untuk 100 karyawan, diedarkan
angket terlebih dahulu. Dari angket tersebut didapat informasi bahwa
terdapat 5 karyawan akan sakit gigi jika berada pada cuaca dingin. Jika
training tetap diadakan pada daerah dengan cuaca dingin, maka
probabilitas seorang akan mengalami sakit gigi adalah . . .
5
P(A) =
100

16. Contoh : PENDEKATAN FREKUENSI RELATIF :
Contoh3 :suatu catatan memperlihatkan bahwa dalam 180 hari dari
200 hari, sebuah supermarket menjual 225 – 300 kaleng susu.
berapakah probabilitas penjualan kaleng susu sebanyak 225 – 300 ?
180
P(A) =
200

17. PENDEKATAN SUBJEKTIF
Pendekatan subjektif dalam penentuan probabilitas adalah tepat atau
cocok jika hanya ada satu kemungkinan kejadian terjadi dalam satu
kejadian.
Dengan pendekatan ini, nilai probabilitas suatu kejadian ditentukan
berdasarkan tingkat kepercayaan yang bersifat individual dengan
berlandaskan pada semua petunjuk yang dimilikinya.
Karena nilai probabilitas merupakan keputusan pribadi atau individual
pendekatan ini sering disebut sebagai personal approach.

18. PENYAJIAN PROBABILITAS
Simbol P digunakan untuk melambangkan nilai probabilitas suatu
kejadian. Dengan demikian P(A) berarti probabilitas bahwa kejaian A
akan terjadi dalam observasi atau percobaan tunggal.
Nilai probabilitas terkecil adalah 0 yang berarti tidak mungkin terjadi,
dan nilai tertinggi adalah 1 yang menyatakan suatu kejadian pasti
terjadi.

19. PENYAJIAN PROBABILITAS
Jika dalam suatu observasi, kemungkinan kejadian ada 2 yaitu terjadi
dan tidak terjadi, dengan demikian jumlah probabilitas terjadi dan
tidak terjadi sama dengan 1

20. Kejadian
Meniadakan dan tidak meniadakan

21. Pengertian :
2 kejadian atau lebih disebut saling meniadakan == mutually
exclusive jika kejadian-kejadian tersebut tidak dapat terjadi
bersamaan.
Satu kejadian tertentu akan menghalangi atau meniadakan satu atau
lebih kejadian yang lain.
2 kejadian atau lebih disebut tidak saling meniadakan == non
mutually exclusive jika kejadian-kejadian tersebut dapat terjadi
bersamaan.

22. Contoh 1 :
Dalam studi tentang perilaku konsumen, seorang analisis
mengklasifikasikan pengunjung sebuah toko radio dan tape
berdasarkan dua jenis kelamin, yaitu laki-laki (A) dan Perempuan (B)
serta umur dibawah 30 tahun (C) dan umur diatas 30 tahun (D)
Kejadian A dan B merupakan kejadian-kejadian yang saling meniadakan
(mutually exclusive). Kejadian jenis kelamin laki-laki meniadakan jenis
kelamin perempuan dan sebaliknya.
Demikian pula dengan kejadian C dan D yang saling meniadakan.

23. Contoh 1
Akan tetapi kejadian A dan dan kejadian C merupakan kejadian yang
tidak saling meniadakan (non mutually exclusive) artinya kejadian-
kejadian tersebut dapat terjadi bersama-sama.
Misalnya : ada pengunjung laki-laki dan berumur kurang dari 30
tahun.

24. Contoh 2
Seorang analisis sebuah bank mengambil data secara acak (random)
dari sepuluh berkas yang diajukan oleh enam perusahaan komputer
(A) dan empat perusahaan tekstil (B).
Empat dari perusahaan komputer dan dua dari perusahaan tekstil
telah go-public (C).
Dua kejadian A dan B saling meniadakan, kejadian perusahaan
komputer meniadakan perusahaan tekstil dan sebaliknya. Sedangkan
kejadian B dan C disebut kejadian yang tidak saling meniadakan, sebab
dapat terjadi berkas yang diambil adalah perusahaan tekstil dan go-
public.

25. Contoh 3
Tabel berikut menunjukkan 400 karyawan tentang hasil tes dan hasil
kerja.
Hasil Kerja
Hasil Tes Total
Tinggi (H) Sedang(A) Rendah
Bagus (Q) 150 90 60 300
Sedang (F) 40 30 30 100
Total 190 120 90 400

26. Contoh 3
Probabilitas bahwa pengambilan secara random adalah seorang
karyawan yang memiliki hasil tes bagus adalah :
300
P(Q) = 0.75
400
Probabilitas kejadian F dan H
40
P(H∩F) = 0.10
400

27. Contoh 3
Kejadian hasil tes bagus dan hasil test sedang merupakan kejadian
yang mutually exclusive ==kejadian yang saling meniadakan. Oleh
karena itu kejadian seorang karyawan yang memiliki hasil tes bagus
dan hasil test sedang adalah :
P(Q∩F) = 0

28. Hukum
PENJUMLAHAN

29. Aturan Probabilitas
Hukum penjumlahan digunakan jika kita akan menghitung probabilitas
suatu kejadian tertentu atau yang lain (atau keduanya) yang terjadi
dalam suatu percobaan (observasi) tunggal.
Secara simbolis kita dapat menyatakan probabilitas kejadian A atau
kejadian B yang muncul atau yang terjadi dengan lambang P(A atau B)
yang dalam teori himpunan disebut probabilitas gabungan yang
dilambangkan dengan P(A  B)

30. Aturan Penjumlahan
Hukum penjumlahan tergantung dari apakah dua kejadian saling
meniadakan atau tidak saling meniadakan,
Addition Rule = utk dua events A dan B yg terpisah/ disjoint (no
common outcomes = mutually exclusive) :
P (A or B) = P(A) + P (B)
Contoh: Lempar suatu dadu: S = {1,2,3,4,5,6};
mis A = {2}, B = {1,3,5}; P(A or B) = P(A) + P(B) = 1/6 + 1/2 =
2/3

31. Aturan Penjumlahan
Hukum penjumlahan untuk kejadian yang tidak saling meniadakan :
1. Dua kejadian
P(A atau B) = P(A) + P(B) – P(A dan B) atau
P(A  B ) = P(A) + P(B) – P(A  B)
2. Tiga kejadian
P(A atau B atau C) = P(A) + P(B) + P(C) – P(A dan B)
- P( A dan C) - P(B dan C) + P(A dan B dan C)
P(A  B ) = P(A) + P(B) + P(C) – P(A  B) - P(A  C) -
P(B  C) + P(A B C)

32. Contoh1 :
Dengan menggunaakan tabel diatas, tentukan probabilitas kejadian
seorang karyawan yang memiliki hasil kerja tinggi atau sedang.
Jawab :
Karena kejadian karyawan yang mempunyai hasil kerja tinggi dan hasil
kerja sedang merupakan kejadian yang saling meniadakan, maka :
kejadian karyawan yang mempunyai kerja tinggi atau sedang adalah :
P(H atau A) = P(H) + P(A) = (190 + 120) / 400 = 0.775

33. Contoh2 :
Berdasarkan tabel di bawah, berapakah probabilitas bahwa
pengambilan data perusahaan secara random akaan terpilih
perusahaan yang memiliki laba per tahun :
a. Diantara 10 juta s.d 19 juta
b. kurang dari 20 juta
c. Salah satu dari kelompok ektrim (kurang dari 10 juta atau lebih dari
40 juta).

34. Contoh2 :
Jumlah
Kategori Batasan Laba per tahun
Perusahaan
A < 10 juta 60
B 10 juta s.d 19.999 juta 100
C 20 juta s.d 20,999 juta 160
D 30 juta s.d 39.999 juta 140
E 40 juta s.d 40,999 juta 40
Total 500
Jawab : a. P(B) = 100/500
b. P(A atau B) = 60/500 + 100/500
c. P(A atau E) = 60/500 + 40/500

35. Contoh3 :
Dari seratus perusahaan, 40 diantaranya menggunakan personal
komputer (P) dan 30 perusahaan menggunakan mini komputer (M).
Dari 70 perusahaan di atas, 20 diantaranya menggunakan personal
komputer dan mini komputer.
a. Buatlah diagram venn untuk menggambarkan kondisi di atas.
b. Berapakah probabilitas pada pengambilan secara random akan
terjadi perusahaan yang menggunakan personal komputer atau mini
komputer ?
c. Berapakah probabilitas pada pengambilan secara random akan
terjadi perusahaan hanya menggunakan salah satu dari personal
komputer atau mini komputer ?

36. Jawab Contoh3 :
b. P(P atau M) = P(P) + P(M) – P(P dan M)
P(P atau M) = 0.40 + 0.30 – 0.20 = 0.50
c. P(P atau M, tidak keduanya) = P(P atau M) – P(P dan M)
P(P atau M, tidak keduanya) = 0.5 - 0.20 = 0.30

37. Contoh4 :
Sebuah perusahaan memproduksi 3 jenis sabun (A, B, dan C)
mengadakan penelitian pada 200 pengunjung toko swalayan. Dari
penelitian tersebut diperoleh data sbb :
52 orang menggunaann sabun jenis A, 53 menggunakan sabun jenis B,
40 menggunakan sabun C.
25 orang menggunakan sabun jenis A dan B, 12 orang jenis sabun A
dan C, 13 orang menggunakan jenis B dan C, 5 orang menggunakan
jenis sabun A, B dan C.
a. Berapa probabilitas orang yang tidak menggunakan sabun dari
perusahaan tersebut ?
b. Berapa probabilitas pengunjung yang hanya menggunakan satu jenis
sabun dari perusahaan tersebut ​

38. Jawab Contoh4 :
P(A BC) = P(A) + P(B) + P(C) – P(AC) – P(AB) – P(BC) +
P(A  BC
a. P(tidak menggunakan A, B atau C) = 1 - P(A BC)
b. P(pengunjung hanya menggunakan satu jenis produk tsb) =
P(A, B, atau C saja) = P(A BC) - P(AC) – P(AB) – P(BC) -
2P(A  BC

39. Kejadian Dependent
Independent dan Bersyarat

40. Konsep :
Berdasarkan pengaruh atau tidaknya suatu kejadian terhadap kejadian
lain, kejadian-kejadian dibedakan menjadi 2, yakni kejadian yang
dependent dan kejadian yang independent.
Dua kejadian dikatakan independent apabila terjadi atau tidaknya
suatu kejadian tidak berpengaruh kepada probabilitas kejadian lain.
dan sebaliknya.
Apabila kejadian dependent, maka konsep probabilitas bersyarat
digunakan untuk menentukan probabilitas dari kejadian yang berkaitan.

41. Konsep :
Lambang untuk probabilitas bersyarat adalah P(A|B).
Lambang tersebut menyatakan probabilitas kejadian A dengan
ketentuan kejadian B terjadi lebih dahulu. Besarnya probabilitas
bersyarat tersebut ditentukan dengan rumus :
P(A∩B)
P(A∤B) =
P(B)

42. Contoh1 :
Dari 240 lembar pengisian SPT untuk kelompk yang diterima oleh Kantor
Inspeksi Wilayah Y diperoleh data sbb : Kelompok industri kecil A
sebanyak 25% dari total lembar formulir, sedangkan industri sedang (D)
dan industri besar (F) yang memasukkan pengisian formulir jumlahnya
sama besar.
Dari kelompok industri kecil yang mengisi dengan benar (B) sebanyak 30
perusahaan, mengisi salah (S) 20 perusahaan dan sisanya meragukan (M).
Dari kelompok industri sedang, yang isinya meragukan (M) sebanyak 20
perusahaan, mengisi salah (S) sebanyak 30 perusahaan dan sisanya
mengisi dengan benar (B).
Dari peerusahaan besar (F) yang mengisi dengan benar (B) sebanyak 30
perusahaan, isian salah (S) sebanyak 50 perusahaan dan sisanya
meragukan (M).

43. Contoh1 :
a. Dari Informasi tersebut buatlah tabelnya.
b. P(A atau S)
c. P(F dan A)
d. P(F | M)
e. P(B | A)
f. P(A atau D atau F)
g. P(B | F)

44. Contoh 2 :
Diploma IPB melakukan penelitian terhadap kedisplinan karyawan dalam
menepati jam masuk kantor. Hasil penelitian tsb terlihat pada tabel :
Keterangan jml Karyawan (%)
tdk terlambat 70
terlambat paling lama 5 menit 20
terlambat lebih dari 5 menit 10
Diantara yang tidak terlambat 60%-nya berasal dari bagian Akademik dan
dari yang terlambat kurang dari 5 menit terdapat 9 % dari bagian yang
sama (Akademik) dan dari yang terlambat lebih dari 5 menit terdapat 50%
dari bagian yang sama (Akademik). Jika bagian Akademik dipanggil secara
acak, berapa probabilitas bahwa ia : (a) tidak terlambat, (b) terlambat
kurang dari 5 menit, (c) terlambat lebih dari 5 menit ?

45. KUMPULKAN Minggu
Depan