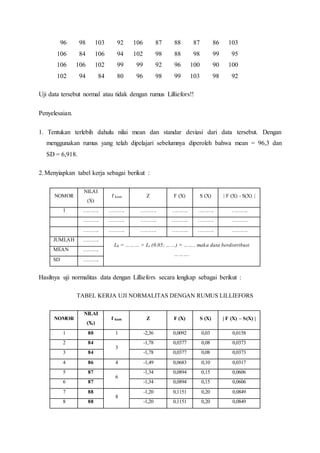
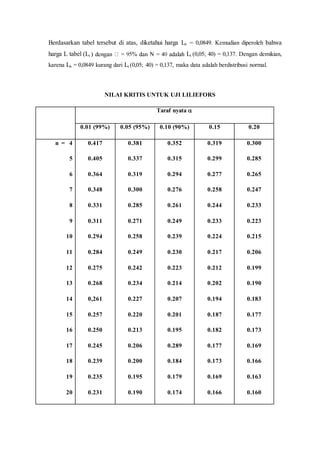
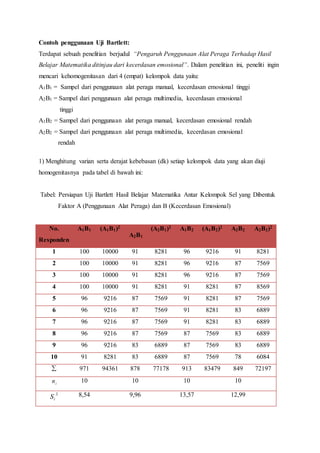
Teks tersebut membahas tentang uji normalitas dan homogenitas data. Secara singkat, uji normalitas digunakan untuk mengetahui apakah data berdistribusi normal menggunakan metode Liliefors dan Chi-Square. Uji homogenitas menguji apakah variansi antar dua kelompok data sama menggunakan uji F.

1. 1.Uji Normalitas
Uji distribusi normal adalah uji untuk mengukur apakah data yang didapatkan
memiliki distribusi normal sehingga dapat dipakai dalam statistik parametrik (statistik
inferensial).
Data klasifikasi kontinue, adalah data kuantitatif yang termasuk dalam pengukuran
data skala interval atau ratio, untuk dapat dilakukan uji statistik pengukuran data skala
interval atau rasio dan uji statistik parametrik dipersyaratkan berdistribusi normal. Uji
tersebut perlu dilakukan uji normalitas terhadap data.
Pengujian normalitas dilakukan untuk mengetahui normal tidaknya suatu distribusi
data. Hal ini penting diketahui berkaitan dengan ketetapatan pemilihan uji statistik yang
akan dipergunakan. Uji parametrik misalmya, mengisyaratkan data harus berdistribusi
normal.Apabila distribusi data tidak normal maka disarankan untuk menggunakan uji
nonparametrik.
Pengujian normalitas ini harus dilakukan apabila belum ada teori yang menyatakan
bahwa variabel yang diteliti adalah normal. Tetapi, apabila telah ada teori yang menyatakan
bahwa suatu variabel yang sedang diteliti itu normal, maka tidak diperlukan lagi pengujian
normalitas data.
Berikut ini adalah metode – metode yang dapat digunakan untuk uji normalitas :
1) Metode Lilierfors
Metode Liliefors menggunakan data yang belum diolah ke dalam tabel distribusi
frekuensi.Data di transformasikan ke dalam nilai Z untuk dapat dihitung luasan kurva
normal sebagai probabilitas komulatif normal.
Kelebihan Liliefors test adalah perhitungannya yang sederhana, serta cukup kuat
(power full) sekalipun dengan ukuran sampel kecil (n = 4) (Harun Al Rasyid, 2005).
Proses pengujian Liliefors test dapat mengikuti langkah-langkah berikut:
1.Membuat tabel kerja dengan 7 kolom (sebagaimana terlampir)
2.Memasukan nilai atau skor pada tabel kerja secara berurutan

2. 3.Mencari nilai Z score, dengan rumus : Z = (Xi – Mean)/SD
4. Menentukan Nilai Z tabel {F(z)} dengan menggunakan tabel Normal Baku score
komulatif proporsi luasan kurva normal berdasarkan notasi Zi, dihitung dari luasan kurva
normal mulai dari ujung kiri kurva sampai dengan titik Zi.
5.Menentukan S(X) dengan rumus S(X) = f kum : N
6.Menghitung harga Lilliefors hitung dengan rumus : Lh = |F(X) – S(X)|
7.Mencari nilai Lilliefors terbesar sebagai Lhitung
8.Menentukan harga Lillefors tabel (Lt ) dengan rumus : (a, n)
9.Membuat kesimpulan :
a.Jika harga Lh <>t, maka data berdistribusi normal
b.Jika harga Lh > harga Lt, maka data tidak berdistribusi normal
PERSYARATAN
•Data berskala interval atau ratio (kuantitatif)
•Data tunggal / belum dikelompokkan pada tabel distribusi frekuensi
•Dapat untuk n besar maupun n kecil.
SIGNIFIKANSI
Signifikansi uji, nilai | F (x) - S (x) | terbesar dibandingkan dengan nilai tabel
Lilliefors.
Jika nilai | F (x) - S (x) | terbesar < nilai tabel Lilliefors, maka Ho diterima ; Ha
ditolak.
Jika nilai | F(x) - S(x) | terbesar > dari nilai tabel Lilliefors, maka Ho ditolak ; Ha
diterima.
Tabel Lilliefors pada lampiran, Tabel Harga Quantil Statistik Lilliefors Distribusi Normal
Contoh :
Diketahui suatu data sebagai berikut :

3. 96 98 103 92 106 87 88 87 86 103
106 84 106 94 102 98 88 98 99 95
106 106 102 99 99 92 96 100 90 100
102 94 84 80 96 98 99 103 98 92
Uji data tersebut normal atau tidak dengan rumus Lilliefors!!
Penyelesaian.
1. Tentukan terlebih dahulu nilai mean dan standar deviasi dari data tersebut. Dengan
menggunakan rumus yang telah dipelajari sebelumnya diperoleh bahwa mean = 96,3 dan
SD = 6,918.
2.Menyiapkan tabel kerja sebagai berikut :
NOMOR
NILAI
(X)
f kum Z F (X) S (X) | F (X) - S(X) |
1 ………. ………. ………. ………. ………. ……….
………. ………. ………. ………. ………. ……….
………. ………. ………. ………. ………. ……….
JUMLAH ……….
Lh = ……… > Lt (0.05; ……) = …….. maka data berdistribusi
……….
MEAN ……….
SD ……….
Hasilnya uji normalitas data dengan Lilliefors secara lengkap sebagai berikut :
TABEL KERJA UJI NORMALITAS DENGAN RUMUS LILLIEFORS
NOMOR
NILAI
(Xi)
f kum Z F (X) S (X) | F (X) – S(X) |
1 80 1 -2,36 0,0092 0,03 0,0158
2 84
3
-1,78 0,0377 0,08 0,0373
3 84 -1,78 0,0377 0,08 0,0373
4 86 4 -1,49 0,0683 0,10 0,0317
5 87
6
-1,34 0,0894 0,15 0,0606
6 87 -1,34 0,0894 0,15 0,0606
7 88
8
-1,20 0,1151 0,20 0,0849
8 88 -1,20 0,1151 0,20 0,0849

4. 9 90 9 -0,91 0,1812 0,23 0,0438
10 92
12
-0,62 0,2671 0,30 0,0329
11 92 -0,62 0,2671 0,30 0,0329
12 92 -0,62 0,2671 0,30 0,0329
13 94
14
-0,33 0,3698 0,35 0,0198
14 94 -0,33 0,3698 0,35 0,0198
15 95 15 -0,19 0,4255 0,38 0,0505
16 96
18
-0,04 0,4827 0,45 0,0327
17 96 -0,04 0,4827 0,45 0,0327
18 96 -0,04 0,4827 0,45 0,0327
19 98
23
0,25 0,5971 0,58 0,0221
20 98 0,25 0,5971 0,58 0,0221
21 98 0,25 0,5971 0,58 0,0221
22 98 0,25 0,5971 0,58 0,0221
23 98 0,25 0,5971 0,58 0,0221
24 99
27
0,39 0,6518 0,68 0,0232
25 99 0,39 0,6518 0,68 0,0232
26 99 0,39 0,6518 0,68 0,0232
27 99 0,39 0,6518 0,68 0,0232
28 100
29
0,53 0,7036 0,73 0,0214
29 100 0,53 0,7036 0,73 0,0214
30 102
32
0,82 0,7950 0,80 0,0050
31 102 0,82 0,7950 0,80 0,0050
32 102 0,82 0,7950 0,80 0,0050
33 103
35
0,97 0,8336 0,88 0,0414
34 103 0,97 0,8336 0,88 0,0414
35 103 0,97 0,8336 0,88 0,0414
36 106
40
1,40 0,9196 1,00 0,0804
37 106 1,40 0,9196 1,00 0,0804
38 106 1,40 0,9196 1,00 0,0804
39 106 1,40 0,9196 1,00 0,0804
40 106 1,40 0,9196 1,00 0,0804
JUMLAH 3852
Lh = 0.0849 < Lt (0.05; 40) = 0.137 maka data berdistribusi normalMEAN 96,3
SD 6,918

5. Berdasarkan tabel tersebut di atas, diketahui harga Lh = 0,0849. Kemudian diperoleh bahwa
harga L tabel (Lt Lt (0,05; 40) = 0,137. Dengan demikian,
karena Lh = 0,0849 kurang dari Lt (0,05; 40) = 0,137, maka data adalah berdistribusi normal.
NILAI KRITIS UNTUK UJI LILIEFORS
Taraf nyata 
0.01 (99%) 0.05 (95%) 0.10 (90%) 0.15 0.20
n = 4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0.417
0.405
0.364
0.348
0.331
0.311
0.294
0.284
0.275
0.268
0,261
0.257
0.250
0.245
0.239
0.235
0.231
0.381
0.337
0.319
0.300
0.285
0.271
0.258
0.249
0.242
0.234
0.227
0.220
0.213
0.206
0.200
0.195
0.190
0.352
0.315
0.294
0.276
0.261
0.249
0.239
0.230
0.223
0.214
0.207
0.201
0.195
0.289
0.184
0.179
0.174
0.319
0.299
0.277
0.258
0.244
0.233
0.224
0.217
0.212
0.202
0.194
0.187
0.182
0.177
0.173
0.169
0.166
0.300
0.285
0.265
0.247
0.233
0.223
0.215
0.206
0.199
0.190
0.183
0.177
0.173
0.169
0.166
0.163
0.160

6. 25
30
n > 30
0.200
0.187
(1.031)/√n
0.173
0.161
(0.886)/√n
0.158
0.144
(0.805)/√n
0.147
0.136
(0.768)/√n
0.142
0.131
(0.736)/√n
2. Metode Chi-Square
Metode Chi-Square atau X2 untuk Uji Goodness of fit Distribusi Normal,menggunakan
pendekatan penjumlahan penyimpangan data observasi tiap kelasdengan nilai
yang diharapkan.
𝑋2
= ∑
( 𝑋 𝑋−𝑋 𝑋)
𝑋 𝑋
Keterangan :
X2 = Nilai X2
Oi = Nilai observasi
Ei = Nilai expected / harapan, luasan interval kelas berdasarkan tabel normal dikalikan N
(total frekuensi) ≈ pi x N
N = Banyaknya angka pada data (total frekuensi)
Komponen penyusun rumus tersebut di atas didapatkan berdasarkan
padahasil transformasi data distribusi frekuensi yang akan diuji
normalitasnya, sebagai berikut :

7. Keterangan :
Xi = Batas tidak nyata interval kelas
Z = Transformasi dari angka batas interval kelas ke notasi pada distribusi normal
pi = Luas proporsi kurva normal tiap interval kelas berdasar tabel normal
Oi = Nilai observasi
Ei = Nilai expected / harapan, luasan interval kelas berdasarkan tabel normal dikalikan N
(total frekuensi) ≈ pi x N
PersyaratanMetode Chi Square (Uji Goodness of fit Distribusi Normal) :
• Data tersusun berkelompok atau dikelompokkan dalam tabel distribus frekuensi.
• Cocok untuk data dengan banyaknya angka besar ( n > 30 )
Signifikansi :
Signifikansi uji, nilai X2 hitung dibandingkan dengan X2 tabel (Chi-Square).
Jika nilai X2 hitung < nilai X2 tabel, maka Ho diterima ; Ha ditolak.
Jika nilai X2 hitung > nilai X2 tabel, maka maka Ho ditolak ; Ha diterima.
Contoh :
Pelemparan dadu sebanyak 120 kali menghasilkan data sebagai berikut :
*) Nilai dalam kotak kecil adalah frekuensi ekspektasi
Apakah dadu itu dapat dikatakan setimbang?
Lakukan pengujian dengan taraf nyata = 5 %
Solusi :

8. 1. Ho : Dadu setimbang → semua sisi akan muncul = 20 kali.
Hi : Dadu tidak setimbang → ada sisi yang muncul ≠20 kali.
2. Statistik Uji χ²
3. Nilai α = 5 % = 0.05
k = 6 ; db = k - 1 = 6-1 = 5
4. Nilai Tabel χ²
k = 6 ; db = k - 1 = 6-1 = 5
db = 5;α = 0.05 → χ² tabel = 11.0705
5. Wilayah Kritis = Penolakan H0 jika χ² hitung > χ² tabel (db; α)
χ² hitung > 11.0705
6. Perhitungan χ²
𝑋2
= ∑
( 𝑋 𝑋−𝑋 𝑋)
𝑋 𝑋
Gunakan tabel agar lebih sistematis :
7. Kesimpulan :
χ² hitung = 1.70 < χ² tabel
Nilai χ² hitung ada di daerah penerimaan Ho
Ho diterima; pernyataan dadu setimbang dapat diterima.

9. B. HOMOGENITAS
Pengujian homogenitas adalah pengujian mengenai sama tidaknya variansi-variansi
dua buah distribusi atau lebih. Uji homogenitas dilakukan untuk mengetahui apakah data
dalam variabel X dan Y bersifat homogen atau tidak.
1. Uji Homogenitas Variansi ( Uji F)
Uji Homogenitas Variansi ( Uji F) digunakan hanya pada 2 kelompok data.
Langkah-langkah menghitung uji homogenitas :
a. Mencari Varians atau Standar deviasi Variabel X danY, dengan rumus :
b. . Mencari F hitung dengan dari varians X danY, dengan rumus :
c. Membandingkan Fhitung dengan Ftabel pada tabel distribusi F, dengan
untuk varians terbesar adalah dk pembilang n-1
untuk varians terkecil adalah dk penyebut n-1
Jika Fhitung < Ftabel, berarti homogen
Jika Fhitung > Ftabel, berarti tidak homogen
Contoh penggunaan Uji Fisher:
Terdapat sebuah penelitian berjudul “Pengaruh Penggunaan Alat Peraga Terhadap Hasil
Belajar Matematika”. Dalam penelitian ini, peneliti ingin mencari kehomogenitasan dari
variabel bebas antara penggunaan alat peraga manual sebagai kelas eksperimen terhadap
penggunaan alat peraga multimedia sebagai kelas kontrol. Perhitunganya mengacu kepada
langkah-langkah di atas, adalah sebagai berikut:
1) Menghitung varian kedua kelompok data:
)1(
)(. 22
2



 
nn
xxn
Sx
)1(
)(. 22
2



 
nn
YYn
SY
kecil
besar
hitung
S
S
F 

10. Tabel: Data Uji Fisher Hasil Belajar Matematika Antar Kolom Penggunaan Alat Peraga
Manual (X) dan Alat Peraga Multimedia (Y)
Dari data diatas didapat :
)1(
)(. 22
2



 
nn
xxn
Sx
)120(20
)1884(177840.20 2



380
7344

326,19
Sx = 4,396
)1(
)(. 22
2



 
nn
YYn
SY
)120(20
)1727(149375.20 2



380
4971

081,13

11. SY = 3,616
2) Menghitung nilai Fhitung
kecil
besar
hitung
S
S
F 
616,3
396,4

= 1,215
3) Menentukan Ftabel :
Dengan dk pembilang = 20 – 1= 19 (untuk varian terbesar) dan dk penyebut = 20 – 1= 19
(untuk varian terkecil), serta taraf signifikansi (𝛼) = 0,05 maka diperoleh Ftabel = 2,15
4) Bandingkan Fhitung dengan Ftabel :
Ternyata Fhitung < Ftabel = 1,215 < 2,15 maka Ho diterima dan disimpulkan kedua
kelompok data memiliki varian yang sama atau homogen.
2. Uji Bartlett
Uji Bartlett digunakan pada data lebih dari 2 kelompok data.
Misalkan sampel berukuran n1,n2,…,ni dengan data Yij = (I = 1,2,…,k dan j = 1,2,…,nk) dan
hasil pengamatan telah disusun seperti dalam Tabel dibawah ini. selanjutnya sampel-sampel
dhitung variansnya masing-masing yaitu S1
2, S2
2, …, Si2
Untuk mempermudah perhitungan, satuan-satuan yang diperlukan uji bartlett lebih baik
disusun dalam sebuah tabel sebagai berikut :

12. Dari tabel diatas hitung nilai-nilai yang dibutuhkan :
 Varians gabungan dari semua sampel
 Harga satuan B dengan rumus
Uji bartlett digunakan statistik chi-kuadrat yaitu :
Dengan ln 10 = 2.3026
Signifikansi
Jika maka Ho ditolak
Jika maka Ho diterima
Dimana jika didapatkan dari tabel distribusi chi-kuadrat dengan peluang
(1 - ∝) dan dk = (k – 1)





)1(
)1( 2
2
n
Sn
S
ii
 dkSB )(log 2
22
log){10(ln iSdkBX 
)1)(1(
22
 khitung 
  )1(1
22
 khitung 
  112
 k

13. Contoh penggunaan Uji Bartlett:
Terdapat sebuah penelitian berjudul “Pengaruh Penggunaan Alat Peraga Terhadap Hasil
Belajar Matematika ditinjau dari kecerdasan emosional”. Dalam penelitian ini, peneliti ingin
mencari kehomogenitasan dari 4 (empat) kelompok data yaitu:
A1B1 = Sampel dari penggunaan alat peraga manual, kecerdasan emosional tinggi
A2B1 = Sampel dari penggunaan alat peraga multimedia, kecerdasan emosional
tinggi
A1B2 = Sampel dari penggunaan alat peraga manual, kecerdasan emosional rendah
A2B2 = Sampel dari penggunaan alat peraga multimedia, kecerdasan emosional
rendah
1) Menghitung varian serta derajat kebebasan (dk) setiap kelompok data yang akan diuji
homogenitasnya pada tabel di bawah ini:
Tabel: Persiapan Uji Bartlett Hasil Belajar Matematika Antar Kelompok Sel yang Dibentuk
Faktor A (Penggunaan Alat Peraga) dan B (Kecerdasan Emosional)
No.
Responden
A1B1 (A1B1)2
A2B1
(A2B1)2 A1B2 (A1B2)2 A2B2 A2B2)2
1 100 10000 91 8281 96 9216 91 8281
2 100 10000 91 8281 96 9216 87 7569
3 100 10000 91 8281 96 9216 87 7569
4 100 10000 91 8281 91 8281 87 8569
5 96 9216 87 7569 91 8281 87 7569
6 96 9216 87 7569 91 8281 83 6889
7 96 9216 87 7569 91 8281 83 6889
8 96 9216 87 7569 87 7569 83 6889
9 96 9216 83 6889 87 7569 83 6889
10 91 8281 83 6889 87 7569 78 6084
 971 94361 878 77178 913 83479 849 72197
in 10 10 10 10
2
iS 8,54 9,96 13,57 12,99

14. 2) Buat tabel penolong untuk menentukan harga-harga yang diperlukan dalam uji Bartlett:
Tabel : Perhitungan Uji Bartlett Hasil Belajar Matematika Antar Kelompok Sel yang
Dibentuk Faktor A (Penggunaan Alat Peraga) B (Kecerdasan Emosional)
Kel.
Sampel
dk Si
2 log Si
2 (dk) log
Si
2
dk. Si
2
A1B1 9 8.54 0.9317 8.3852 76.9
A2B1 9 9.96 0.9981 8.9826 89.6
A1B2 9 13.57 1.1325 10.192 122.1
A2B2 9 12.99 1.1136 10.022 116.9
 36 37,582 405,5
3) Hitung varians gabungan dari semua kelompok sampel:





)1(
)1( 2
2
i
ii
n
Sn
S
9999
)99,12(9)57,13(9)96,9(9)54,8(92


S
36
54,4052
S
= 11,265
4) Hitung harga logaritma varians gabungan dan harga satuan B:
log S2 = log 11,265 = 1,05
dan B = (log S2) (Σ dk) = 1,05 . 36 = 37,86
5) Hitung nilai chi-kuadrat ( hitung
2
 ) :
}log)(){10(ln 22
ihitung SdkB 
= (2,3026)( 37,86 - 37,582)
= ( 2,30265)(0,278)
= 0,64
6) Tentukan harga chi-kuadrat tabel pada taraf nyata 𝛼=0,05 dan derajat kebebasan
(dk) = k – 1 = 3, yaitu = = 7,815
Menguji hipotesis homogenitas data dengan cara membandingkan nilai hitung
2
 dan tabel
2

Ternyata hitung
2
 < tabel
2
 = 0,64 < 7,815 maka Ho diterima dan disimpulkan keempat
kelompok data memiliki varian yang sama atau homogen.
)( 2
tabel
tabel
2
   112
 k