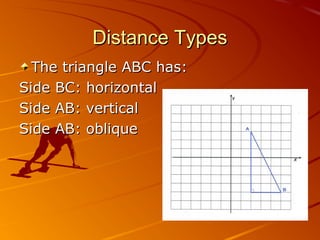
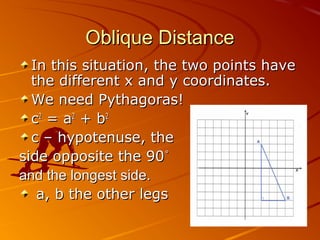
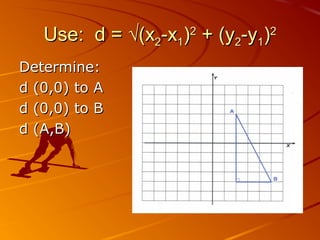
This document discusses different methods for calculating distance in the Cartesian plane. It introduces horizontal, vertical, and oblique (diagonal) distance. Horizontal distance is found by subtracting the x-coordinates of two points, vertical by subtracting the y-coordinates, and oblique distance uses the Pythagorean theorem. The distance formula is also provided as a method to find the distance between any two points by taking the square root of the sum of the differences of the x-coordinates and y-coordinates squared. The document also covers finding the midpoint between two points by taking the average of the x-coordinates and y-coordinates.

1. Finding Distance in theFinding Distance in the
Cartesian PlaneCartesian Plane
The Cartesian PlaneThe Cartesian Plane
is the x-y Graph!is the x-y Graph!

2. Distance Between 2 PointsDistance Between 2 Points
Distance between points can beDistance between points can be
determined for the 3 cases:determined for the 3 cases:
Horizontal distanceHorizontal distance
Vertical distanceVertical distance
Oblique (diagonal distance)Oblique (diagonal distance)
N.B. Distance is always positive.N.B. Distance is always positive.

3. Distance TypesDistance Types
The triangle ABC has:The triangle ABC has:
Side BC: horizontalSide BC: horizontal
Side AB: verticalSide AB: vertical
Side AB: obliqueSide AB: oblique

4. Horizontal DistanceHorizontal Distance
In this situation, the two points haveIn this situation, the two points have
the same y coordinate, so to find thethe same y coordinate, so to find the
distance, subtract the x coordinates.distance, subtract the x coordinates.
E.g (8,0) – (4,0) = 4E.g (8,0) – (4,0) = 4
E.g.(8,1) – (-4,1) = 8 - -4 = 12E.g.(8,1) – (-4,1) = 8 - -4 = 12

5. Vertical DistanceVertical Distance
In this situation, the two points haveIn this situation, the two points have
the same x coordinate, so to find thethe same x coordinate, so to find the
distance, subtract the y coordinates.distance, subtract the y coordinates.
E.g (0,7) – (0,3) = 4E.g (0,7) – (0,3) = 4
E.g.(8,1) – (8,-2) = 1--2 = 3E.g.(8,1) – (8,-2) = 1--2 = 3

6. Vertical/Horizontal DistanceVertical/Horizontal Distance

7. Oblique DistanceOblique Distance
In this situation, the two points haveIn this situation, the two points have
the different x and y coordinates.the different x and y coordinates.
We need Pythagoras!We need Pythagoras!
cc22
= a= a22
+ b+ b22
c – hypotenuse, thec – hypotenuse, the
side opposite the 90side opposite the 90˚˚
and the longest side.and the longest side.
a, b the other legsa, b the other legs

8. Pythagoras to the Rescue!Pythagoras to the Rescue!
AB hypotenuseAB hypotenuse
AC, BC legsAC, BC legs
AC = 7 squaresAC = 7 squares
BC = 3 squaresBC = 3 squares
AB = how long?AB = how long?

9. Distance FormulaDistance Formula
The distance between two points canThe distance between two points can
be found using the distance formula.be found using the distance formula.
The distance between (The distance between (xx11,, yy11) and () and (xx22,,
yy22) is given by:) is given by:
Distance, d =Distance, d = √(x√(x22-x-x11))22
+ (y+ (y22-y-y11))22

10. Use: d =Use: d = √(x√(x22-x-x11))22
+ (y+ (y22-y-y11))22
Determine:Determine:
d (0,0) to Ad (0,0) to A
d (0,0) to Bd (0,0) to B
d (A,B)d (A,B)

11. Midpoint of a LineMidpoint of a Line
Given 2 points (xGiven 2 points (x11, y, y11) and (x) and (x22,y,y22) the) the
middle point or “midpoint” can bemiddle point or “midpoint” can be
determined by the following:determined by the following:
Midpoint (x,y) = (Midpoint (x,y) = (xx11+x+x22,, yy11+y+y22))
2 22 2
Find the midpoint of (5,7) & (11,29)Find the midpoint of (5,7) & (11,29)
Find the midpoint of (-3,-5) & (17, 12)Find the midpoint of (-3,-5) & (17, 12)

12. Exam QuestionExam Question
To service a new residential development, the town surveyor has drawn on a Cartesian plane the
new part of the water main that must be constructed.
represents the existing water main.
and represent the new water main, where M is the midpoint of
Rounded to the nearest tenth, what is the total length of the new water main FGM?
Show all your work.

13. ActivitiesActivities
P.152P.152
Questions 1abcd, 2, 3 ,7Questions 1abcd, 2, 3 ,7