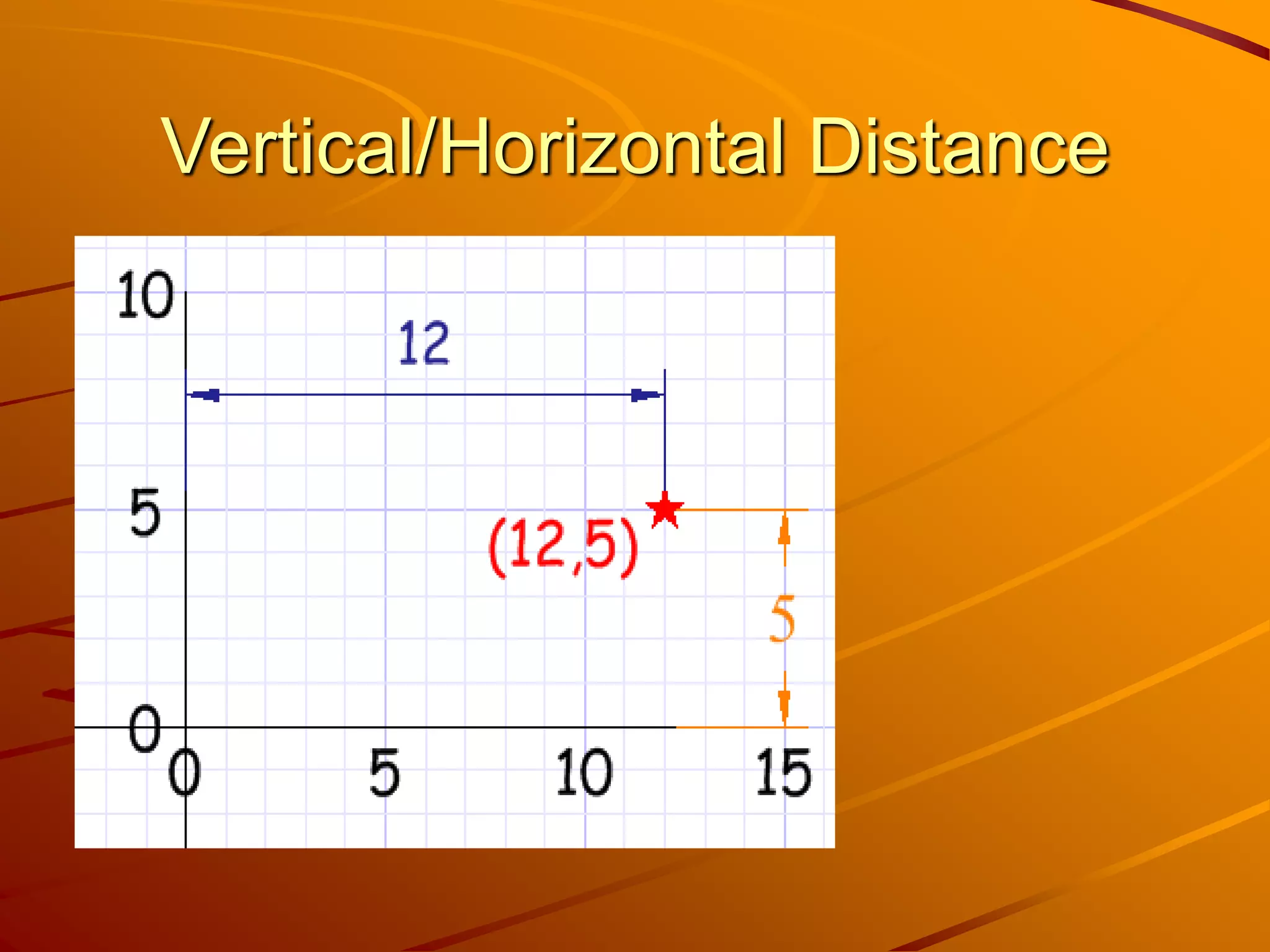
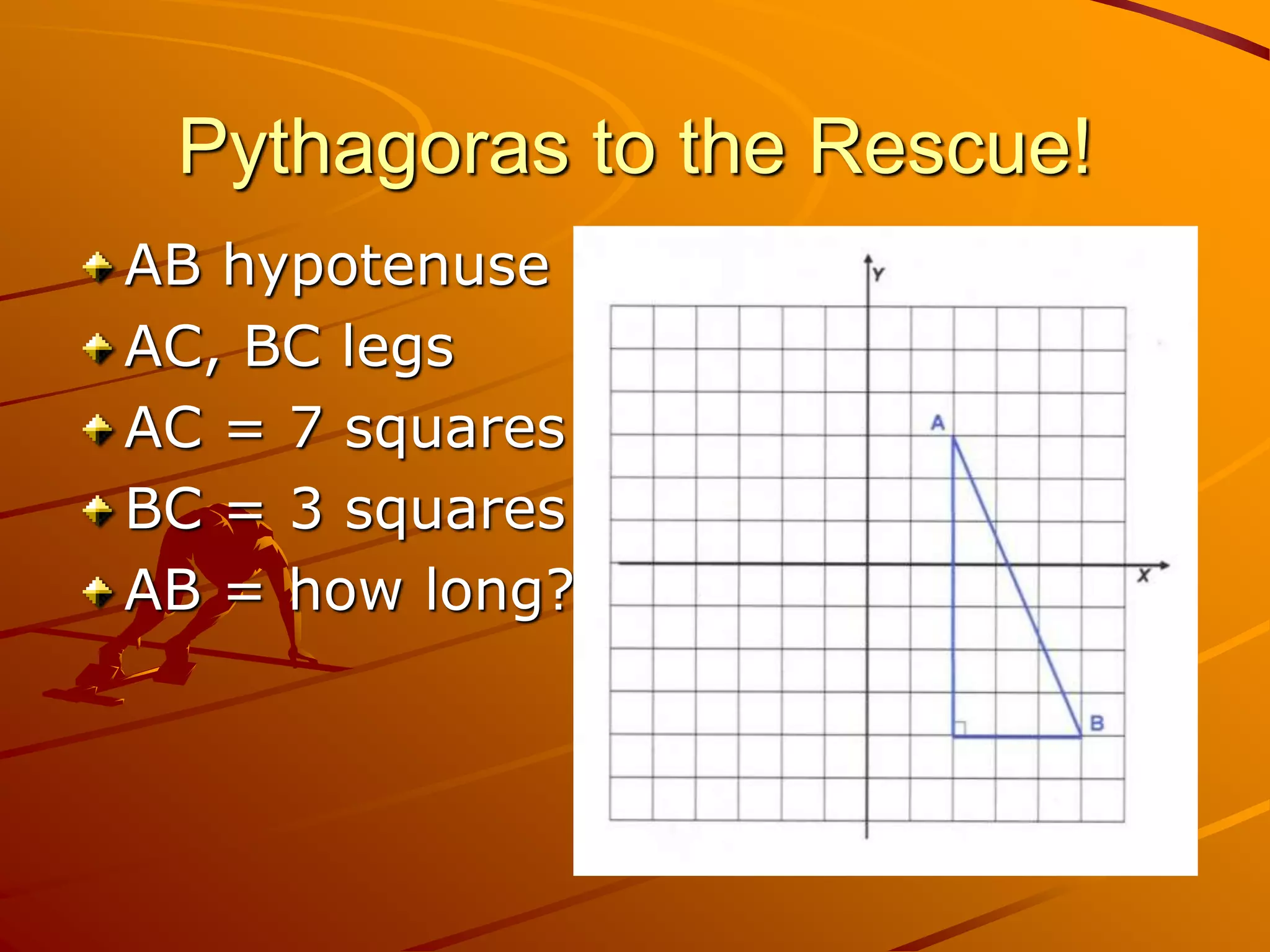
The document summarizes key concepts about finding distance in the Cartesian plane. It outlines three cases for distance between two points: horizontal, vertical, and oblique (diagonal) distance. It then explains how to calculate each type of distance and introduces the distance formula. The Pythagorean theorem is used to calculate oblique distance. Additional topics covered include finding the midpoint between two points, solving problems involving equidistant points, and the relationship between distance and parabolas.

1. Finding Distance in the
Cartesian Plane
The Cartesian Plane
is the x-y Graph!

2. Distance Between 2 Points
Distance between points can be
determined for the 3 cases:
Horizontal distance
Vertical distance
Oblique (diagonal distance)
N.B. Distance is always positive.

3. Distance Types
The triangle ABC has:
Side BC: horizontal
Side AB: vertical
Side AB: oblique

4. Horizontal Distance
In this situation, the two points have
the same y coordinate, so to find the
distance, subtract the x coordinates.
E.g (8,0) – (4,0) = 4
E.g.(8,1) – (-4,1) = 8 - -4 = 12

5. Vertical Distance
In this situation, the two points have
the same x coordinate, so to find the
distance, subtract the y coordinates.
E.g (0,7) – (0,3) = 4
E.g.(8,1) – (8,-2) = 1--2 = 3

6. Vertical/Horizontal Distance

7. Oblique Distance
In this situation, the two points have
the different x and y coordinates.
We need Pythagoras!
c2 = a2 + b2
c – hypotenuse, the
side opposite the 90˚
and the longest side.
a, b the other legs

8. Pythagoras to the Rescue!
AB hypotenuse
AC, BC legs
AC = 7 squares
BC = 3 squares
AB = how long?

9. Distance Formula
The distance between two points can
be found using the distance formula.
The distance between (x1, y1) and
(x2, y2) is given by:
Distance, d = √(x2-x1)2 + (y2-y1)2

10. Use: d = √(x2-x1)2 + (y2-y1)2
Determine:
d (0,0) to A
d (0,0) to B
d (A,B)

11. Activities
p.241
Do Questions 1,2,5

12. Midpoint of a Line
Given 2 points (x1, y1) and (x2,y2) the
middle point or “midpoint” can be
determined by the following:
Midpoint (x,y) = (x1+x2, y1+y2)
2 2
Find the midpoint of (5,7) & (11,29)
Find the midpoint of (-3,-5) & (17, 12)

13. Exam Question
To service a new residential development, the town surveyor has drawn on a Cartesian plane the
new part of the water main that must be constructed.
DE represents the existing water main.
FG and GM represent the new water main, where M is the midpoint of DE
1
1
M
D(0, 4)
E(3, -2)
F(-3, -4)
G(-5, -1)
y
x
Rounded to the nearest tenth, what is the total length of the new water main FGM?
Show all your work.

14. Activity
Do Q. 8 on p. 243.
Find the midpoint twice.

15. Activity: Oddball Problems
D Q. 11a,b on page 244.
Sketch a diagram.
Construct the following
chart.
Calculate the hypotenuse
c using Pythagoras.
Did you get an answer?
a
Mary
b
Anthony
c
Distance
3 5
3 6
5 5
5 4

16. Response
Set the beach distance for Mary to
be x.
The distance for Anthony is 10-x.
The distance for both is c and is
equal – as stated in the question.
Set up the equivalent equations:
c2 = a2 + b2 (Mary) = a2 + b2 (Tony)
32 + x2 = 52 + (10-x)2

17. Response
You should have got x = 5.8
Now what is the distance they both
travel?
Are the distances equal?
Finish 11 c,d

18. Equidistant Points
To find a point equidistant (means
equal distance!), we can use the
same distance formula TWICE!
E.g. Find a point C on the x axis that
is equidistant from A(1,2) and B
(5,8).
So point C is (x,0) – because it is on
the x axis.

19. Equidistant Point
d(A,C) = d(B,C)
√(x2-x1)2+(y2-y1)2=√(x2-x1)2+(y2-y1)2
√(x-1)2 + (0-2)2 = √(x-5)2 + (0-8)2
Square both sides:
(x-1)2 + (0-2)2 = (x-5)2 + (0-8)2
Simplifying we get:
x2-2x + 5 = x2 -10x + 89
So -2x + 5 = -10x + 89
Finally x = 10.5
So C (10.5, 0)

20. Activity
Take a piece of 8”x11” paper.
Fold it in half lengthwise.
Fold it twice more upon itself lengthwise.
Open the sheet up, and draw straight lines along
the paper folds.
On the middle line mark a point, F, anywhere.
Fold the sheet so that the bottom of the middle
line touches point F.
Fold the sheet so that the bottom of the
remaining lines touch point F.
Mark the spot, L, along each line where the paper
has folded, the top fold only.
What do you see?

21. Distance and Parabolas
A parabola is a curve formed by all
points that are equidistant from a
line, the Directrix, and a point
outside of this line.
This point outside of the line is called
the focus of the parabola.
Each point on the line is a locus, or
location.

22. Distance and Parabolas
Measure the distance of the focus to
the vertex.
Measure the distance of the vertex to
the Directrix just below it.
What do you notice?
Do the same for any point L along
the parabola.
What do you notice?

23. Activities
P.241
Questions 4, 6, 7, 13