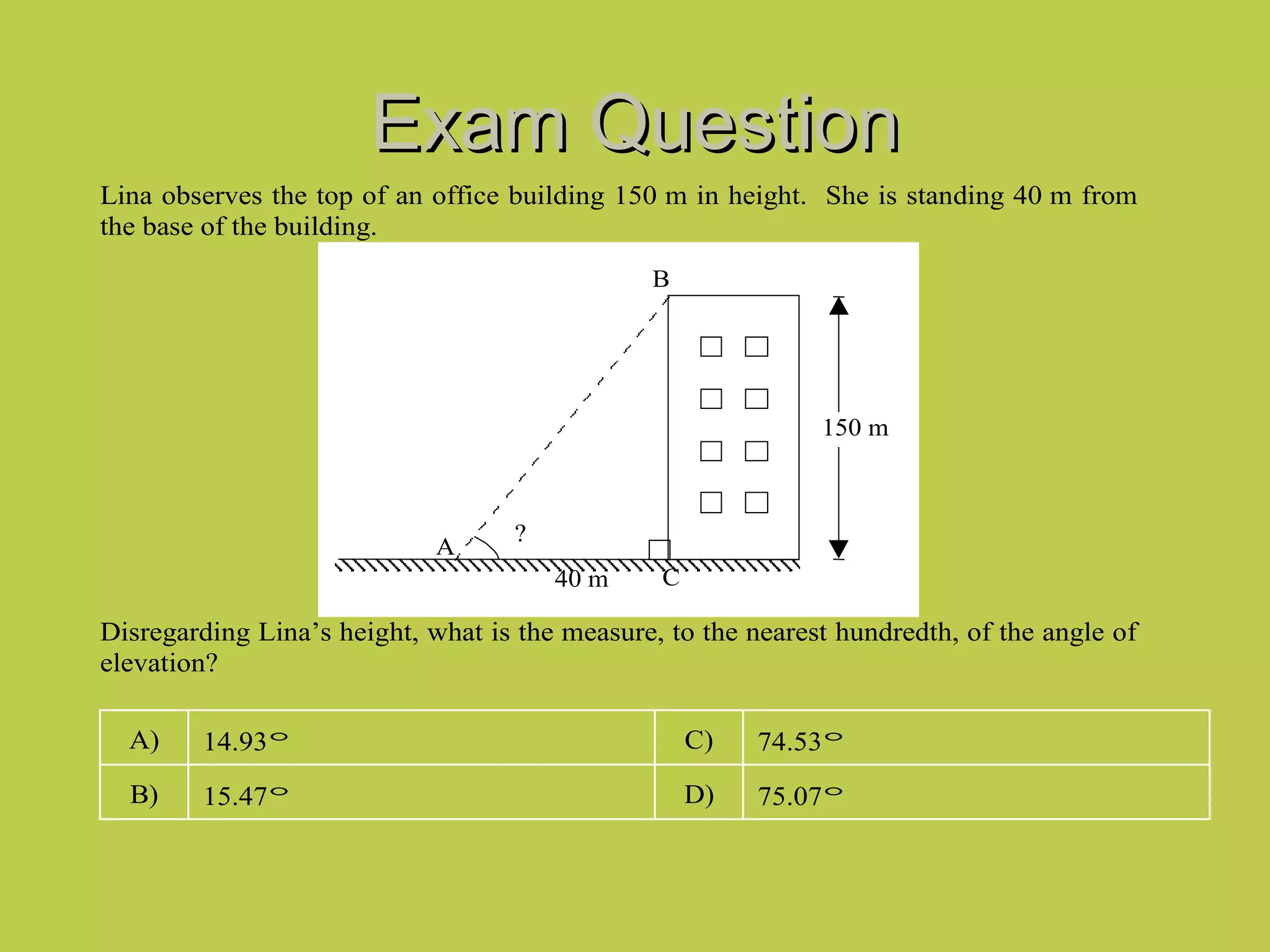
The document provides information about trigonometric ratios, identities, and laws including SOHCAHTOA, sine, cosine, and tangent functions. It also contains example problems and solutions using trigonometric ratios to solve for missing side lengths and angles in right triangles and applying the sine and cosine laws to solve for sides and angles in non-right triangles. Several exam questions are presented relating to using trigonometric functions and identities to calculate angles and distances based on information provided in diagrams of triangles.

1. Trig FunctionsTrig Functions
SOHCAHTOA and Beyond!SOHCAHTOA and Beyond!

2. Trig IdentitiesTrig Identities
 RatiosRatios
 sinA =sinA =oppopp == oo
hyp hhyp h
 cosA =cosA = adjadj == aa
hyp hhyp h
 tanA =tanA = oppopp ==oo
adj aadj a
 SOHCAHTOASOHCAHTOA

3. Exam QuestionExam Question
The teacher asked his students to find the trigonometric ratio to be used to calculate the
measurement of angle A in the following right triangle.
a C
b
A
c
B
Which one of the following equations is correct?
A) sin A =
c
b
C) cos A =
c
a
B) sin A =
b
a
D) cos A =
c
b

4. TrigonometryTrigonometry
 In trig, the ratios of the side lengthsIn trig, the ratios of the side lengths
are used to determine the angles andare used to determine the angles and
vice-versa.vice-versa.
 If you have a right angle triangleIf you have a right angle triangle
with an angle A = 30°, the sidewith an angle A = 30°, the side
opposite angle A is ½ the length ofopposite angle A is ½ the length of
the hypotenuse.the hypotenuse.

5. Solving for a Side LengthSolving for a Side Length
 Given a right angle triangle ABC withGiven a right angle triangle ABC with
<BAC = 40º, and a hypotenuse of 15 cm,<BAC = 40º, and a hypotenuse of 15 cm,
what is the length of side BC?what is the length of side BC?
 Given: <A = 40,Given: <A = 40,
 hyp = 15 cmhyp = 15 cm
 BC is oppBC is opp
 Therefore use sin A = opp/hypTherefore use sin A = opp/hyp
 sin 40 = opp/15sin 40 = opp/15
 opp = 15 sin 40 = 9.64 cmopp = 15 sin 40 = 9.64 cm

6. Table of Trig ValuesTable of Trig Values
Angle AAngle A Sine ASine A Cosine ACosine A Tangent ATangent A
00˚˚
3030˚˚
4545˚˚
6060˚˚
9090˚˚

7. Other Trig RulesOther Trig Rules
 We can see that sin A = cos (90-A)We can see that sin A = cos (90-A)
 As well, sin A = sin (180-A)As well, sin A = sin (180-A)
 And cos A = cos (360-A) = cos (-A)And cos A = cos (360-A) = cos (-A)
 Tan A = sin A/cosATan A = sin A/cosA

8. Exam QuestionExam Question
The following diagram shows the position of a golfer at a certain time during a match.
6 9 12 588 591 594 597 600 m
2 m
Position after the
third shoot
Hole
Straight-
line
Tee-off
position
A
//
30
If the golfer is 2 m off the straight line path, which one of the following expressions can
be used to calculate angle A, the angle of deviation at which he must hit the ball in order
reach the hole?
A)
2
9
Asin = C)
9
2
Asin =
B)
2
9
Atan = D)
9
2
Atan =

9. Exam QuestionExam QuestionAt the moment when it is announced that the space shuttle is at a height of 11.5 km, the
angle of elevation is 75°at observation point A.
11.5 km
B
75°
A
What is the distance between the space shuttle B and the point of observation A? (to the
nearest km)
A) 3 km C) 13 km
B) 12 km D) 44 km

10. Exam QuestionExam Question
Lina observes the top of an office building 150 m in height. She is standing 40 m from
the base of the building.
A
B
C40 m
?
150 m
Disregarding Lina’s height, what is the measure, to the nearest hundredth, of the angle of
elevation?
A) 14.93° C) 74.53°
B) 15.47° D) 75.07°

11. Sine LawSine Law
 Sine Law can be used in non-rightSine Law can be used in non-right
anglesangles
 aa == b__b__
sin A sin Bsin A sin B
c
b
aB
A
C

12. Exam QuestionExam Question
Upon leaving her house, Stephanie travelled 18.0 km to the record store. On the way
back, she stopped at the daycare centre to pick up her brother. Her route is represented
by the following figure :
Record
store
House
Daycare
centre
12.4 km
34°
20°
18.0 km
Which of the following expressions can be used to calculate the distance between the
daycare centre and the record store?
A)
°
°
34sin
20sin12.4
C)
°
°
34sin
20sin18.0
B)
°
°
20sin
34sin12.4
D)
°
°
126sin
34sin18.0

13. Cosine LawCosine Law
 This is used in non-right angleThis is used in non-right angle
triangles when the sine law cannottriangles when the sine law cannot
be used.be used.
 aa22
= b= b22
+ c+ c22
- 2bc(cosA)- 2bc(cosA)

14. Exam QuestionExam Question
To find the measure of side AB in the following triangle, the measure of which angle
must be known in order to apply the cosine law?
A
B
C
125
90x
A) The measure of angle BAC only
B) The measure of angle ABC only
C) The measure of angle BCA only
D) The measure of any interior angle

15. Exam QuestionExam Question
Villages A, B and C are located at the vertices of
a triangle, as shown in the figure on the right.
A
12 km
C ? B
16 km
65°
Given the information in the diagram, what is the distance between villages B and C?
Round your answer to the nearest tenth of a kilometre.
A) 14.5 km C) 23.7 km
B) 15.4 km D) 25.7 km

16. AnswerAnswer
 aa22
= b= b22
+ c+ c22
- 2bc(cosA)- 2bc(cosA)
 aa22
= (12)= (12)22
+(16)+(16)22
–2(12)(16)(cos65)–2(12)(16)(cos65)
 aa22
= 144 + 256 - 384(0.423)= 144 + 256 - 384(0.423)
 aa22
= 400 – 162.2= 400 – 162.2
 aa22
= 237.8= 237.8
 Take square root of both sidesTake square root of both sides
 a = 15.4 kma = 15.4 km