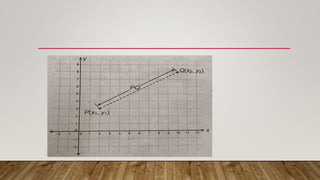
The document discusses the distance between two points. It defines distance as always being nonnegative, with a distance of zero if the points are the same and positive if they are different. It provides examples of finding the horizontal and vertical distance between points on a coordinate plane, as well as using the distance formula to calculate the distance between any two points by taking the square root of the sum of the differences of the x- and y-coordinates squared. Sample problems demonstrate applying the distance formula to find the distance between points with given coordinates.

1. DISTANCE BETWEEN
TWO POINTS
PRECIOUS FRAULEIN RODA
CASSANDRA TAGULALAP
SHAINA MAE FADERON

2. DISTANCE BETWEEN TWO POINT
The distance between two points is always nonnegative.
It is positive when the two points are different, and zero if the
points are the same. If P and Q are two points, then the
distance from P to Q is the same as the distance from Q to P.
That is, PQ = QP.
Consider two points that are aligned horizontally or
vertically on the coordinate plane. The horizontal distance
between these points is the absolute value of the difference of
their -coordinates. Likewise, the vertical distance between
these points is the absolute value of the difference of their y-
coordinates.

3. EXAMPLE 1: FIND THE DISTANCE BETWEEN P(3,2)
AND Q(10,2).
Since P and Q are aligned horizontally, then
PQ=|10-3| or PQ=7

4. EXAMPLE 2: DETERMINE THE DISTANCE BETWEEN
A(4,3) AND B(4,-5).
Points A and B are on the same vertical line. So the distance
between them is AB=|3-(-5). This can be simplified to AB
=|3+5| or AB=8.

5. THE DISTANCE FORMULA
The distance between two points, whether or not they are
aligned horizontally or vertically, can be determined using the
distance formula.
Consider the points P and Q whose coordinates are (X1, 1)
and (X2, 2), respectively. The distance d between these points can
be determined using the distance formula or

7. EXAMPLE 1: FIND THE DISTANCE BETWEEN P(1,3)
AND Q(7,11).
Solution: To find the distance between P and Q, the following
procedures can be followed.
1. Let (x1,y1) = (1,3) and (x2,y2) = (7,11).
2. Substitute the corresponding values of x1, y1, x2, and y2 in
the distance formula
3. Solve the resulting equation.
. Add a.
The distance between P and Q is 10 units.

8. EXAMPLE 2: DETERMINE THE DISTANCE BETWEEN
A(1,6) AND B(5,-2).
Solution:Let x1= 1, y1=6, x2=5, and y2= -2. Then substitute these
values in the formula

9. EXAMPLE 3:
A map showing the locations of different municipalities and
cities is drawn on a coordinate plane. Each unit on the coordinates
plane is equivalent to 6 kilometers. Suppose the coordinates of
Mabini City is (2,2) and Sta. Lucia town is (6,8). What is the shortest
distance between these two places?

10. SOLUTION:
Let x1=2, y1 =2, x2 =6, and y2 =8. Then substitute these values
into the distance formula
Simplify the expression.