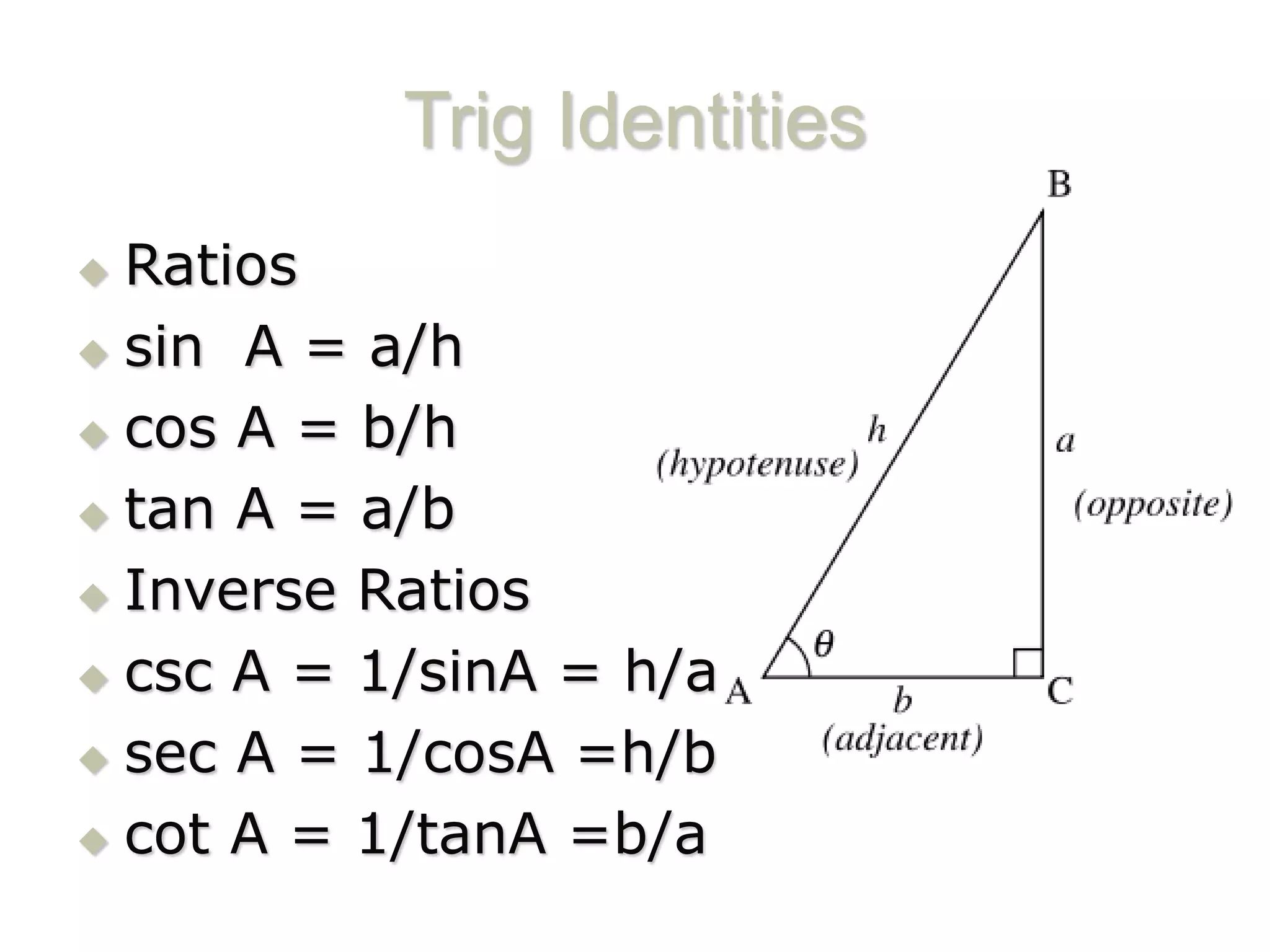
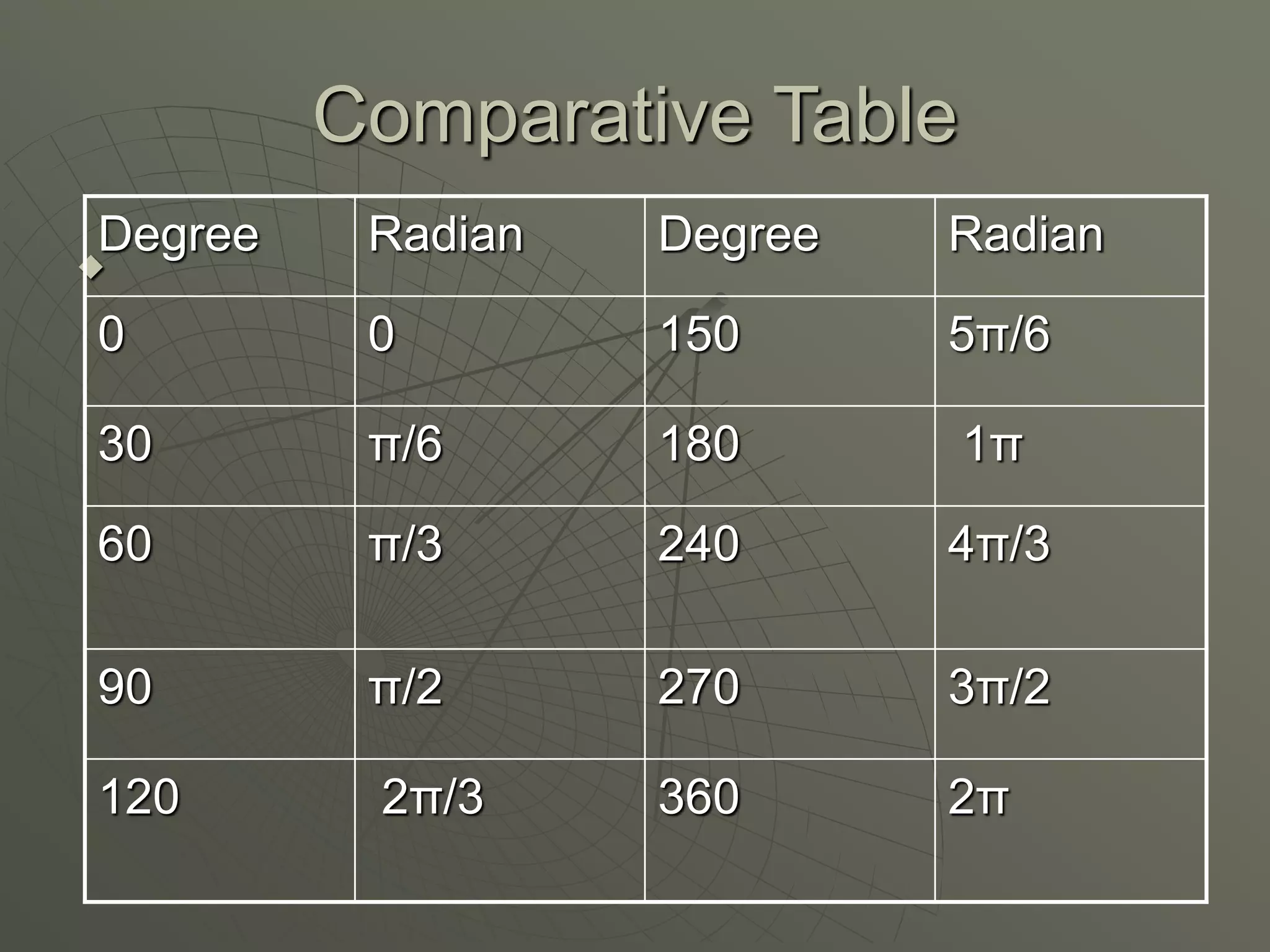
This document covers trigonometric functions including ratios, identities, and tables of trig values. It introduces radians as another way to measure angles and compares radians to degrees. Formulas are provided for converting between radians and degrees as well as calculating arc length. Examples demonstrate using radians with trig functions and finding arc lengths. The document concludes with activities involving solving problems related to trig ratios, arc measures, and conversions between radians and degrees.

1. Trig Functions
SOHCAHTOA and Beyond!
Chapter 7

2. Trig Identities
 Ratios
 sin A = a/h
 cos A = b/h
 tan A = a/b
 Inverse Ratios
 csc A = 1/sinA = h/a
 sec A = 1/cosA =h/b
 cot A = 1/tanA =b/a

3. Table of Trig Values
Angle Sine Cosine Tangent
0
30
45
60
90

4. Other Trig Rules
 We can see that sin A = cos (90-A)
 As well, sin A = sin (180-A)
 And cos A = cos (360-A) = cos (-A)
 Tan A = sin A/cosA

5. Activity
 Go to page 223, Book 2
 Do Q. 1,2,3,5,13, 17

6. Radians – That Other Mode
 Angles can be measured in terms of
degrees.
 They can also be measured in terms
of radians.
 Trigonometry often uses radians
because they are unlimited and are
treated like numbers – unlike
degrees.

7. Radians
 A radian is a unit
of angle measure
equal to the angle
formed at the
centre of a circle
by 2 radii cutting
off an arc equal to
the length of the
radius of a circle.
 About 57.295˚.

8. Radian  Degree
 The angle measure of a circle is
360˚.
 In Radians, the angle measure is 2π
radians.
 Compare: 360˚ = 6.28 = 2π
57.295˚
 So half the circumference
 = 180˚ or π radians

9. Radian Equation
 To change from degrees to radian, use the
equation:
 n = Θ
180 π radians
 where n is the angle in degrees
 where Θ is the angle in radians
 E.g. What is 90˚ in radians?
 E.g. What is 3π/2 radians in degrees?

10. Comparative Table

Degree Radian Degree Radian
0 0 150 5π/6
30 π/6 180 1π
60 π/3 240 4π/3
90 π/2 270 3π/2
120 2π/3 360 2π

11. SOHCAHTOA in Radians
 Note that if you calculate the trig
ratios of angles in radians, you get
radian based answers, but still the
same ratio.
 E.g. Sin (30˚) = 0.5
 E.g. Sin (π/6) = 0.5

12. Arc Measure: Degrees
 Arc is a portion of a circle’s
circumference.
 In the past you measured the length
of a circle’s arc using:
 Arc = n/360 x Circumference
 Arc = n/360 x π d
 E.g. What is the arc length of a 150˚
of a circle of radius 10 cm?

13. Arc Measure: Radians
 In radians, the length of an arc, L, of
a circle of radius, r, is calculated
thus:
 L = Θr
 E.g. What is the arc length of a
circle radius 15 cm with angle
measure π/6?

14. Activities: Solve
The large minute hand of a clock is 20 cm in length.
What distance will its tip move in 1 hour and 15 minutes?
A) 50 cm C) 25 cm
B) 40 cm D) 10 cm

15. Activity: Solve

Central angle AOB in the circle below measures
4
3
radians. The radius is 10 units long.
135
A
B
C
O 10
Which of the following expressions can be used to calculate the length of arc ACB?
A)



360
135
10
2
C)



360
135
102
B) 2  10  135 D)



135
360
102

16. Activity: Solve
An angle of 60 at the centre of a circle subtends an arc of
3
4
units. The radius of the circle
measures
A) 2 units C) 8 units
B) 4 units D)
15

units

17. Activity
 Worksheet p. 229: Q. 1,2,4