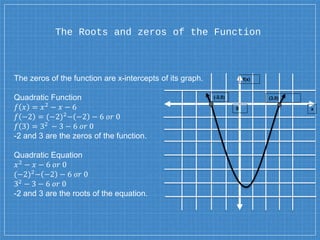
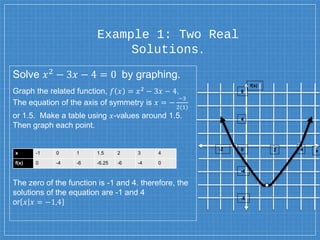
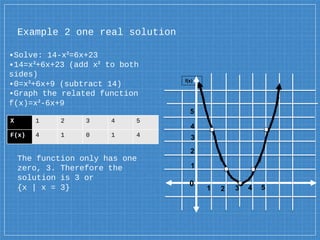
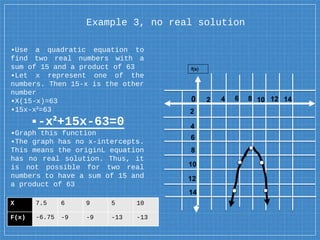
The document explains solving quadratic equations by graphing, emphasizing the standard form ax2 + bx + c = 0 and the roots or zeros of the related quadratic function. It provides examples demonstrating two real solutions, one real solution, and no real solution scenarios, illustrating how to graph the functions to find these solutions. Additionally, it includes a real-world application involving the height of a package dropped from a helicopter, showing how to determine the time it takes to reach the ground.

1. Solving Quadratic
Equations by
Graphing
Hind saed, Maryam Abbas, Marwa Nasser 10C

2. Objectives of the lesson:

3. Quadratic Equations
• Quadratic equations are quadratic
functions that re set to equal a value.
The standard form of a quadratic
equation is 𝑎𝑥2
+ bx + c = 0, where 𝑎 ≠ 0 and
𝑎, 𝑏, and 𝑐 are integers.
• The solutions of a quadratic equation
are called the roots of the equation.
One method of finding the roots of a
quadratic equation is to find the zeros
of the related quadratic function.

4. 3 solutions of quadratic
equations

5. The Roots and zeros of the Function
The zeros of the function are x-intercepts of its graph.
Quadratic Function
𝑓 𝑥 = 𝑥2 − 𝑥 − 6
𝑓 −2 = (−2)2
− −2 − 6 𝑜𝑟 0
𝑓 3 = 32 − 3 − 6 𝑜𝑟 0
-2 and 3 are the zeros of the function.
Quadratic Equation
𝑥2 − 𝑥 − 6 𝑜𝑟 0
(−2)2− −2 − 6 𝑜𝑟 0
32
− 3 − 6 𝑜𝑟 0
-2 and 3 are the roots of the equation.
(-2,0)
0
f(x)
x
(3,0)

6. Example 1: Two Real
Solutions.
Solve 𝑥2 − 3𝑥 − 4 = 0 by graphing.
Graph the related function, 𝑓 𝑥 = 𝑥2 − 3𝑥 − 4.
The equation of the axis of symmetry is 𝑥 = −
−3
2(1)
or 1.5. Make a table using 𝑥-values around 1.5.
Then graph each point.
The zero of the function is -1 and 4. therefore, the
solutions of the equation are -1 and 4
or 𝑥 𝑥 = −1,4
x -1 0 1 1.5 2 3 4
f(x) 0 -4 -6 -6.25 -6 -4 0
4
-4
2-2
8
4
-8
x
f(x)
0

7. Example 2 one real solution
▪Solve: 14-x²=6x+23
▪14=x²+6x+23 (add x² to both
sides)
▪0=x²+6x+9 (subtract 14)
▪Graph the related function
f(x)=x²-6x+9
f(x)
54321X
41014F(x)
The function only has one
zero, 3. Therefore the
solution is 3 or
{x | x = 3} 0
1 2 43 5
1
3
4
5

8. Example 3, no real solution
▪Use a quadratic equation to
find two real numbers with a
sum of 15 and a product of 63
▪Let x represent one of the
numbers. Then 15-x is the other
number
▪X(15-x)=63
▪15x-x²=63
▪-x²+15x-63=0
▪Graph this function
▪The graph has no x-intercepts.
This means the originL equation
has no real solution. Thus, it
is not possible for two real
numbers to have a sum of 15 and
a product of 63
f(x)
0 2 4 86 10
8
6
4
2
10
12
12
105967.5X
-13-13-9-9-6.75F(x)
14
14

9. Real-World Example 6: Solve by Using a Calculator.
Relief A package of supplies is tossed form a helicopter at an altitude of 200 feet. The
package’s height above the ground is modeled by 𝒉 𝒕 = −𝟏𝟔𝒕 𝟐
+ 𝟐𝟖𝒕 + 𝟐𝟎𝟎,where t
is the time in seconds after it is tossed. How long will it take the package to reach
the ground?
We need to find t when h(t) is 0. Solve 0 = −16𝑡2
+ 28𝑡 + 200.then graph the related
function 𝑓 𝑡 = −16𝑡2
+ 28𝑡 + 200 on a graphing calculator.
• Use the zero feature in the CALC menu to find the positive zero in the function, since
time cannot be negative
• Use the arrow keys to select a left bound and press Enter.
• Locate a right bound and press Enter twice.
• The positive zero of the function is about 4.52. The package would take about 4.52
seconds to reach the ground.

10. The End