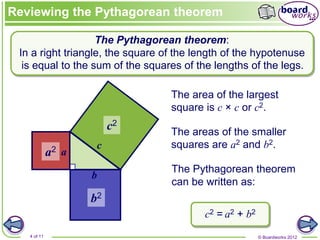
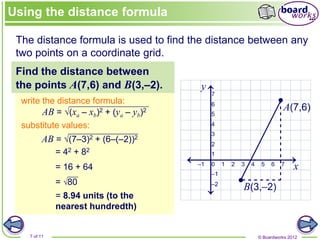
The document discusses the Cartesian coordinate system and formulas for distance, midpoint, and solving for unknown points given other point information. It provides examples of using the distance formula to calculate the distance between two points, finding the midpoint of a line segment using the average of the x- and y-coordinates, and solving for the coordinates of an unknown point if given the midpoint and one other point.

1. © Boardworks 2012
1 of 11

2. © Boardworks 2012
2 of 11
Information

3. © Boardworks 2012
3 of 11
The Cartesian coordinate system is named after the French
mathematician René Descartes (1596 – 1650).
Points in the (x, y) plane are defined by their perpendicular
distance from the x- and y-axes relative to the origin, O.
The x-coordinate gives the
horizontal distance from the
y-axis to the point.
The y-coordinate gives the
vertical distance from the
x-axis to the point.
The coordinates of a point P
are written in the form P(x, y).
The Cartesian coordinate system

4. © Boardworks 2012
4 of 11
a
c
b
The area of the largest
square is c × c or c2.
The areas of the smaller
squares are a2 and b2.
The Pythagorean theorem
can be written as:
c2 = a2 + b2
a2
c2
b2
is equal to the sum of the squares of the lengths of the legs.
The Pythagorean theorem:
In a right triangle, the square of the length of the hypotenuse
Reviewing the Pythagorean theorem

5. © Boardworks 2012
5 of 11
Given the coordinates of two points, A and B, the distance
between them is found by the Pythagorean theorem.
The distance between two points

6. © Boardworks 2012
6 of 11
What is the distance between two general points with
coordinates A(xa, ya) and B(xb, yb)?
horizontal distance between the points:
vertical distance between the points:
using the Pythagorean theorem,
the square of the distance between
the points A(xa, ya) and B(xb, yb) is:
The distance formula:
The distance formula
(xb – xa)2 + (yb – ya)2
taking the square root gives AB:
AB = √(xa – xb)2 + (ya – yb)2
yb – ya
xb – xa

7. © Boardworks 2012
7 of 11
write the distance formula:
AB = √(xa – xb)2 + (ya – yb)2
Using the distance formula
The distance formula is used to find the distance between any
two points on a coordinate grid.
Find the distance between
the points A(7,6) and B(3,–2).
= 42 + 82
= 16 + 64
= √80
= 8.94 units (to the
nearest hundredth)
AB = √(7–3)2 + (6–(–2))2
substitute values:

8. © Boardworks 2012
8 of 11
Find the lengths

9. © Boardworks 2012
9 of 11
The midpoint, M, of two points A(xa, ya) and B(xb, yb) is
mean of each coordinate of the two points:
is the mean of the
x-coordinates.
is the mean of the
y-coordinates.
Finding the midpoint
xa + xb
ya + yb
2
2

10. © Boardworks 2012
10 of 11
The midpoint of a line segment

11. © Boardworks 2012
11 of 11
–3 + a 4 + b
The midpoint of the line segment joining the point (–3, 4) to
the point P is (1, –2). Find the coordinates of the point P.
Let the coordinates of the points P be (a, b).
= (1, –2)
equating the x-coordinates:
–3 + a = 2
a = 5
equating the y-coordinates:
4 + b = –4
b = –8
The coordinates of the point P are (5, –8).
Using midpoint
midpoint formula:
–3 + a 4 + b
2 2
2
= 1
2
= –2

12. © Boardworks 2012
12 of 11
Individual Exercise:
A. Find the distance between each of the
following pairs of points. (5 points each)
1. (-5, 6) and (4, -2)
2. (8, 3) and (-5, 4)
3. (-1, 7) and (2, -1)
B. The midpoint of the line segment joining
the point (-1, 2) to the point M is (7, –1).
Find the coordinates of the point M. (10
points)