Downloaded 4,600 times
Uploaded byRoheni heni
PPT Dimensi Tiga Kelas X
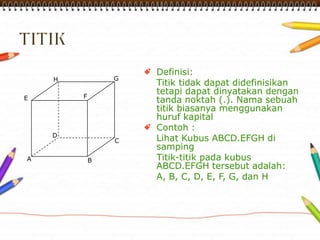
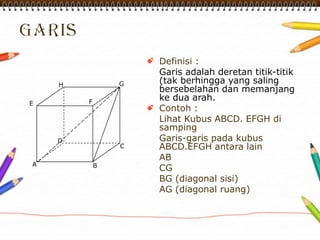
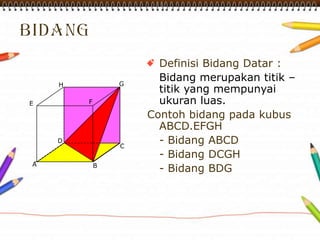
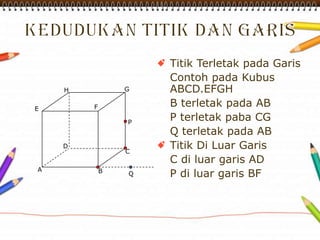
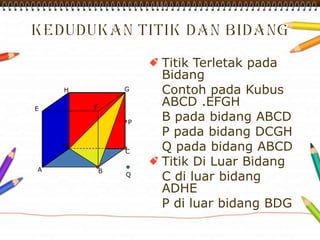
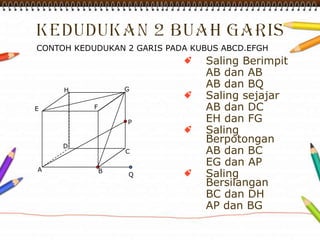
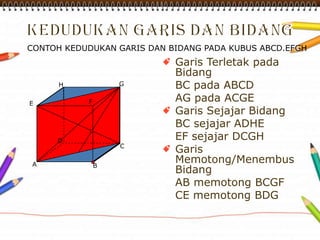
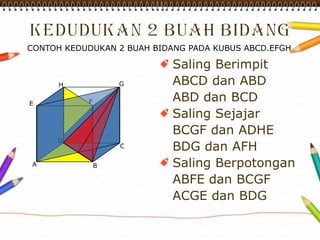
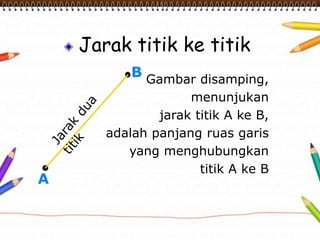
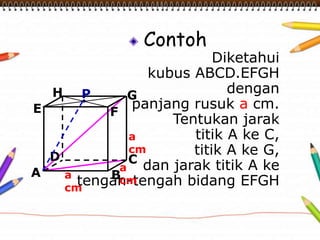
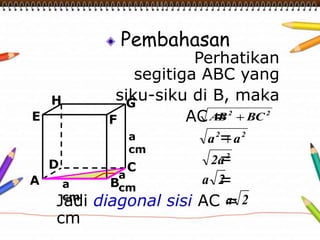
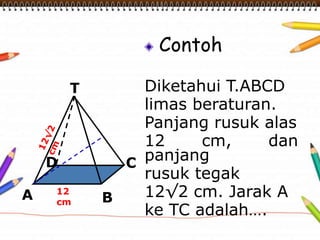
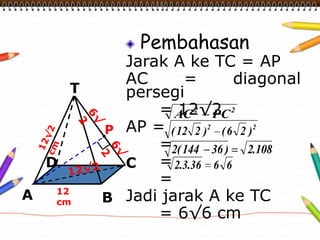
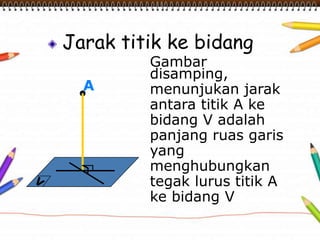
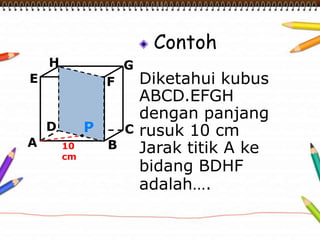
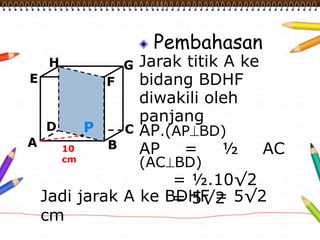
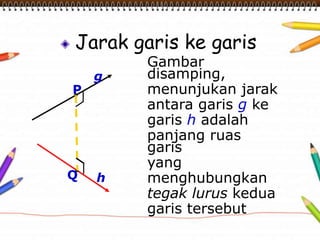
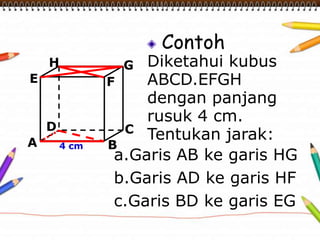
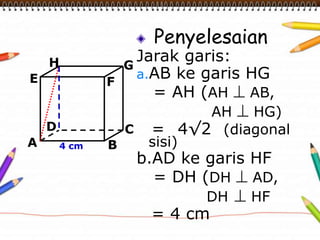
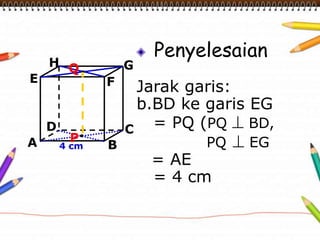
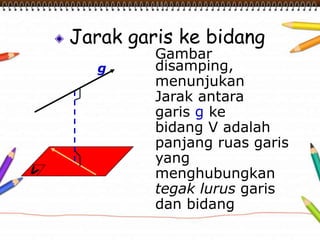
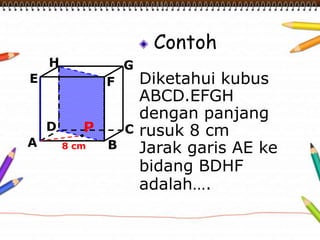
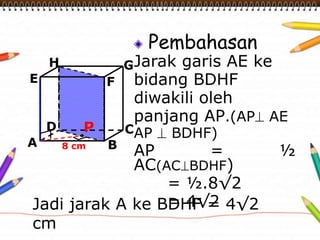
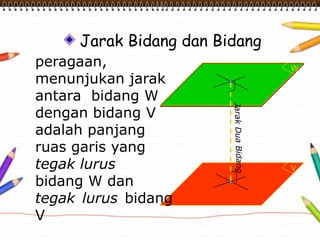
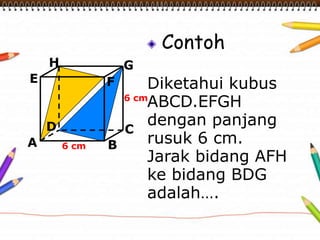
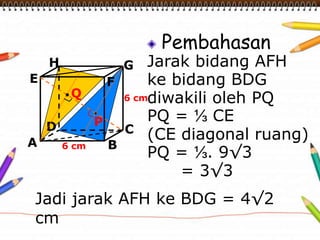
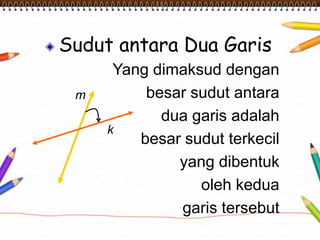
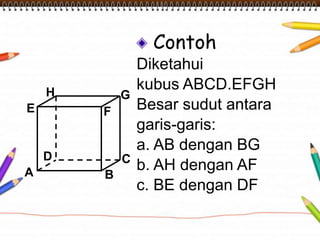
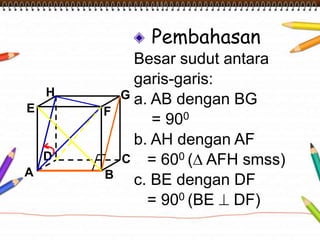
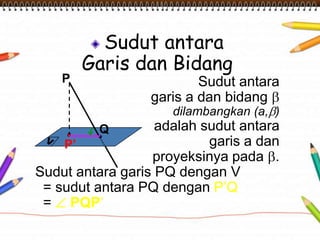
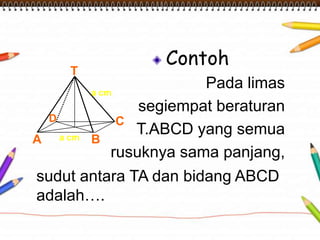
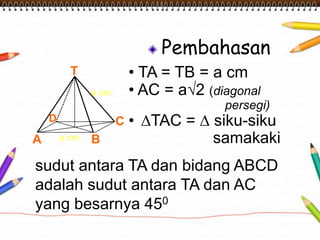
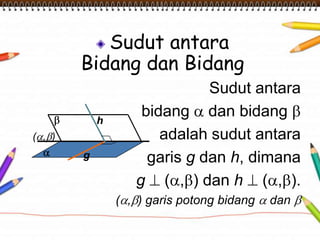
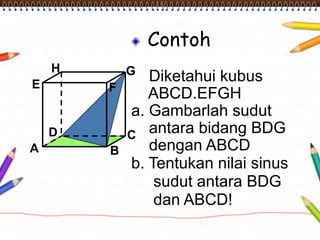
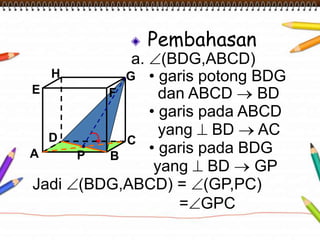
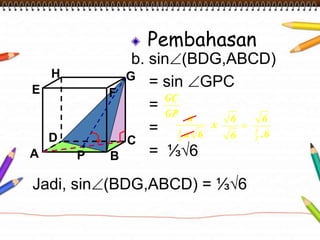
Dokumen ini membahas materi dimensi tiga untuk kelas X dengan fokus pada menentukan kedudukan, jarak, dan besar sudut yang melibatkan titik, garis, dan bidang. Penjelasan mencakup definisi dasar dari unsur-unsur geometris serta contoh-contoh perhitungan jarak dan sudut antara berbagai objek dalam ruang dimensi tiga. Materi ini bertujuan untuk meningkatkan pemahaman siswa tentang konsep-konsep geometris dalam konteks nyata.
More Related Content
Similar to PPT Dimensi Tiga Kelas X
![Modul Ajar KBC SKI Kelas 6 MI [MODULKELAS.COM]](https://cdn.slidesharecdn.com/ss_thumbnails/modulajarkbcskikelas6mimodulkelas-260207160743-753abfd0-thumbnail.jpg?width=640&height=640&fit=bounds)
PPT Dimensi Tiga Kelas X
- 1. Hany Indriani (0902138) RitaNingrum (0905926) Roheni (0902085) Rully Febrayanty (0902200)
- 2. MATERI :DIMENSI TIGA KELAS/SEMESTER: X/GANJIL
- 3. Standar Kompetensi : Menentukankedudukan, jarak, dan besar sudut yang melibatkan titik, garis, dan bidang dalam ruang dimensi tiga Kompetensi Dasar : Menentukan kedudukan titik, garis, dan bidang dalam ruang dimensi tiga Menentukan jarak dari titik ke garis dan dari titik ke bidang dalam ruang dimensi tiga Menentukan besar sudut antara garis dan bidang dan antara dua bidang dalam ruang dimensi tiga
- 4. A H G FE D C B Definisi: Titik tidakdapat didefinisikan tetapi dapat dinyatakan dengan tanda noktah (.). Nama sebuah titik biasanya menggunakan huruf kapital Contoh : Lihat Kubus ABCD.EFGH di samping Titik-titik pada kubus ABCD.EFGH tersebut adalah: A, B, C, D, E, F, G, dan H
- 5. Definisi : Garis adalahderetan titik-titik (tak berhingga yang saling bersebelahan dan memanjang ke dua arah. Contoh : Lihat Kubus ABCD. EFGH di samping Garis-garis pada kubus ABCD.EFGH antara lain AB CG BG (diagonal sisi) AG (diagonal ruang) A H G FE D C B
- 6. Definisi Bidang Datar: Bidang merupakan titik – titik yang mempunyai ukuran luas. Contoh bidang pada kubus ABCD.EFGH - Bidang ABCD - Bidang DCGH - Bidang BDG A H G FE D C B
- 7. Kedudukan Titikdan Garis Kedudukan Titik dan Bidang Kedudukan 2 buah Garis Kedudukan Garis dan Bidang Kedudukan 2 buah Bidang
- 8. Titik Terletak padaGaris Contoh pada Kubus ABCD.EFGH B terletak pada AB P terletak paba CG Q terletak pada AB Titik Di Luar Garis C di luar garis AD P di luar garis BFA H G FE D C B P Q
- 9. Titik Terletak pada Bidang Contohpada Kubus ABCD .EFGH B pada bidang ABCD P pada bidang DCGH Q pada bidang ABCD Titik Di Luar Bidang C di luar bidang ADHE P di luar bidang BDG A H G FE D C B P Q
- 10. Saling Berimpit AB danAB AB dan BQ Saling sejajar AB dan DC EH dan FG Saling Berpotongan AB dan BC EG dan AP Saling Bersilangan BC dan DH AP dan BG A H G FE D C B P Q CONTOH KEDUDUKAN 2 GARIS PADA KUBUS ABCD.EFGH
- 11. Garis Terletak pada Bidang BCpada ABCD AG pada ACGE Garis Sejajar Bidang BC sejajar ADHE EF sejajar DCGH Garis Memotong/Menembus Bidang AB memotong BCGF CE memotong BDG A H G FE D C B CONTOH KEDUDUKAN GARIS DAN BIDANG PADA KUBUS ABCD.EFGH
- 12. Saling Berimpit ABCD danABD ABD dan BCD Saling Sejajar BCGF dan ADHE BDG dan AFH Saling Berpotongan ABFE dan BCGF ACGE dan BDG A H G FE D C B CONTOH KEDUDUKAN 2 BUAH BIDANG PADA KUBUS ABCD.EFGH
- 13. Kita akan membahasjarak antara: titik ke titik titik ke garis titik ke bidang garis ke garis garis ke bidang bidang ke bidang
- 14. Jarak titik ketitik Gambar disamping, menunjukan jarak titik A ke B, adalah panjang ruas garis yang menghubungkan titik A ke B A B
- 15. Contoh Diketahui kubus ABCD.EFGH dengan panjang rusuka cm. Tentukan jarak titik A ke C, titik A ke G, dan jarak titik A ke tengah-tengah bidang EFGH A B CD H E F G a cm a cm a cm P
- 16. Pembahasan Perhatikan segitiga ABC yang siku-sikudi B, maka AC = = = = Jadi diagonal sisi AC = cm A B CD H E F G a cm a cm a cm 22 BCAB 22 aa 2 a2 2a 2a
- 17. Jarak titik keGaris A g Gambar disamping, menunjukan jarak titik A ke garis g adalah panjang ruas garis yang ditarik dari titik A dan tegak lurus garis g
- 18. Contoh Diketahui T.ABCD limas beraturan. Panjangrusuk alas 12 cm, dan panjang rusuk tegak 12√2 cm. Jarak A ke TC adalah…. 12 cm T C A B D
- 19. Pembahasan Jarak A keTC = AP AC = diagonal persegi = 12√2 AP = = = = Jadi jarak A ke TC = 6√6 cm 12 cm T C A B D P 22 PCAC 22 )26()212( 108.2)36144(2 6636.3.2
- 20. Jarak titik kebidang Gambar disamping, menunjukan jarak antara titik A ke bidang V adalah panjang ruas garis yang menghubungkan tegak lurus titik A ke bidang V A
- 21. Contoh Diketahui kubus ABCD.EFGH dengan panjang rusuk10 cm Jarak titik A ke bidang BDHF adalah…. A B CD H E F G 10 cm P
- 22. Pembahasan Jarak titik Ake bidang BDHF diwakili oleh panjang AP.(AP BD) AP = ½ AC (AC BD) = ½.10√2 = 5√2 A B CD H E F G 10 cm P Jadi jarak A ke BDHF = 5√2 cm
- 23. Jarak garis kegaris Gambar disamping, menunjukan jarak antara garis g ke garis h adalah panjang ruas garis yang menghubungkan tegak lurus kedua garis tersebut P Q g h
- 24. Contoh Diketahui kubus ABCD.EFGH dengan panjang rusuk4 cm. Tentukan jarak:A B CD H E F G 4 cm a.Garis AB ke garis HG b.Garis AD ke garis HF c.Garis BD ke garis EG
- 25. Penyelesaian Jarak garis: a.AB kegaris HG = AH (AH AB, AH HG) = 4√2 (diagonal sisi) b.AD ke garis HF = DH (DH AD, DH HF = 4 cm A B CD H E F G 4 cm
- 26. Penyelesaian Jarak garis: b.BD kegaris EG = PQ (PQ BD, PQ EG = AE = 4 cm A B CD H E F G 4 cm P Q
- 27. Jarak garis kebidang Gambar disamping, menunjukan Jarak antara garis g ke bidang V adalah panjang ruas garis yang menghubungkan tegak lurus garis dan bidang g
- 28. Contoh Diketahui kubus ABCD.EFGH dengan panjang rusuk8 cm Jarak garis AE ke bidang BDHF adalah…. A B CD H E F G 8 cm P
- 29. Pembahasan Jarak garis AEke bidang BDHF diwakili oleh panjang AP.(AP AE AP BDHF) AP = ½ AC(AC BDHF) = ½.8√2 = 4√2 A B CD H E F G 8 cm P Jadi jarak A ke BDHF = 4√2 cm
- 30. V W Jarak Bidang danBidang peragaan, menunjukan jarak antara bidang W dengan bidang V adalah panjang ruas garis yang tegak lurus bidang W dan tegak lurus bidang V W
- 31. Contoh Diketahui kubus ABCD.EFGH dengan panjang rusuk6 cm. Jarak bidang AFH ke bidang BDG adalah…. A B CD H E F G 6 cm 6 cm
- 32. Pembahasan Jarak bidang AFH kebidang BDG diwakili oleh PQ PQ = ⅓ CE (CE diagonal ruang) PQ = ⅓. 9√3 = 3√3 A B CD H E F G 6 cm 6 cm P Q Jadi jarak AFH ke BDG = 4√2 cm
- 33. Sudut Pada BangunRuang: Sudut antara dua garis Sudut antara garis dan bidang Sudut antara bidang dan bidang
- 34. Sudut antara DuaGaris Yang dimaksud dengan besar sudut antara dua garis adalah besar sudut terkecil yang dibentuk oleh kedua garis tersebut k m
- 35. Contoh Diketahui kubus ABCD.EFGH Besar sudutantara garis-garis: a. AB dengan BG b. AH dengan AF c. BE dengan DF A B CD H E F G
- 36. Pembahasan Besar sudut antara garis-garis: a.AB dengan BG = 900 b. AH dengan AF = 600 (∆ AFH smss) c. BE dengan DF = 900 (BE DF) A B CD H E F G
- 37. P Q Sudut antara Garis danBidang Sudut antara garis a dan bidang dilambangkan (a, ) adalah sudut antara garis a dan proyeksinya pada . Sudut antara garis PQ dengan V = sudut antara PQ dengan P’Q = PQP’ P’
- 38. Contoh Pada limas segiempat beraturan T.ABCDyang semua rusuknya sama panjang, sudut antara TA dan bidang ABCD adalah…. T A B CD a cm a cm
- 39. Pembahasan • TA =TB = a cm • AC = a√2 (diagonal persegi) • ∆TAC = ∆ siku-siku samakaki T A B CD a cm a cm sudut antara TA dan bidang ABCD adalah sudut antara TA dan AC yang besarnya 450
- 40. Sudut antara Bidang danBidang Sudut antara bidang dan bidang adalah sudut antara garis g dan h, dimana g ( , ) dan h ( , ). ( , ) garis potong bidang dan ( , ) g h
- 41. Contoh Diketahui kubus ABCD.EFGH a. Gambarlahsudut antara bidang BDG dengan ABCD b. Tentukan nilai sinus sudut antara BDG dan ABCD! A B CD H E F G
- 42. Pembahasan a. (BDG,ABCD) • garispotong BDG dan ABCD BD • garis pada ABCD yang BD AC • garis pada BDG yang BD GP A B CD H E F G Jadi (BDG,ABCD) = (GP,PC) = GPC P
- 43. Pembahasan b. sin (BDG,ABCD) =sin GPC = = = ⅓√6A B CD H E F G Jadi, sin (BDG,ABCD) = ⅓√6 P GP GC x 6a a 2 1 .6 6 6 6 2 1