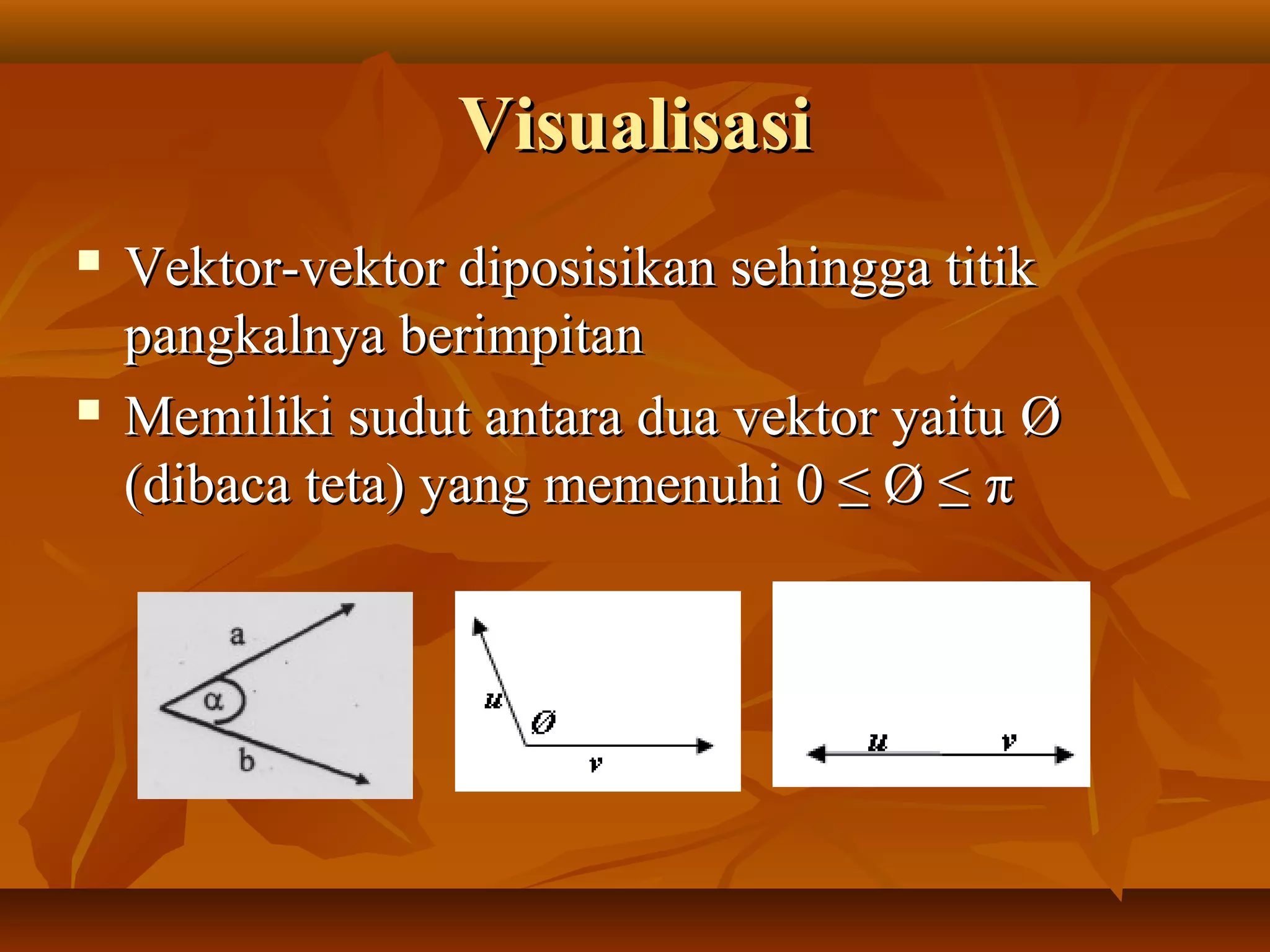
Dokumen ini membahas konsep aljabar vektor, termasuk perkalian vektor dengan skalar dan dot product, serta ruang vektor dan basisnya. Penjelasan mencakup sifat-sifat dasar, kombinasi linear, dan orthogonalitas vektor. Contoh soal disertakan untuk menjelaskan penerapan konsep-konsep tersebut dalam konteks geometri.

1. Aljabar LinearAljabar Linear
Pertemuan 2Pertemuan 2
Aljabar Vektor (Perkalian vektor)Aljabar Vektor (Perkalian vektor)
.:: Erna Sri Hartatik ::.

2. PembahasanPembahasan
 Perkalian vektor dengan skalarPerkalian vektor dengan skalar
 Ruang vektorRuang vektor
 Perkalian Vektor dengan Vektor:Perkalian Vektor dengan Vektor:
Dot ProductDot Product
- Model- Model dot productdot product
-- SifatSifat dot productdot product

3. PendahuluanPendahuluan
 Penambahan dan pengurangan vektor, merupakanPenambahan dan pengurangan vektor, merupakan
analisa sederhana dari aljabar vektoranalisa sederhana dari aljabar vektor
 Pada pembahasan ini akan dibahas bagaimana konsepPada pembahasan ini akan dibahas bagaimana konsep
perkalian vektor dalam ruang berdimensi 2 atauperkalian vektor dalam ruang berdimensi 2 atau
dimensi 3, serta penerapannya pada bidang geometri,dimensi 3, serta penerapannya pada bidang geometri,
khususnya dengan perkalian vektor dengan skalar dankhususnya dengan perkalian vektor dengan skalar dan
perkalianperkalian dot productdot product

4. PerkalianPerkalian
Vektor dengan SkalarVektor dengan Skalar

5. DefinisiDefinisi
 Untuk sembarang vektorUntuk sembarang vektor aa dengandengan αα, maka:, maka:
- panjang- panjang ααaa = |= | αα |.|a||.|a|
-- jikajika aa ≠ 0 dan≠ 0 dan αα > 0 ,> 0 , ααaa searah dengansearah dengan aa
-- jikajika aa ≠ 0 dan≠ 0 dan αα < 0 ,< 0 , ααaa berlawanan arah denganberlawanan arah dengan aa
-- jikajika aa = 0 dan= 0 dan αα = 0 , maka= 0 , maka ααaa = 0= 0
 Untuk vektorUntuk vektor aa dalam koordinat kartesiandalam koordinat kartesian
jikajika a =a = [a1,a2,a3] maka[a1,a2,a3] maka
ααa =a = [[ααaa1,1, ααaa22,, ααaa3]3]

6. Sifat Perkalian skalar ‘n vektorSifat Perkalian skalar ‘n vektor

7. Ruang VektorRuang Vektor
 Merupakan himpunan elemen vektor yangMerupakan himpunan elemen vektor yang
terdefinisikan sekurang-kurangnya dua operasi yangterdefinisikan sekurang-kurangnya dua operasi yang
membentuk groupmembentuk group
 Berlaku sifat distributif dan assosiatif gabunganBerlaku sifat distributif dan assosiatif gabungan
- distributif operasi 1 terhadap operasi 2- distributif operasi 1 terhadap operasi 2
- distributif operasi 2 terhadap operasi 1- distributif operasi 2 terhadap operasi 1
- assosiatif- assosiatif

8. Kombinasi linearKombinasi linear
 Untuk sembarang vektorUntuk sembarang vektor a1, … , ama1, … , am didalamdidalam
ruang vektorruang vektor vv , maka ungkapan:, maka ungkapan:
αα11aa1 +1 + αα22aa2 + … +2 + … + ααmm aam.m.
αα1, … ,1, … , ααm skalar sembarangm skalar sembarang
disebut sebagaidisebut sebagai “Kombinasi Linear”“Kombinasi Linear”

9. Ketergantungan LinearKetergantungan Linear
 Jika kombinasi linear dari m buah vektor sama dengan vektorJika kombinasi linear dari m buah vektor sama dengan vektor
nol dan berlaku hanya untuknol dan berlaku hanya untuk ααi = 0 (i=1,2,…,m), maka m buahi = 0 (i=1,2,…,m), maka m buah
vektor tersebut dikatakan sebagai ‘vektor-vektor bebas linear’vektor tersebut dikatakan sebagai ‘vektor-vektor bebas linear’
 Jika sekurang-kurangnya terdapat satuJika sekurang-kurangnya terdapat satu αα1=0, dimana1=0, dimana
kombinasi linear dari m buah vektor sama dengan vektor nol,kombinasi linear dari m buah vektor sama dengan vektor nol,
maka m buah vektor tersebut dikatakan sebagai ‘vektor-vektormaka m buah vektor tersebut dikatakan sebagai ‘vektor-vektor
bergantungan linear’bergantungan linear’
αα11aa1 +1 + αα22aa2 + … +2 + … + ααmm aam = 0m = 0
 Berlaku untukBerlaku untuk αα1 =1 = αα2 = … =2 = … = ααm = 0 (vektor2 bebas linear)m = 0 (vektor2 bebas linear)
terdapat minimal satuterdapat minimal satu αα1≠0 (vektor2 tidak bebas linear)1≠0 (vektor2 tidak bebas linear)

10. Basis ‘n Dimensi Ruang VektorBasis ‘n Dimensi Ruang Vektor
 Suatu vektor riilSuatu vektor riil RR memiliki dimensi n ditulis sebagaimemiliki dimensi n ditulis sebagai
RRn jika dan hanya jika terdapat n buah vektor dalamn jika dan hanya jika terdapat n buah vektor dalam
RR yang saling bebas linearyang saling bebas linear
 n buah vektor bebas linear dalamn buah vektor bebas linear dalam RR disebut sebagaidisebut sebagai
‘vektor basis’. Hal ini berarti setiap vektor lain dalam‘vektor basis’. Hal ini berarti setiap vektor lain dalam
RR selalu dapat dinyatakan sebagai kombinasi linearselalu dapat dinyatakan sebagai kombinasi linear
dari vektor-vektor basis.dari vektor-vektor basis.
 Vektor basis bmempunyai panjang 1 unitVektor basis bmempunyai panjang 1 unit

12. Perkalian TitikPerkalian Titik
(Dot Product)(Dot Product)

13. VisualisasiVisualisasi
 Vektor-vektor diposisikan sehingga titikVektor-vektor diposisikan sehingga titik
pangkalnya berimpitanpangkalnya berimpitan
 Memiliki sudut antara dua vektor yaituMemiliki sudut antara dua vektor yaitu ØØ
(dibaca teta) yang memenuhi 0 ≤ Ø ≤(dibaca teta) yang memenuhi 0 ≤ Ø ≤ ππ

14. RumusRumus
 JikaJika uu dandan vv adalah vektor-vektor dalam ruangadalah vektor-vektor dalam ruang
berdimensi-2 atau berdimensi-3 danberdimensi-2 atau berdimensi-3 dan Ø adalahØ adalah
sudut antarasudut antara uu dandan v,v, maka hasil kali titikmaka hasil kali titik u.vu.v
adalah:adalah:
u.v = |u||v|u.v = |u||v| cos Ø jikacos Ø jika u ≠u ≠ 0 dan0 dan v ≠v ≠ 00
u.v = 0u.v = 0 jikajika u =u = 0 dan0 dan v =v = 00

15. Orthogonalitas dua vektorOrthogonalitas dua vektor
 Dua vektor tidak nol dikatakan orthogonal (salingDua vektor tidak nol dikatakan orthogonal (saling
tegak lurus) jika dan hanya jika hasil kali dalamnyategak lurus) jika dan hanya jika hasil kali dalamnya
adalah nol.adalah nol.
 Beberapa formulasi dari perkalian titik ini dapat kitaBeberapa formulasi dari perkalian titik ini dapat kita
turunkan sebagai berikut:turunkan sebagai berikut:
bbaa
ba
ba
ba
aaaaaaaa
..
.
||||
.
cos
.||||0cos||||. 2
==
=⇒== °
α

16. SifatSifat Dot ProductDot Product
 Untuk setiap vektor sebarang a, b, c dan skalarUntuk setiap vektor sebarang a, b, c dan skalar
α1, α2 berlaku:α1, α2 berlaku:

17. Formulasi KhususFormulasi Khusus
Jika a da b dinyatakan dalam komponennya,Jika a da b dinyatakan dalam komponennya,
maka:maka:
a.b = a1 b1 + a2 b2 + a3 b3 ( vektor 3 dimensi )a.b = a1 b1 + a2 b2 + a3 b3 ( vektor 3 dimensi )
GenjangJajaranPersbababa
segitigamaanPertidaksababa
SchwarzmaanPertidaksababa
.)|||(|2||||
||||||
|||||.|
2222
⇒+=−++
⇒+≤+
⇒≤

18. Contoh SoalContoh Soal
Jika diketahui vektor a = [1,2,0], b=[3,-2,1].Jika diketahui vektor a = [1,2,0], b=[3,-2,1].
Tentukanlah:Tentukanlah:
- panjang vektor a, panjang vektor b, sudut antara vektor a dan b,panjang vektor a, panjang vektor b, sudut antara vektor a dan b,
- sudut vektor c = a + b terhadap sumbu –xsudut vektor c = a + b terhadap sumbu –x
Jawaban:Jawaban:

19. Contoh soal 2 :Contoh soal 2 :
Suatu partikel P dikenakan gaya tetap a yang menyebabkanSuatu partikel P dikenakan gaya tetap a yang menyebabkan
partikel tersebut bergerak sejauh d membentuk sudut αpartikel tersebut bergerak sejauh d membentuk sudut α
arah gaya a, maka kerja yang dilakukan oleh gayaarah gaya a, maka kerja yang dilakukan oleh gaya
tersebut adalah ?tersebut adalah ?
Jawab :Jawab :

20. Cara lain menyatakan dot producCara lain menyatakan dot produc
a.ba.b dituliskan pula sebagaidituliskan pula sebagai (a,b) : Inner Product(a,b) : Inner Product
|a| dituliskan pula sebagai|a| dituliskan pula sebagai ),(|||| baa =

21. SummarySummary
 Perkalian vektor dengan skalar merupakan perbesaranPerkalian vektor dengan skalar merupakan perbesaran
atau pengecilan vektor, dengan bilangan skalaratau pengecilan vektor, dengan bilangan skalar
merupakan satuan pembandingnya.merupakan satuan pembandingnya.
 vektor dalam ruangvektor dalam ruang RRn dapat dinyatakan sebagain dapat dinyatakan sebagai
kombinasi linear dari vektor-vektor basiskombinasi linear dari vektor-vektor basis
 Rumus untuk dot productRumus untuk dot product
 Perkalian titik (dot product) antara 2 vektor akanPerkalian titik (dot product) antara 2 vektor akan
menghasilkan suatu nilai skalarmenghasilkan suatu nilai skalar
u.v = |u||v|u.v = |u||v| cos Øcos Ø jikajika u ≠u ≠ 0 dan0 dan v ≠v ≠ 00
u.v = 0u.v = 0 jikajika u =u = 0 dan0 dan v =v = 00

22. Daftar PustakaDaftar Pustaka
Anton, Howard. Dasar-dasar Aljabar Linear Jilid 1 EdisiAnton, Howard. Dasar-dasar Aljabar Linear Jilid 1 Edisi
7. 2000. Penerbit Interaksara. Jakarta7. 2000. Penerbit Interaksara. Jakarta
Noor Ifada. Bahan Kuliah Aljabar LinearNoor Ifada. Bahan Kuliah Aljabar Linear
Anton, Howard. Dasar-dasar Aljabar Linear Jilid 2 EdisiAnton, Howard. Dasar-dasar Aljabar Linear Jilid 2 Edisi
7. 2000. Penerbit Interaksara. Jakarta7. 2000. Penerbit Interaksara. Jakarta