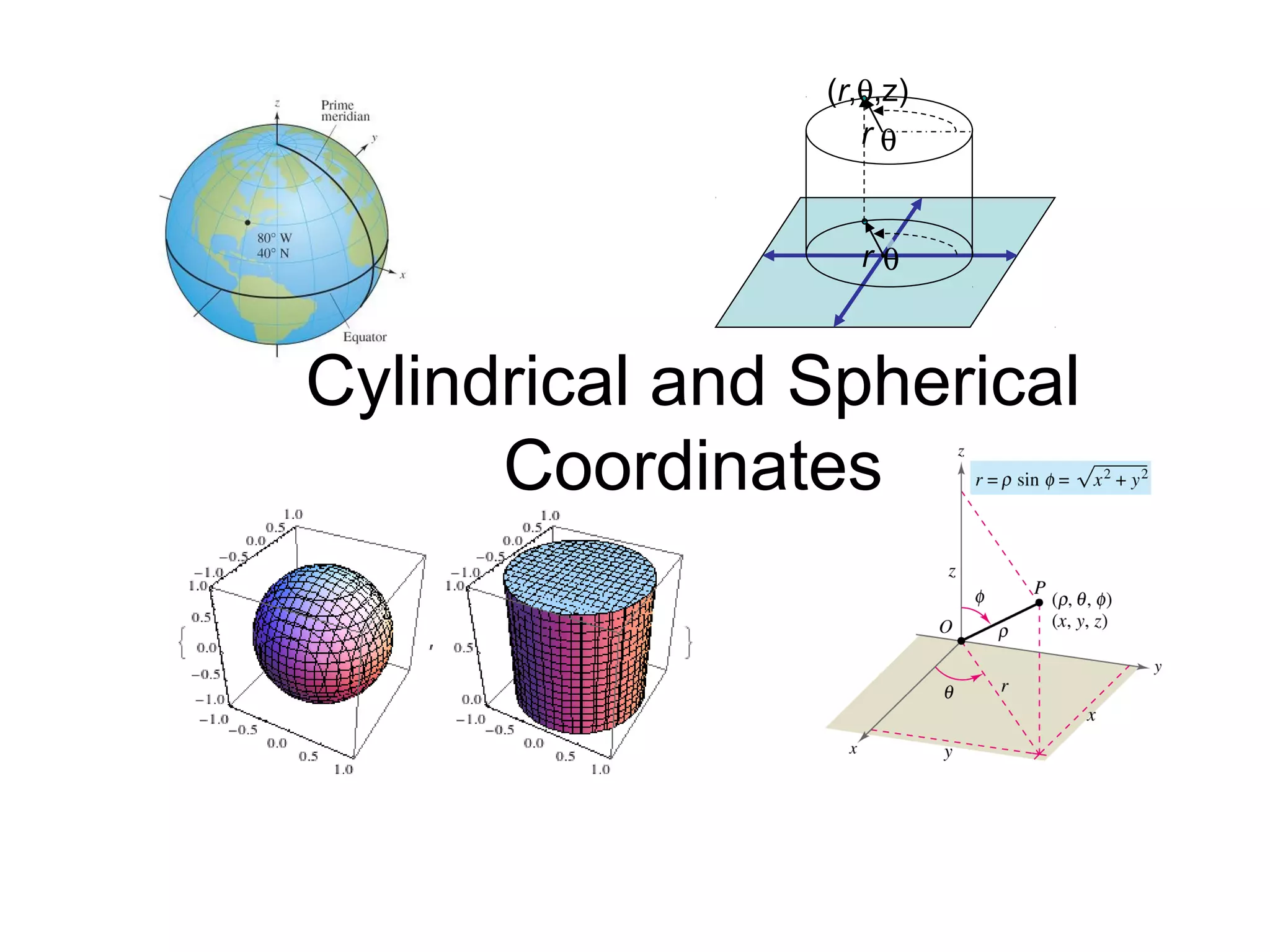
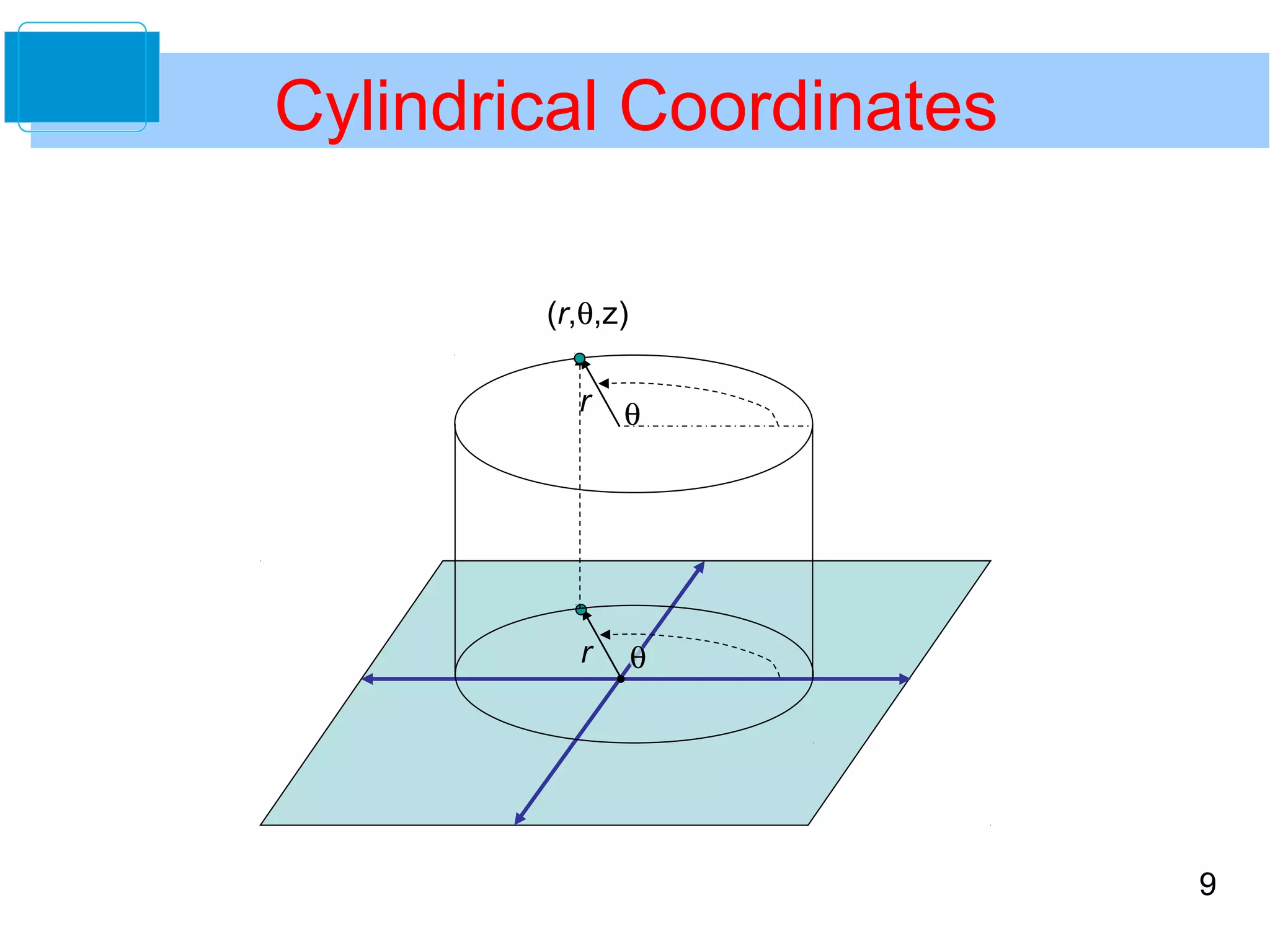
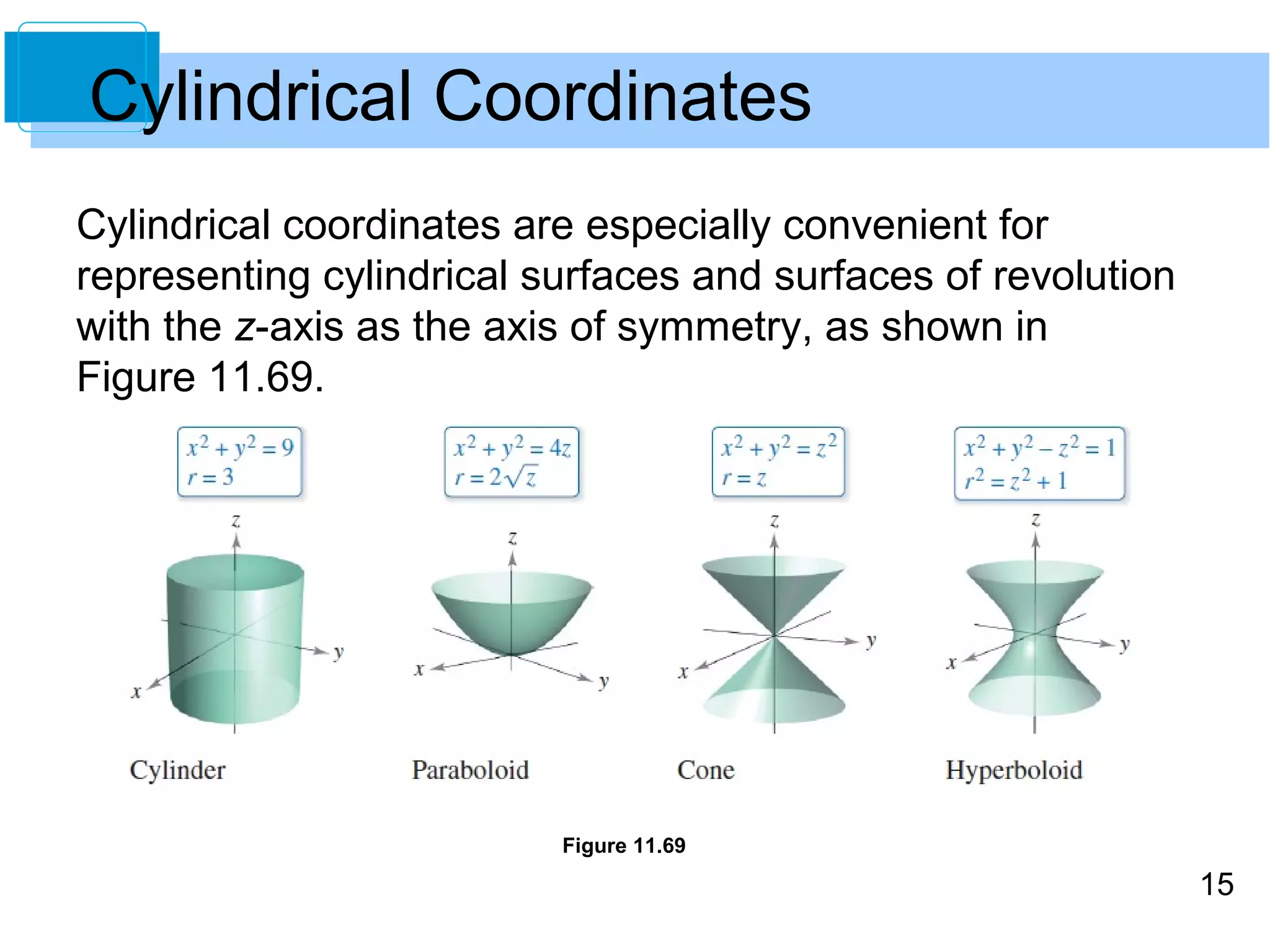
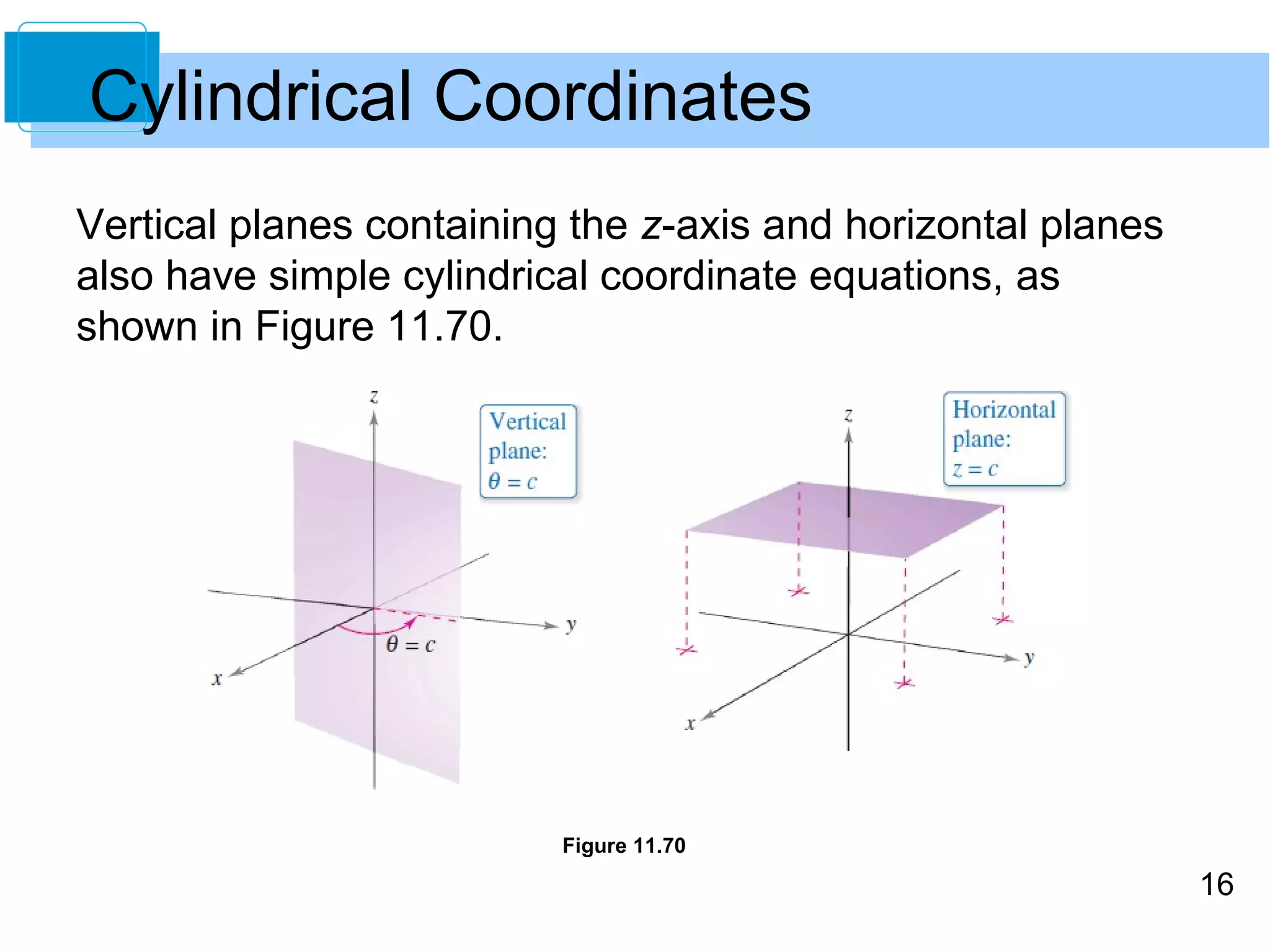
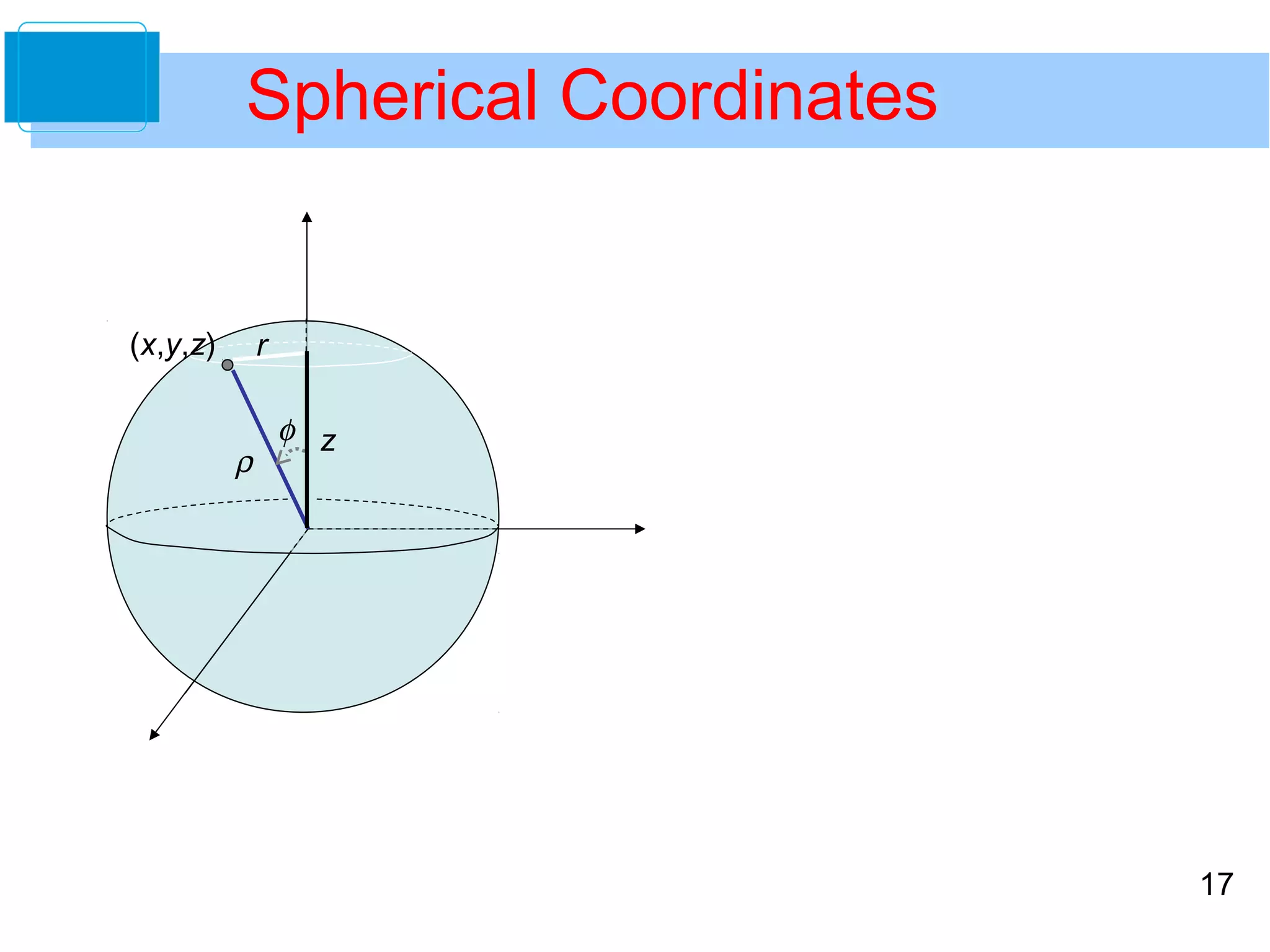
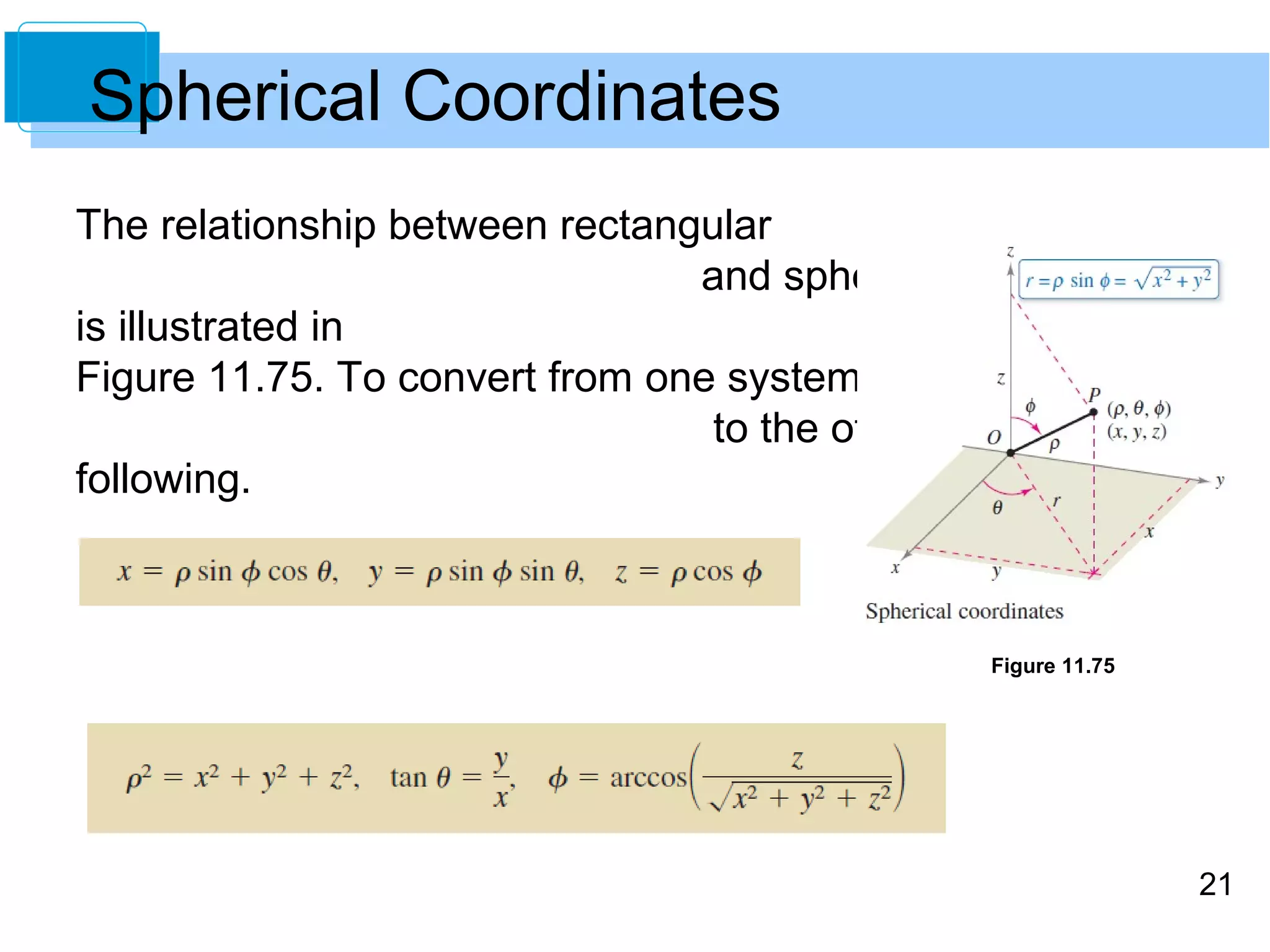
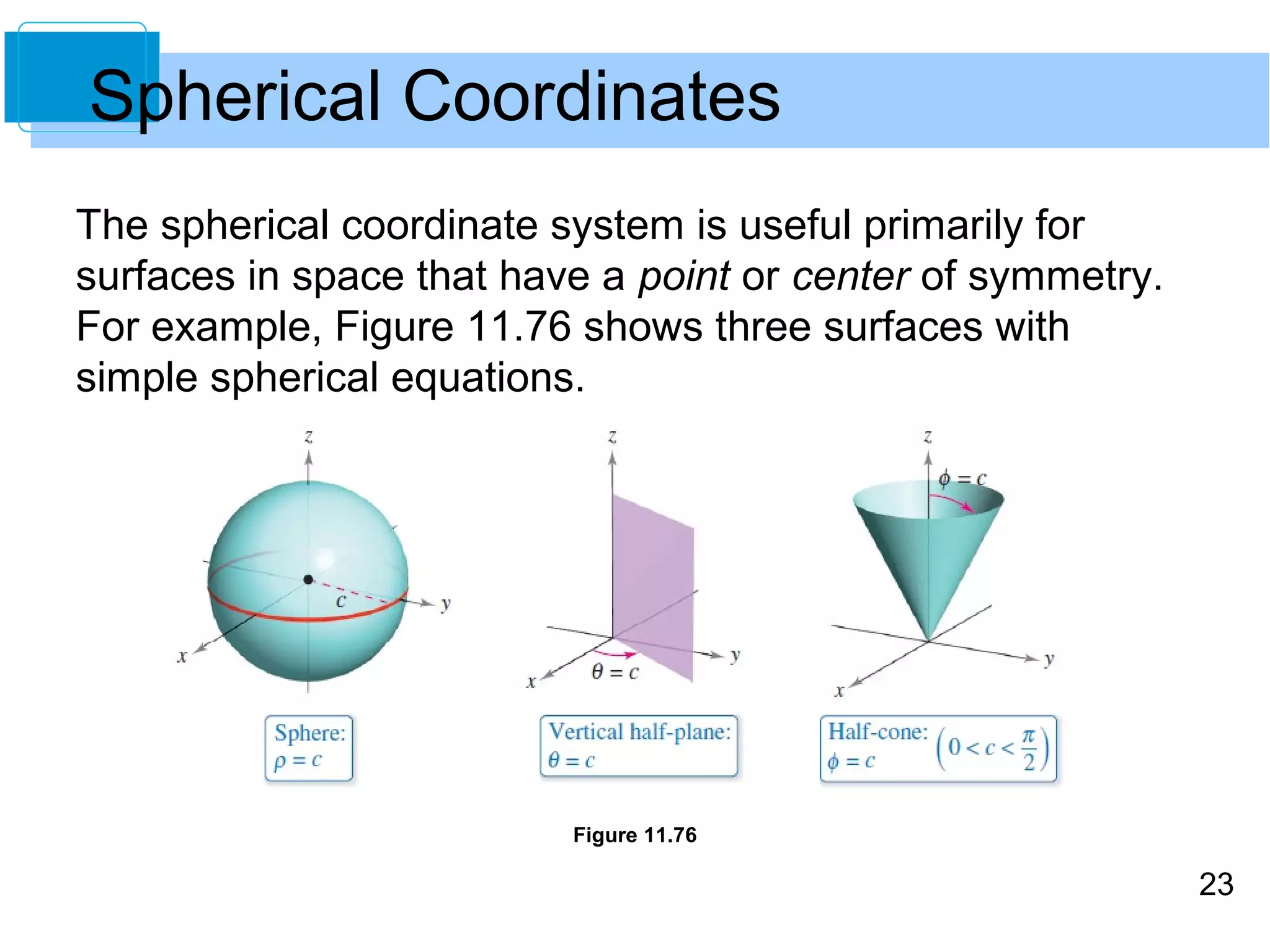
This document discusses cylindrical and spherical coordinate systems. It provides objectives for understanding these coordinate systems, converting between them and Cartesian coordinates, and developing problem-solving skills. Examples are given of converting between cylindrical and Cartesian coordinates, as well as spherical and Cartesian coordinates. Key aspects of cylindrical coordinates include representing points as (r,θ,z) and using conversion equations. Spherical coordinates represent points as (ρ,φ,θ) similar to latitude and longitude. Conversion equations are also provided between the cylindrical and spherical systems.

1. Cylindrical and Spherical
Coordinates
θr
θr
(r,θ,z)

2. 2
 Discuss the cylindrical and spherical coordinates;
 Solve the cylindrical and spherical coordinates in
Cartesian coordinates and vice versa;
 Develop patience and teamwork with their partners in
answering different problems of cylindrical and spherical
coordinates.
Objectives

3. 3

4. 4

5. 5

6. 6

7. 7

8. 8

9. 9
Cylindrical Coordinates
θr
θr
(r,θ,z)

10. 10
The cylindrical coordinate system is an extension of
polar coordinates in the plane to three-dimensional space.
Cylindrical Coordinates

11. 11
To convert from rectangular to cylindrical coordinates (or
vice versa), use the following conversion guidelines for
polar coordinates, as illustrated in Figure 11.66.
Figure 11.66
Cylindrical Coordinates

12. 12
Cylindrical to rectangular:
Rectangular to cylindrical:
The point (0, 0, 0) is called the pole. Moreover, because
the representation of a point in the polar coordinate system
is not unique, it follows that the representation in the
cylindrical coordinate system is also not unique.
Cylindrical Coordinates

13. 13
Convert the point (r, θ, z) = to rectangular
coordinates.
Solution:
Using the cylindrical-to-rectangular
conversion equations produces
So, in rectangular coordinates, the point
is (x, y, z) = as shown in Figure 11.67.
Example – Converting from Cylindrical to Rectangular Coordinates
Figure 11.67

14. 14
Example: Find the cylindrical coordinates of the point
(1,2,3) in Cartesian Coordinates

15. 15
Cylindrical Coordinates
Cylindrical coordinates are especially convenient for
representing cylindrical surfaces and surfaces of revolution
with the z-axis as the axis of symmetry, as shown in
Figure 11.69.
Figure 11.69

16. 16
Cylindrical Coordinates
Vertical planes containing the z-axis and horizontal planes
also have simple cylindrical coordinate equations, as
shown in Figure 11.70.
Figure 11.70

17. 17
Spherical Coordinates
φ
(x,y,z)
z
ρ
r

18. 18
Spherical Coordinates
In the spherical coordinate system, each point is
represented by an ordered triple: the first coordinate is a
distance, and the second and third coordinates are angles.
This system is similar to the latitude-longitude system used
to identify points on the surface of Earth.

19. 19
For example, the point on the
surface of Earth whose latitude
is 40°North (of the equator)
and whose
longitude is 80° West
(of the prime meridian) is shown
in Figure 11.74. Assuming that
the Earth is
spherical and has a
radius of 4000 miles, you would
label this point as
Figure 11.74
Spherical Coordinates

20. 20
Spherical Coordinates

21. 21
The relationship between rectangular
and spherical coordinates
is illustrated in
Figure 11.75. To convert from one system
to the other, use the
following.
Spherical to rectangular:
Rectangular to spherical:
Figure 11.75
Spherical Coordinates

22. 22
To change coordinates between the cylindrical and
spherical systems, use the following.
Spherical to cylindrical (r ≥ 0):
Cylindrical to spherical (r ≥ 0):
Spherical Coordinates

23. 23
The spherical coordinate system is useful primarily for
surfaces in space that have a point or center of symmetry.
For example, Figure 11.76 shows three surfaces with
simple spherical equations.
Figure 11.76
Spherical Coordinates

24. 24
Example – Convert (4,π/3,π/6) from spherical to
Cartesian coordinates.
Solution: From the given point (4,π/3,π/6), we get ρ = 4,
φ= π/3,and θ = π/6. We obtain the Cartesian coordinates
(x,y,z) as follows:
x = ρsinφcos θ x = 4sinπ/3cos π/6 x = 4(.87)(.87) = 3
y = ρsinφsinθ x = 4sinπ/3sin π/6 x = 4(.86)(0.5) = √3
z = ρcos θ z = 4cosπ/3 z = 4(0.5) = 2
Thus, the Cartesian coordinates of (4,π/3,π/6) is (3, √3, 2).

25. 25
Example – Rectangular-to-Spherical Conversion
Find an equation in spherical coordinates for the surface
represented by each rectangular equation.
a. Cone: x2
+ y2
+ z2
b. Sphere: x2
+ y2
+ z2
– 4z = 0
Solution:
Use the spherical-to-rectangular equations
and substitute in the rectangular equation as follows.

26. 26
So, you can conclude that
The equation Φ = π/4 represents the upper half-cone, and
the equation Φ = 3π/4 represents the lower half-cone.
Example – Solution cont’d

27. 27
Example 5 – Solution
b. Because and the
rectangular equation has the following spherical form.
Temporarily discarding the possibility that ρ = 0, you have
the spherical equation
cont’d

28. 28
Example 5 – Solution
Note that the solution set for this equation includes a point
for which ρ = 0, so nothing is lost by discarding the factor ρ.
The sphere represented by the equation ρ = 4cos Φ
is shown in Figure 11.77.
Figure 11.77
cont’d