Uploaded bySR Physics Academy
Gradient, Divergence and Curl of function
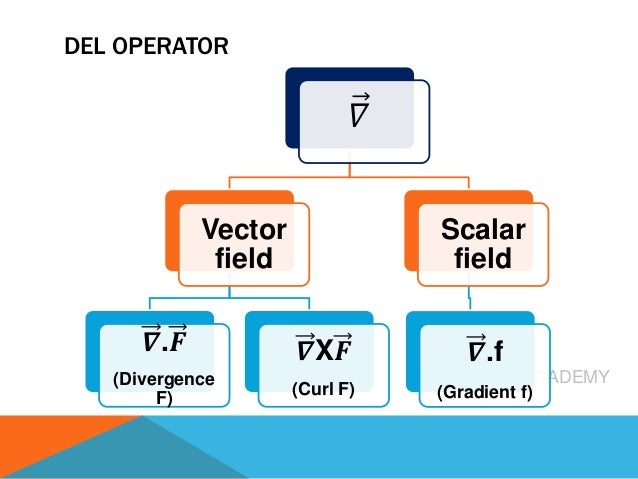
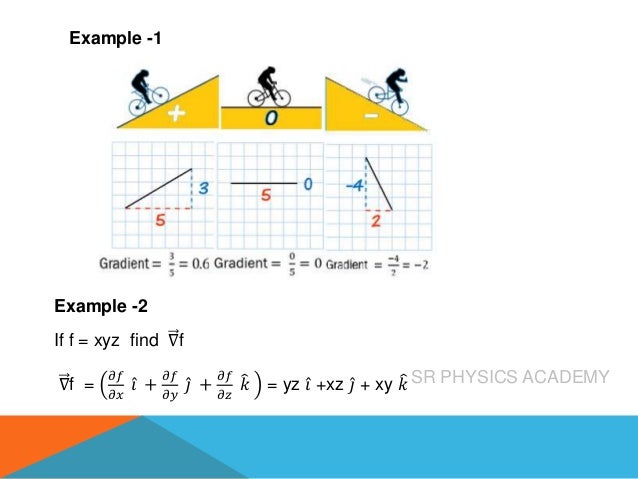
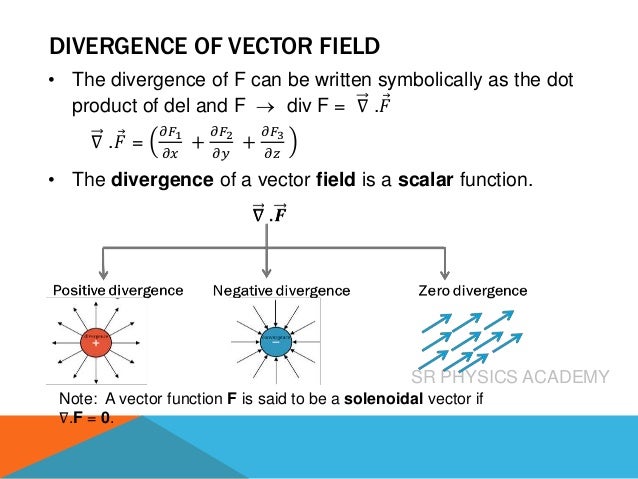
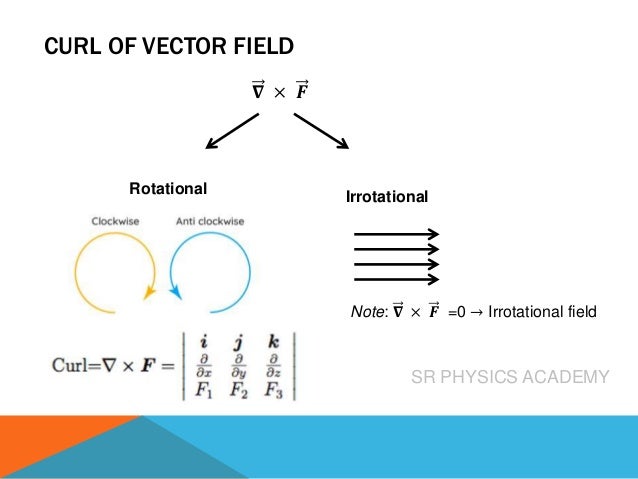
The del operator, also known as nabla (∇), is a collection of partial derivative operators used for scalar and vector fields in physics. It facilitates the computation of gradients, divergences, and curls, with specific outcomes for each; gradients yield vector quantities from scalars, divergences result in scalars from vectors, and curls produce vector quantities from vectors. The document includes examples and references a video for further learning about these concepts.
More Related Content
Similar to Gradient, Divergence and Curl of function
Gradient, Divergence and Curl of function
- 2. SR PHYSICS ACADEMY DELOPERATOR • The collection of partial derivate operators = 𝝏 𝝏𝒙 𝒊 + 𝝏 𝝏𝒚 𝒋 + 𝝏 𝝏𝒛 𝒌 is commonly called the del operator. • Its another name is `nabla‘. The symbol of nabla is represented by inverted triangle(∇). • There are three types of derivatives associated with the del operator. A scalar quantity has only magnitude. example- length, distance, volume, speed, time, temperature, work. A vector quantity has both magnitude and direction. example – velocity, force, displacement, momentum, acceleration.
- 3. SR PHYSICS ACADEMY DELOPERATOR 𝛻 Vector field 𝜵.𝑭 (Divergence F) 𝜵X𝑭 (Curl F) Scalar field 𝜵.f (Gradient f)
- 4. SR PHYSICS ACADEMY THEDEL OPERATOR Gradient of a scalar function is vector quantity. ∇ f Divergence of a vector function is scalar quantity. ∇ . 𝐅 Curl of a vector is a vector quantity. ∇ x 𝐅 ∇ = 𝝏 𝝏𝒙 𝒊 + 𝝏 𝝏𝒚 𝒋 + 𝝏 𝝏𝒛 𝒌
- 5. SR PHYSICS ACADEMY GRADIENTOF SCALAR FIELD • An operator which is always applied to a scalar field and resultant is a vector field. F(scalar field) → ∇f • If f is a function of three variables, the gradient vector is ∇f = 𝜕𝑓 𝜕𝑥 𝑖 + 𝜕𝑓 𝜕𝑦 𝑗 + 𝜕𝑓 𝜕𝑧 𝑘 • A gradient gives the rate of change of f( x , y , z) in any direction in space. Example - 𝐸 = −𝑔𝑟𝑎𝑑 𝑉 • Gradient of scalar field at any point gives the magnitude and direction of the maximum rate of change of the field. G = 𝑅𝑖𝑠𝑒 𝑅𝑢𝑛
- 6. SR PHYSICS ACADEMY Example-2 If f = xyz find ∇f ∇f = 𝜕𝑓 𝜕𝑥 𝑖 + 𝜕𝑓 𝜕𝑦 𝑗 + 𝜕𝑓 𝜕𝑧 𝑘 = yz 𝑖 +xz 𝑗 + xy 𝑘 Example -1
- 7. SR PHYSICS ACADEMY DIVERGENCEOF VECTOR FIELD • The divergence of F can be written symbolically as the dot product of del and F div F = ∇ .𝐹 ∇ .𝐹 = 𝜕𝐹1 𝜕𝑥 + 𝜕𝐹2 𝜕𝑦 + 𝜕𝐹3 𝜕𝑧 • The divergence of a vector field is a scalar function. Note: A vector function F is said to be a solenoidal vector if ∇.F = 0.
- 8. SR PHYSICS ACADEMY EXAMPLE IfF ( X, Y, Z) = XZ i + XYZ J − 𝒀𝟐K find div F. Solution: div F = ∇ .𝐹 ∇ .𝐹 = 𝝏 𝝏𝒙 𝒊 + 𝝏 𝝏𝒚 𝒋 + 𝝏 𝝏𝒛 𝒌 . XZ i + XYZ J
- 9. SR PHYSICS ACADEMY CURLOF VECTOR FIELD 𝛁 × 𝑭 Rotational Irrotational Note: 𝛁 × 𝑭 =0 → Irrotational field
- 10. SR PHYSICS ACADEMY Example:Find the curl of a vector field
- 11. Visit our YouTubeChannel SR Physics Academy and watch the video on Gradient, Divergence and Curl of a Function. Click the link to watch the video: https://youtu.be/LSZin_b3xmY Step 1: Search for ‘SR Physics Academy’ on YouTube. Step 2: Go to Playlist ’Electromagnetic theory in English’. Step 3: Watch the video ‘Gradient, Divergence and Curl of a Function’
- 12.