This document provides an overview of polar coordinates including:
- Polar coordinates use (r, Θ) notation where r is the distance from the origin and Θ is the angle from the polar axis.
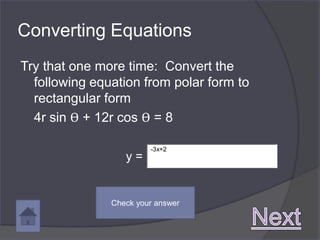
- Polar coordinates can be converted to rectangular coordinates using the equations x = r cos Θ and y = r sin Θ.
- Rectangular coordinates can be converted to polar coordinates by using the Pythagorean theorem to find r and trigonometric functions to find Θ.
- Examples are provided for converting between polar and rectangular coordinates.