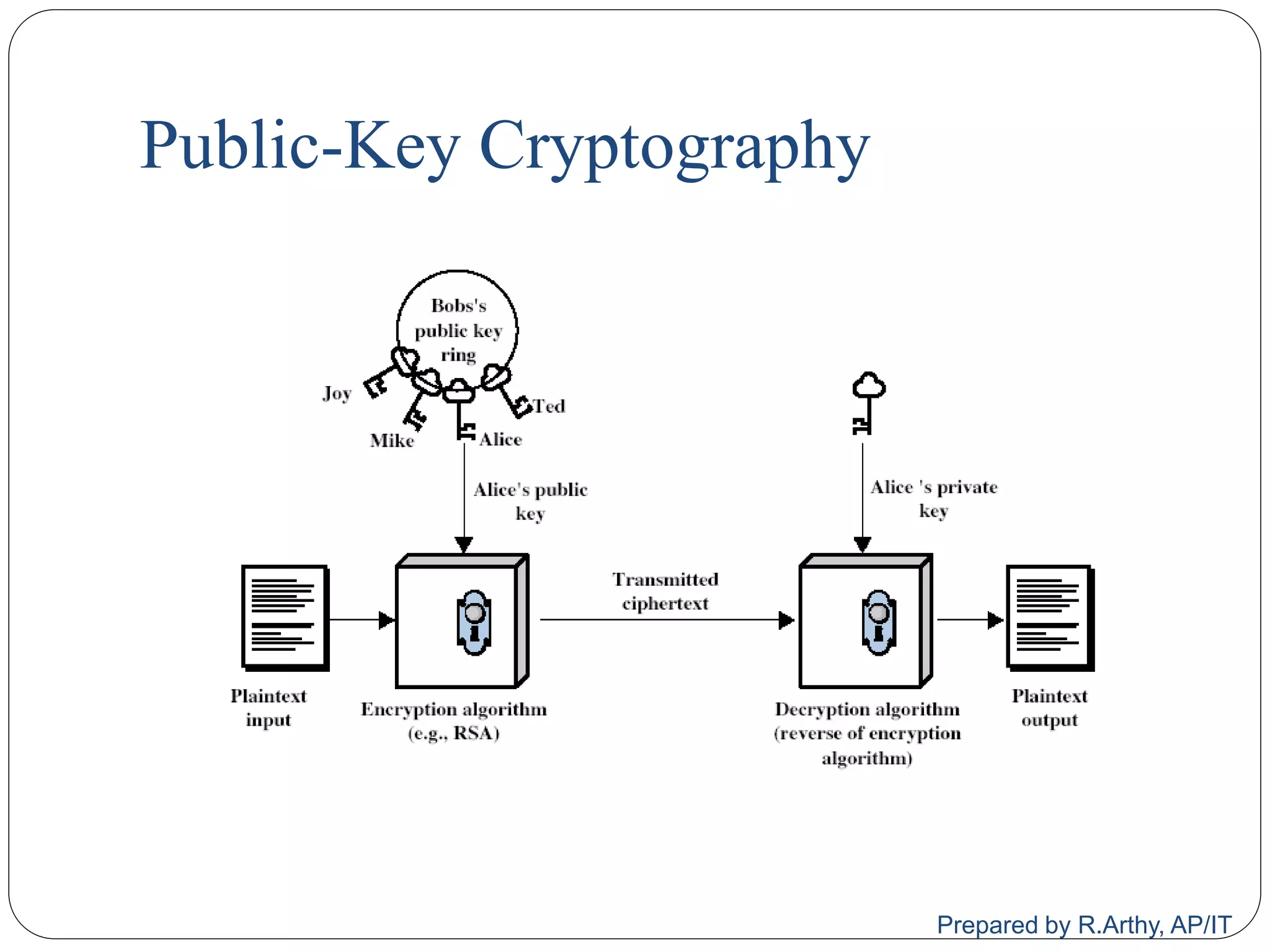
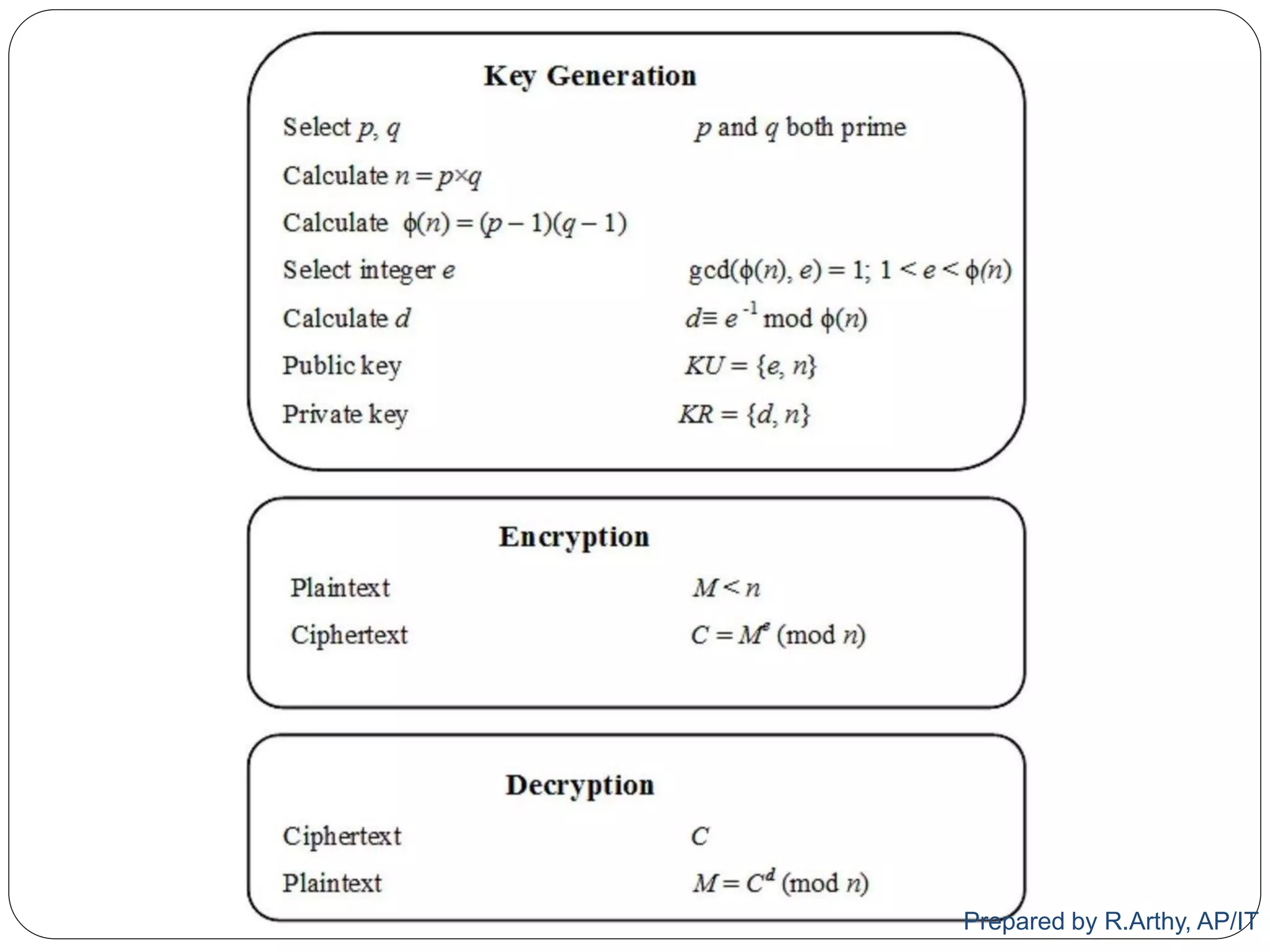
This document provides an overview of public key cryptography and asymmetric key ciphers. It begins with the underlying mathematics including primes, primality testing, factorization, Euler's totient function, Fermat's theorem, and exponentiation. It then discusses asymmetric key ciphers like RSA and Diffie-Hellman key exchange. RSA is described in more detail, including how public and private key pairs are generated using large prime numbers and exponentiation modulo a composite integer. Security relies on the difficulty of factoring large numbers.







![[contd…] Probabilistic Consideration
if Miller‐Rabin returns “composite” the number is
definitely not prime
otherwise is a prime or a pseudo‐prime
chance it detects a pseudo‐prime is < 1/4 chance it
detects a pseudo prime is < /4
hence if repeat test with different random a then
chance n is prime after t tests is:
Pr(n prime after t tests) = 1‐4‐t
eg. for t=10 this probability is > 0.99999
could then use the deterministic AKS test
Prepared by R.Arthy, AP/IT](https://image.slidesharecdn.com/cs8792-cns-unitiii-210730185219/75/Cs8792-cns-Public-key-cryptosystem-Unit-III-9-2048.jpg)







![[contd…]
Steps:
Find M = m1 * m2 * m3 *… *mk
Calculate
M1 = M/m1, M2 = M/m2, …, Mk = M/mk
Find the modulo inverse of Mi, i.e. M-1
1, M-1
2, …, M-1
k
Unique solution is
a = ((x1 * M1 * M-1
1) + (x2 * M2 * M-1
2) + … + (xk * Mk *
M-1
k)) mod M
Prepared by R.Arthy, AP/IT](https://image.slidesharecdn.com/cs8792-cns-unitiii-210730185219/75/Cs8792-cns-Public-key-cryptosystem-Unit-III-17-2048.jpg)


























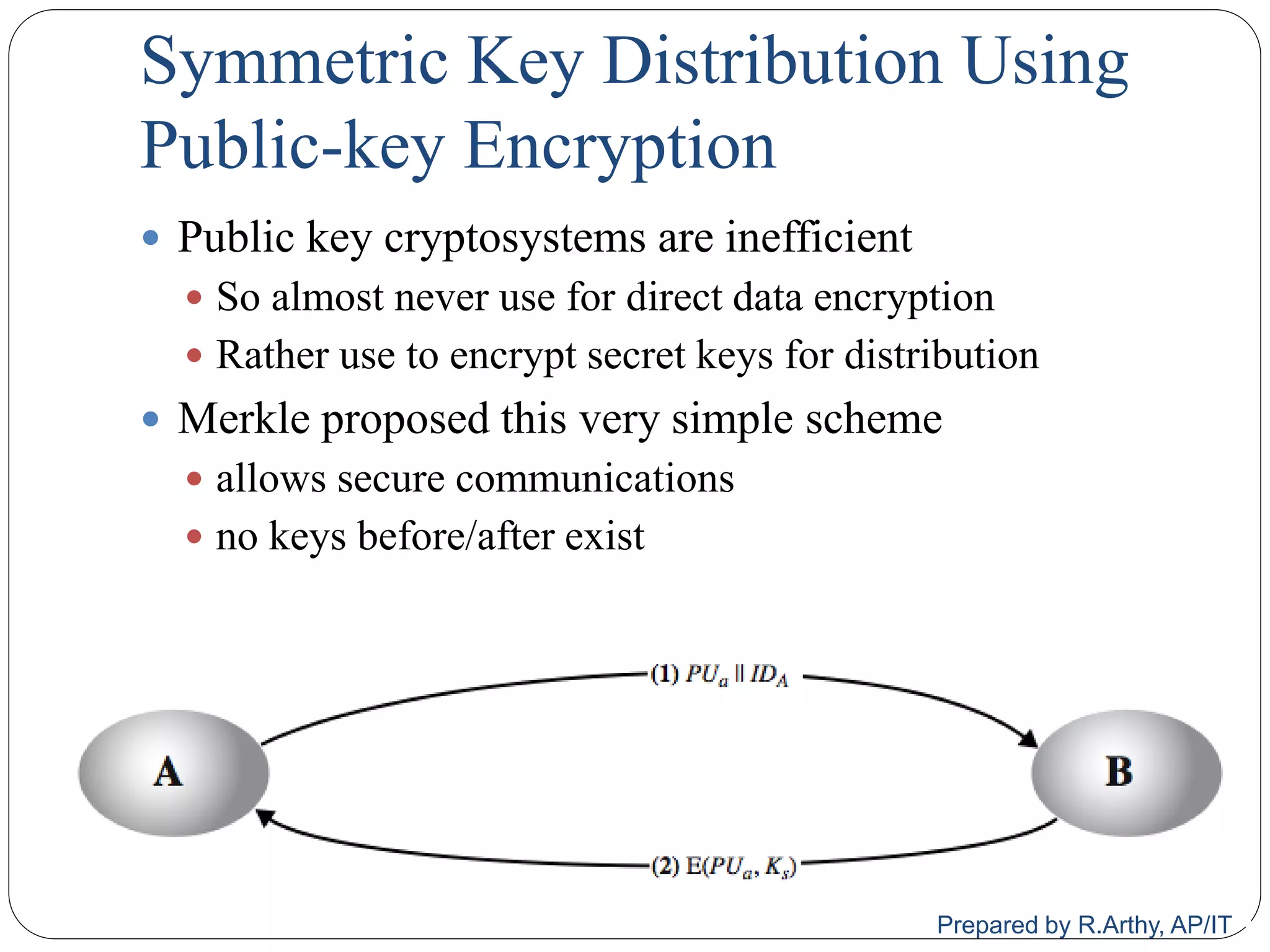
![[contd…]
Given parties A and B have various key distribution
alternatives:
A can select key and physically deliver to B
Third party can select & deliver key to A & B
If A & B have communicated previously can use
previous key to encrypt a new key
If A & B have secure communications with a third party
C, C can relay key between A & B
Prepared by R.Arthy, AP/IT](https://image.slidesharecdn.com/cs8792-cns-unitiii-210730185219/75/Cs8792-cns-Public-key-cryptosystem-Unit-III-46-2048.jpg)
![[contd…]
Key distribution using Key Distribution Center (KDC)
Prepared by R.Arthy, AP/IT](https://image.slidesharecdn.com/cs8792-cns-unitiii-210730185219/75/Cs8792-cns-Public-key-cryptosystem-Unit-III-47-2048.jpg)
![[contd…]
Hierarchies of KDC‟s required for large networks, but
must trust each other
Session key lifetimes should be limited for greater
security
Use of automatic key distribution on behalf of users,
but must trust system
Use of decentralized key distribution
Controlling key usage
Prepared by R.Arthy, AP/IT](https://image.slidesharecdn.com/cs8792-cns-unitiii-210730185219/75/Cs8792-cns-Public-key-cryptosystem-Unit-III-48-2048.jpg)
![[contd…]
Secret Key Distribution with Confidentiality and
Authentication
Prepared by R.Arthy, AP/IT](https://image.slidesharecdn.com/cs8792-cns-unitiii-210730185219/75/Cs8792-cns-Public-key-cryptosystem-Unit-III-50-2048.jpg)






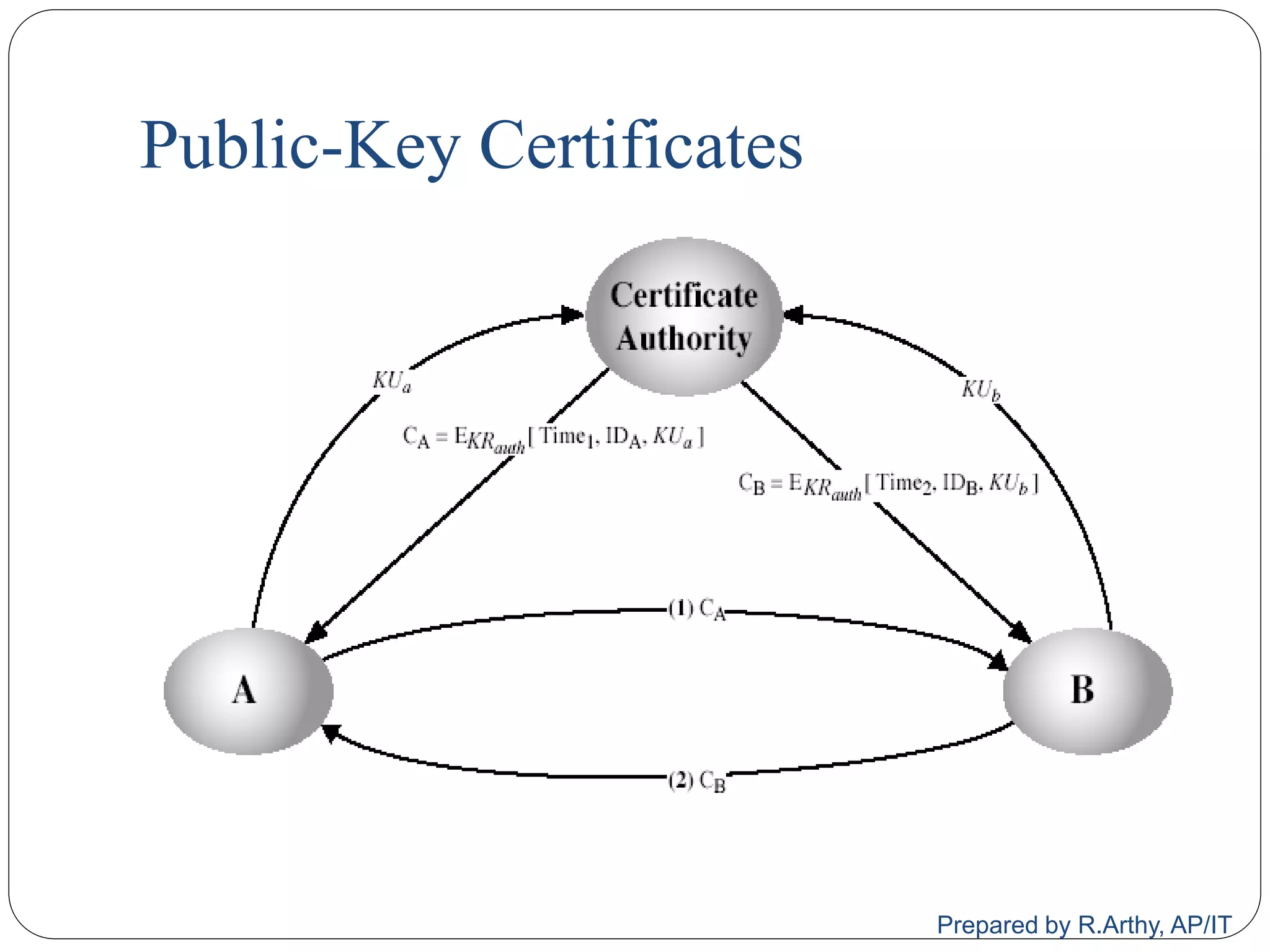



![[contd…]
A public-key distribution scheme
Cannot be used to exchange an arbitrary message
Rather it can establish a common key
Known only to the two participants
Value of key depends on the participants (and their
private and public key information)
Based on exponentiation in a finite (galois) field
(modulo a prime or a polynomial) - easy
Security relies on the difficulty of computing discrete
logarithms (similar to factoring) – hard
Prepared by R.Arthy, AP/IT](https://image.slidesharecdn.com/cs8792-cns-unitiii-210730185219/75/Cs8792-cns-Public-key-cryptosystem-Unit-III-61-2048.jpg)


![[contd…]
Prepared by R.Arthy, AP/IT](https://image.slidesharecdn.com/cs8792-cns-unitiii-210730185219/75/Cs8792-cns-Public-key-cryptosystem-Unit-III-64-2048.jpg)

















