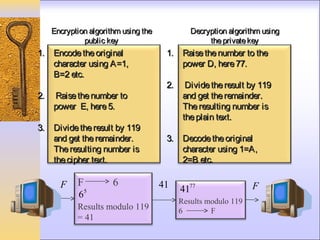
This document discusses Fermat's and Euler's theorems regarding prime numbers and their applications in cryptography. It begins by defining prime numbers, prime factorization, and greatest common divisors. It then explains Fermat's theorem that any integer to the power of a prime number minus one is congruent to one modulo that prime number. Next, it defines Euler's totient function and proves Euler's theorem, which generalizes Fermat's theorem. It concludes by providing an example of how these theorems can be applied to encrypt and decrypt messages in a public-key cryptography system.

1. Fermat and Euler’s
Theorems
Presented By :
Ankita Pandey
ME ECE- 112604

2. CONTENTS
 PRIME NUMBERS
 PRIME FACTORIZATION
 RELATIVELY PRIME NUMBERS
 GREATEST COMMON DIVISOR
 FERMAT’S THEOREM
 FERMAT THEOREM PROOF
 EULER TOTIENT FUNCTION
 EULER’S THEOREM
 APPLICATIONS
 SUMMARY
 REFERENCES

3. PRIME NUMBERS :

4. PRIME FACTORIZATION :

5. RELATIVELY PRIME NUMBERS :

6. GREATEST COMMON DIVISOR (GCD)

7. FERMAT’S THEOREM
≡
≡

8. FERMAT’S THEOREM PROOF :
 Consider a set of positive integers less than ‘p’ :
{1,2,3,…..,(p-1)} and multiply each element by ‘a’ and
‘modulo p’ , to get the set
X = {a mod p, 2a mod p,…, (p-1)a mod p}
 No elements of X is zero and equal, since p doesn’t
divide a.
 Multiplying the numbers in both sets (p and X) and
taking the result mod p yields

9. FERMAT’S THEOREM PROOF :
a * 2a *…* (p-1)a ≡ [1 * 2 * 3 *…* (p-1)] (mod p)
a p −1 ( p −1)! ≡ ( p −1)!(mod p )
Thus on equating (p-1)! term from both the sides,
since it is relatively prime to p, result becomes,
a p −1 ≡1(mod p )
An alternative form of Fermat’s Theorem is given as
a p ≡ a (mod p )

10. EULER TOTIENT FUNCTION : φ (n)
♦ φ (n) : How many numbers there are between
1 and n-1 that are relatively prime to n.
♦ φ (4) = 2 (1, 3 are relatively prime to 4).
♦ φ (5) = 4 (1, 2, 3, 4 are relatively prime to 5).
♦ φ (6) = 2 (1, 5 are relatively prime to 6).
♦ φ (7) = 6 (1, 2, 3, 4, 5, 6 are relatively prime
to 7).

11. EULER TOTIENT FUNCTION : φ (n)
♦ From φ (5) and φ (7), φ(n) will be n-1
whenever n is a prime number.
♦ This implies that φ (n) will be easy to
calculate when n has exactly two different
prime factors:
φ * Q) = (P-1)*(Q-1)
(P
if P and Q are prime.

12. EULER TOTIENT FUNCTION : φ (n)
♦ If GCD(a, p) = 1, and a < p, then
φ
≡a (p)
1(mod p).
♦ In other words, If a and p are relatively
prime, with a being the smaller integer, then
when we multiply a with itself φ (p) times and
divide the result by p, the remainder will be 1.

13. EULER’S THEOREM :
a Φ( n ) ≡ 1( mod n )

14. EULER’S THEOREM :
♦ Above equation is true if n is prime because
then,
Φ n ) = ( n −1)
(
and Fermat’s theorem holds.
♦ Consider the set of such integers, labeled as,
R = {x1 , x2 ,..., xΦ( n ) }
Here each element xi of R is unique positive
integer less than n with GCD( xi ,n ) = 1.

15. EULER’S THEOREM :
♦ Multiply each element by a, modulo n :
S = {( ax1 mod n ), ( ax2 mod n ),...., ( axΦ( n ) mod n )}
The set S is permutation of R :
 Because a and xi is relatively prime to n,
xi
so a must also be relatively prime to n.
Thus the elements of S are integers that
are less than n and that are relatively
prime to n.
 There are no duplicates in S.

16. EULER’S THEOREM :
♦ If axi mod n = ax j mod n then xi =x j
Φ )
(n Φ )
(n
∏(ax i mod n ) =∏xi
i=
1 i=
1
Φ )
(n Φ )
(n
∏ax
i=
1
i =∏(mod n )
xi
i=
1
 (n )
Φ
 Φn )
(
a Φ )
(n
× ∏≡
 xi ∏(mod n )
xi
i =
1  i= 1
a Φ n ) ≡ (mod n )
(
1

17. APPLICATIONS:

18. EXAMPLE :
1. Choose two large prime numbers P and Q.
Let P = 7 , Q = 17
2. Calculate N = P * Q.
Thus , N = 7 x 17 = 119
3. Select the public key (i.e. the encryption key) E such
that it is not a factor of (P-1)*(Q-1).
• Now (7-1) x (17-1) = 6 x 16 = 96.
• Factors of 96 are 2 and 3 (2 x 2 x 2 x 2 x 2 x 3).
• E has to be prime to 96, let E = 5.

19. EXAMPLE :
4. Select the private key (i.e. the decryption key) D such
that the following equation is true :
(D x E) mod (P-1) x (Q-1) = 1
• Substitute the values of E, P and Q in the equation
• Let choose D = 77 since
(5 x 77) mod 96 = 385 mod 96 = 1
Which satisfies the above condition.
5. For encryption, calculate the Cipher Text CT from the
Plain Text PT as follows :
CT = PTᴱ mod N.

20. EXAMPLE :
Let us consider of encoding of alphabets as A = 1,
B = 2, C = 3,….. , Z = 26.
We have to encrypt a single alphabet ‘ F’ (F = 6)
using this scheme, with B’ s public key as 77
(known to A and B) and B’ s private key as 5
(known only to B).
5
CT = PTᴱ mod 119 =6 mod 119 = 41
6. Send CT as the cipher text to the reciever.
Send 41 as the cipher text to the reciever.

21. EXAMPLE :
7. For decryption at the reciever, calculate the plain text
PT from the cipher text CT as follows :
PT = CTᴰ mod N.
PT = CTᴰ mod 119 =
77
41 mod 119 = 6
Which was the original plain text i.e. the code of
‘F’.

22. Encryption algorithm using the Decryption algorithm using
public key the private key
1. Encode the original 1. Raise the number to the
character using A=1, power D, here 77.
B=2 etc.
2. Divide the result by 119
2. Raise the number to and get the remainder.
power E, here 5. The resulting number is
the plain text.
3. Divide the result by 119
and get the remainder. 3. Decode the original
The resulting number is character using 1=A,
the cipher text. 2=B etc.
F F 6 41 F
5 4177
6
Results modulo 119
Results modulo 119 6 F
= 41

23. SUMMARY :
 Firstly Prime Numbers, Prime Factorization
And Greatest Common Divisor were
discussed.
 Secondly Fermat’s Theorem and its proof is
done.
 Then Euler Totient Function is discussed.
 Lastly Euler’s Theorem is discussed.

24. REFERENCES :
[1] Cryptography and Network Security Principles
and Practice, Fifth Edition, By: William Stallings.
[2] Cryptography and Network Security, Chapter 9
Mathematics of Cryptography, Part III: Primes and
Related Congruence Equations, By: Behrouz
Forouzan.
[3]L. Levine, Fermat's Little Theorem: A Proof by
Function Iteration," Math. Mag. 72 (1999), 308-
309.
[4] C. Smyth, A Coloring Proof of a Generalisation
of Fermat's Little Theorem," Amer. Math. Monthly
93 (1986), 469-471.

25. THANK YOU.