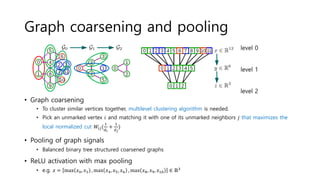
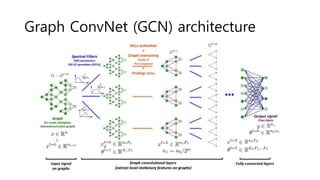
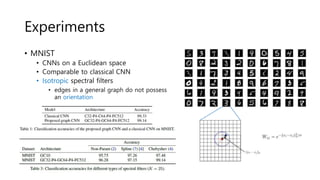
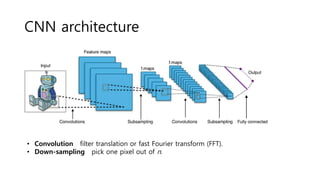
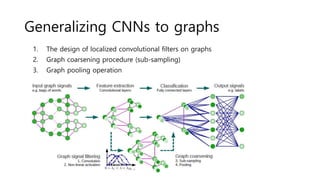
The document discusses the application of convolutional neural networks (CNNs) on graphs, particularly for unstructured data such as social, biological, and infrastructure networks. It highlights methods for formulating convolution and down-sampling on graphs, including the design of localized convolutional filters and graph coarsening techniques. The findings suggest that utilizing spectral graph theory can lead to efficient graph filtering and pooling, with proposed contributions towards linear complexity in filter design.

1. Convolutional Neural Networks on Graphs
with Fast Localized Spectral Filtering
Defferrard, Michaël, Xavier Bresson, and Pierre Vandergheynst
NIPS 2016

2. Unstructured data as graphs
• Majority of data is naturally unstructured, but can be
structured.
• Irregular / non-Euclidean data can be structured with graphs
• Social networks: Facebook, Twitter.
• Biological networks: genes, molecules, brain connectivity.
• Infrastructure networks: energy, transportation, Internet, telephony.
• Graphs can model heterogeneous pairwise relationships.
• Graphs can encode complex geometric structures.

3. CNN architecture
• Convolution filter translation or fast Fourier transform (FFT).
• Down-sampling pick one pixel out of n.

4. Generalizing CNNs to graphs
• Challenges
• Formulate convolution and down-sampling
on graphs
• How to define localized graph filters?
• Make them efficient

5. Generalizing CNNs to graphs
1. The design of localized convolutional filters on graphs
2. Graph coarsening procedure (sub-sampling)
3. Graph pooling operation

6. • 𝐺 = (𝑉, 𝐸, 𝑊) : undirected
and connected graph
• Spectral graph theory
• Graph Laplacians
• 𝐿 = 𝐷 − 𝑊
• Normalized Laplacians
𝐿 = 𝐼 𝑛 – 𝐷−
1
2 𝑊𝐷−
1
2
 𝑉 : set of vertices
 𝐸 : set of edges
 𝑊 : weighted adjacency matrix
 𝐷𝑖𝑖 = 𝑗 𝑊𝑖𝑗 : diagonal degree matrix
 𝐼 𝑛 : identity matrix
Graph Fourier Transform

7. Graph Fourier Transform
• Graph Fourier Transform
• 𝐿 = 𝑈Λ𝑈 𝑇 (Eigen value decomposition)
• Graph Fourier basis 𝑈 = [𝑢0, … , 𝑢 𝑛−1]
• Graph frequencies Λ =
𝜆0 ⋯ 0
⋮ ⋱ ⋮
0 ⋯ 𝜆 𝑛−1
1. Graph signal 𝑥 ∶ 𝑉 → ℝ, 𝑥 ∈ ℝ 𝑛
2. Transform 𝑥 = 𝑈 𝑇 𝑥 ∈ ℝ 𝑛

8. Spectral filtering of graph signals
• Convolution on graphs
• 𝑥 ∗ 𝒢 𝑦 = 𝑈 𝑈 𝑇 𝑥 ⊙ 𝑈 𝑇 𝑦
• filtered signal 𝑦 = 𝑔 𝜃 L x = 𝑔 𝜃 UΛ𝑈 𝑇
x = 𝑈𝑔 𝜃 Λ 𝑈 𝑇
𝑥
= 𝑈
𝑔 𝜃(𝜆0) ⋯ 0
⋮ ⋱ ⋮
0 ⋯ 𝑔 𝜃(𝜆 𝑛−1)
𝑈 𝑇 𝑥
• A non-parametric filter 𝑔 𝜃 Λ = diag 𝜃 , 𝜃 ∈ ℝ 𝑛
 Non-localized in vertex domain
 Learning complexity in O(n)
 Computational complexity in O(n2)

9. Polynomial parametrization for localized filters
• 𝑔 𝜃 Λ = diag 𝜃 , 𝜃 ∈ ℝ 𝑛
𝑔 𝜃 Λ = 𝑘=0
𝐾−1
𝜃 𝑘Λ 𝑘
, 𝜃 ∈ ℝ 𝑘
 𝐾 𝑡ℎ
order polynomials of the Laplacian -> 𝐾-localized
 Learning complexity in O(K)
 Still, computational complexity in O(n2
) because of multiplication with Fourier
basis U
• Filter localization on graph

10. Recursive formulation for fast filtering
• 𝑔 𝜃 Λ = 𝑘=0
𝐾−1
𝜃 𝑘Λ 𝑘 , 𝜃 ∈ ℝ 𝑘 𝑔 𝜃 Λ = 𝑘=0
𝐾−1
𝜃 𝑘Tk(Λ) , 𝜃 ∈ ℝ 𝑘
• Chebyshev expansion
𝑇𝑘(𝑥) = 2𝑥𝑇𝑘−1(𝑥) − 𝑇𝑘−2(𝑥)
• Filtered 𝑦 = 𝑔 𝜃 𝐿 𝑥
• 𝐾 multiplications by a sparse 𝐿
costs 𝑂 𝐾 𝐸 ≪ 𝑂(𝑛2)
 Learning complexity in 𝑂(𝐾)
 Computational complexity in 𝑂(𝐾|𝐸|)

11. Graph coarsening and pooling
• Graph coarsening
• To cluster similar vertices together, multilevel clustering algorithm is needed.
• Pick an unmarked vertex 𝑖 and matching it with one of its unmarked neighbors 𝑗 that maximizes the
local normalized cut 𝑊𝑖𝑗(
1
𝑑 𝑖
+
1
𝑑 𝑗
)
• Pooling of graph signals
• Balanced binary tree structured coarsened graphs
• ReLU activation with max pooling
• e.g. 𝑧 = max 𝑥0, 𝑥1 , max 𝑥4, 𝑥5, 𝑥6 , max 𝑥8, 𝑥9, 𝑥10 ∈ ℝ3
level 0
level 1
level 2

12. Graph ConvNet (GCN) architecture

13. Experiments
• MNIST
• CNNs on a Euclidean space
• Comparable to classical CNN
• Isotropic spectral filters
• edges in a general graph do not possess
an orientation

14. Experiments
• 20NEWS
• structure documents with a
feature graph
• 10,000 nodes, 132,834 edges
𝑂(𝑛2
)
𝑂(𝑛)

15. Conclusion
• Contributions
• Spectral formulation of CNNs on graphs in GSP
• Strictly localized spectral filters are proposed
• Linear complexity of filters
• Efficient pooling on graphs
• Limitation
• Filters are not directly transferrable to a different graph

16. References
• Deep Learning on Graphs, a lecture on A Network Tour of Data Science
(NTDS) 2016
• Shuman, David I., et al. "The emerging field of signal processing on
graphs: Extending high-dimensional data analysis to networks and other
irregular domains." IEEE Signal Processing Magazine 30.3 (2013): 83-98.
• How powerful are Graph Convolutions? (http://www.inference.vc/how-
powerful-are-graph-convolutions-review-of-kipf-welling-2016-2/)
• GRAPH CONVOLUTIONAL NETWORKS (http://tkipf.github.io/graph-
convolutional-networks/)