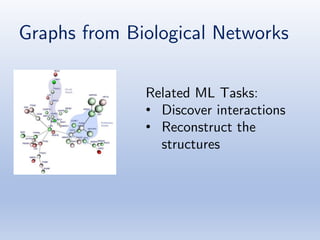
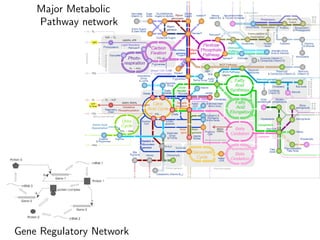
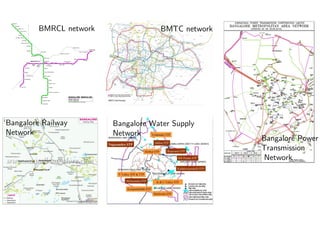
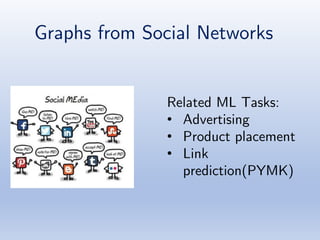
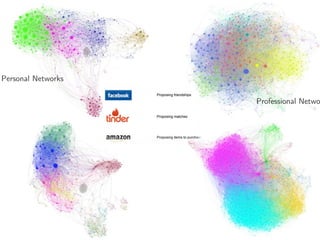
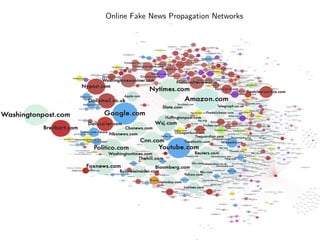
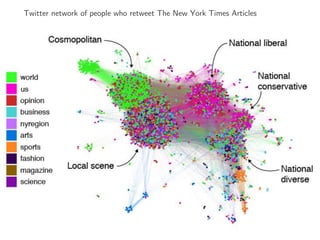
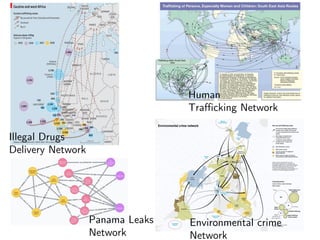
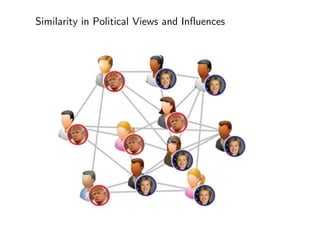
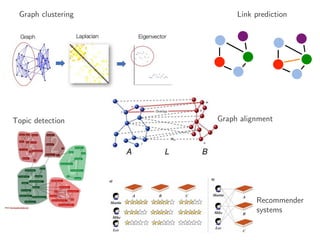
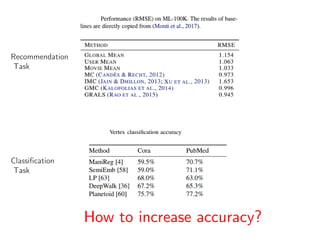
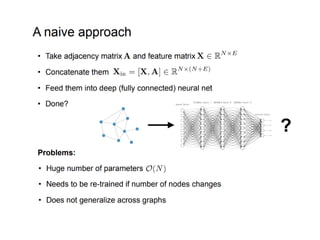
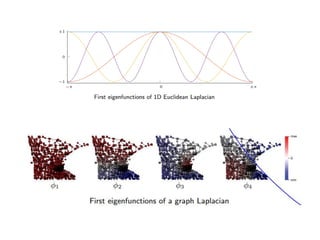
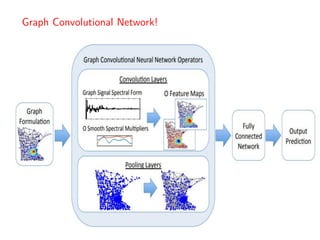
The document discusses deep learning applications on graphs, covering various types of networks including social, biological, and utility networks. It features an overview of graph-based machine learning techniques, such as spectral graph convolutions and applications of graph convolutional networks, including semi-supervised learning and distance metric learning. Recent developments in relational deep learning and multiple references for further exploration of the topic are also included.

1. Deep Learning on Graphs
Sushravya GM
16th June 2018
(@Deep Learning Bangalore Meetup)

2. Contents
1. Quick look at day-to-day graphs & related ML
applications
(social/biological/information/utility/similarity
networks)
2. Overview of graph-based Machine Learning
3. Search for better results with Deep Learning
4. Introduction to Spectral Graph Convolutions
5. Example Applications of Graph Convolutional
Networks
6. Recent Developments in Relational Deep Learning

3. Graphs from Biological Networks
Related ML Tasks:
• Discover interactions
• Reconstruct the
structures

4. Major Metabolic
Pathway network
Gene Regulatory Network

5. Functional Brain Networks

6. Graphs from Utility Networks
Related ML Tasks:
• Identify the node of
interest
• Best routing under
unknown costs

7. BMRCL network BMTC network
Bangalore Power
Transmission
Network
Bangalore Railway
Network
Bangalore Water Supply
Network

8. Graphs from Social Networks
Related ML Tasks:
• Advertising
• Product placement
• Link
prediction(PYMK)

9. Professional Netwo
Personal Networks

10. Graphs from Information Networks
Related ML Tasks:
• Identify influential
sources
• Search tasks (eg. Page
Rank)

11. Online Fake News Propagation Networks

12. Twitter network of people who retweet The New York Times Articles

14. Illegal Drugs
Delivery Network
Human
Trafficking Network
Panama Leaks
Network
Environmental crime
Network

16. Game of Thrones
Character Network
Star Wars
Character Network

17. Graphs from Similarity Networks
Related ML Tasks:
• Semi-supervised
learning
• Spectral clustering
• Manifold learning

19. Similarity in Philosophical Views and Influences

20. Similarity in Political Views and Influences

22. Overview of graph based
Machine Learning
▪ Graph clustering
▪ Topic detection
▪ Recommender systems
▪ Graph-based classification
▪ Link prediction
▪ Graph alignment
▪ Dynamic graphs
▪ Graph signal processing

23. Graph clustering
Topic detection
Link prediction
Graph alignment
Recommender
systems

24. Recommendation
Task
Classification
Task
How to increase accuracy?

26. Search for better results
with Deep Learning..

27. Image processing
Speech processing
Natural language
processing

28. How To Increase Accuracy?
Using Deep Learning to exploit:
1. Translation Invariance (weight sharing)
2. Hierarchical Compositionality
Take advantage of the structure of the data!!
But, in case of Graphs, where do we start?

29. Data from Regular domains
(Grids/Lattices)
Data from Irregular domains

30. Data from Regular domains Data from Irregular domains
?

31. We pick an assumption and work forwards!
Assumption:
Data from the graph domain are locally stationary and
manifest hierarchical structures
Next Challenge:
How to define compositionality
(convolution and pooling mechanisms) on graph data?

32. Convolutions on regular data
simple Spatial Filtering!

33. Extending the Concept of CNNs to Graph domain
Two possibilities…
1. Spatial Filtering: Sliding a filter of defined receptive
field(patch) across the graph.
2. Spectral Filtering: Exploiting the concept that
convolutions in spatial domain correspond to
multiplications in Fourier domain.

34. Spatial Filtering:
(+) Most Natural Analogy with the regular
structures. (intuitive)
(-) Requires defining a neighbourhood system and
a node ordering. (not at all intuitive)
Spatial Filtering:
(+) Does not require defining a neighbourhood
system and a node ordering. Can obtain strictly
localized filters.
(-) Extracted features non-transferable between
graphs

35. (from DSP) The convolution theorem states that In other words,
convolution of two functions in one domain equals point-wise
multiplication in the other domain.
For Image data,
Fourier
Transform
Multiplied
with a
Filter
in frequency
domain
Fourier
Transform Inverse
Fourier
Transform

36. What about graph data?
How to project the graph signals into the frequency domain?
Spatial domain (G) => Spectral
domain(G)
Steps:
1. Compute Graph Laplacian.
2. Decompose it into a full matrix of
orthonormal eigenvectors
But,
1. What is Graph Laplacian?
2. What are Eigen Vectors?
3. How to decompose Graph Laplacian into a matrix of orthonormal
eigenvectors?

37. What is Graph Laplacian?

38. What are Eigen Values and Eigen Vectors?
Eigenvalues are closely related to almost all major invariants
of a graph, linking one extremal property to another
The eigen values reflect the
importance of the corresponding
eigen vectors in reconstructing
the original graph structure.

39. How to decompose Graph Laplacian into a matrix of
orthonormal eigenvectors?

41. Convolution in regular domain
G is circular in structure. Hence, shift invariant!
Filter coefficients do not depend on basis.

42. Convolution in Irregular domain

43. Graph Convolutional Network!

44. Example Applications of Graph
Convolutional Networks
Application 1: Semi-supervised Node Classification
Application 2: Distance Metric Learning
Application 3: Geometric Matrix Completion

45. Application 1: Semi-supervised Node Classification

47. Application 2: Semi-supervised Node Classification

49. Application 3: Geometric Matrix Completion
Recurrent Multi-Graph Neural Networks

51. Recent Developments in
Relational Deep Learning
1. Relational inductive biases, deep learning,
and graph networks
2. Relational Deep Reinforcement Learning
3. Relational recurrent neural networks

56. References:
• Deep Feature Learning for Graphs
https://arxiv.org/pdf/1704.08829.pdf
• Learning Convolutional Neural Networks for Graphs
http://proceedings.mlr.press/v48/niepert16.pdf
• Deep Learning on Graphs with Graph Convolutional Networks [ppt]
http://deeploria.gforge.inria.fr/thomasTalk.pdf
• Graph Convolutional Networks [blog]
http://tkipf.github.io/graph-convolutional-networks/
• Geometric deep learning: going beyond Euclidean data
https://arxiv.org/pdf/1611.08097.pdf
• Convolutional Neural Networks on Graphs [ppt]
http://helper.ipam.ucla.edu/publications/dlt2018/dlt2018_14506.pdf
• CayleyNets: Graph Convolutional Neural Networks with Complex Rational Spectral Filters
https://arxiv.org/pdf/1705.07664.pdf

57. • Deep Geometric Matrix Completion [ppt]
http://helper.ipam.ucla.edu/publications/dlt2018/dlt2018_14552.pdf
• On Computational Hardness and Graph Neural Networks
http://helper.ipam.ucla.edu/publications/dlt2018/dlt2018_14508.pdf
• Machine Learning Meets Geometry [ppt]
http://geometry.cs.ucl.ac.uk/SGP2017/slides/Rodola_MachineLearningMeetsGeometry_SGP.pdf
• Geometric deep learning on graphs and manifolds [ppt]
http://geometricdeeplearning.com/slides/NIPS-GDL.pdf
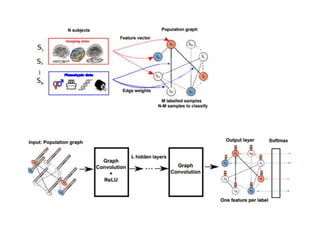
• Spectral Graph Convolutions for Population-based Disease Prediction
https://arxiv.org/pdf/1703.03020.pdf .
[Code@ https://github.com/parisots/population-gcn]
• Semi-supervised Classification with Graph Convolutional Networks
https://arxiv.org/pdf/1609.02907.pdf
• Geometric deep learning on graphs and manifolds using mixture model CNNs
https://arxiv.org/pdf/1611.08402.pdf

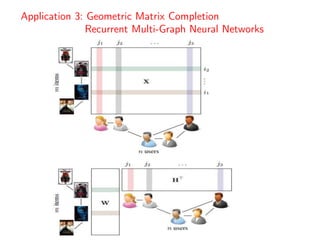
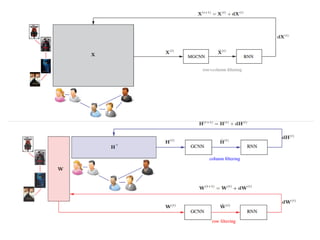
58. • Geometric Matrix Completion with Recurrent Multi-Graph Neural Networks
• https://arxiv.org/pdf/1704.06803v1.pdf
• [Code@ https://github.com/fmonti/mgcnn]
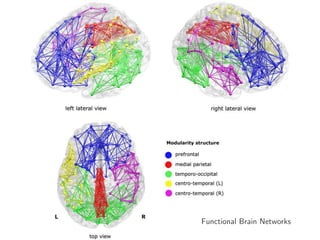
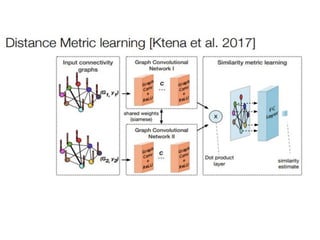
• Distance Metric Learning using Graph Convolutional Networks Application to Functional
Brain Networks
• https://arxiv.org/abs/1703.02161
• [Code@ https://github.com/sk1712/gcn_metric_learning]
Other code links:
• A tutorial on Graph Convolutional Neural Networks
https://github.com/dbusbridge/gcn_tutorial
• Graph-based Neural Networks
https://github.com/sungyongs/graph-based-nn
https://github.com/LeeDoYup/Graph-Convolutional-Networks
https://github.com/fps7806/Graph-CNN
• FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling
https://github.com/matenure/FastGCN
• Graph Convolutional Networks in PyTorch
https://github.com/tkipf/pygcn
• Graph Convolutional Networks
https://github.com/tkipf/gcn
Note: The images/equations used in the slides are borrowed from either Google images, Wikipedia or from respective
research papers/presentations