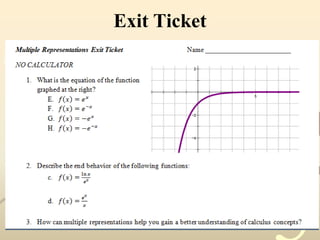
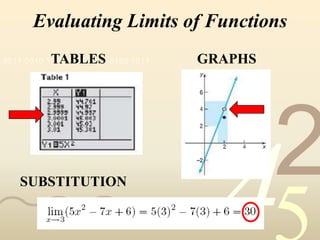
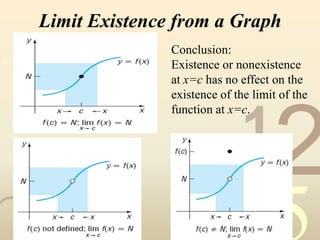
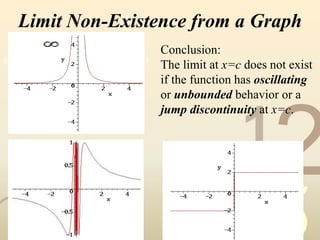
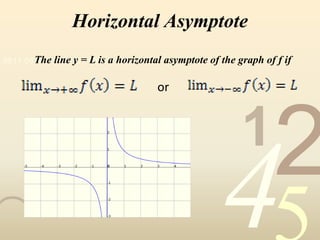
The document discusses several topics related to functions and limits in calculus: 1) It examines multiple representations of functions to familiarize students with properties of common functions like exponential, polynomial, and logarithmic functions. 2) It discusses using tables, graphs, and algebraic manipulations to evaluate limits, including limits at infinity and indeterminate forms. 3) It covers evaluating limits of rational functions and identifying horizontal asymptotes from graphs or formulas. The document provides examples and explanations of limits concepts to help students learn.

1. Objective: SWBAT examine multiple representations of
a function in order to become familiar with properties
of common functions
0011 0010 1010 1101 0001 0100 1011
DRILL: August 30, 2011
My Expectations of Calculus…
0011 0010 1010 1101 0001 0100 1011
•Why did you sign up for calculus? 1
2
4
•What do you expect the year to be like?
•What are your plans after high school that
involve mathematics or science-related
fields?

2. 0011 0010 1010 1101 0001 0100 1011
1
2
4
This lab assignment can be found on EDLINE.

3. The Dominance of Functions
• Any exponential function of n dominates any
0011 0010 1010 1101 0001 0100 1011
polynomial function of n.
• Any polynomial function of n dominates and
logarithmic function of n.
• Any logarithmic function of n dominates a
constant term. 1
2
• Any polynomial of degree k dominates a
polynomial of degree l if and only if k>l
4
In general, x(n) dominates y(n) if and only if
grows large.
grows as n

4. Exit Ticket
0011 0010 1010 1101 0001 0100 1011
1
2
4

5. Homework
0011 0010 1010 1101 0001 0100 1011
Mathematical Autobiography
• Typed
• Double-spaced
• Times Roman, 12 Font
1
2
4
• 4 paragraphs (as outlined on worksheet)
(one paragraph was done as today’s drill)

6. Objective: SWBAT use area representations in order to
evaluate limits using tables, graphs, and functions
0011 0010 1010 1101 0001 0100 1011
DRILL QUIZ #1: September 1, 2011
0011 0010 1010 1101 0001 0100 1011
1
2
4

7. 0011 0010 1010 1101 0001 0100 1011
1
2
4
This lab assignment can be found on EDLINE.

8. Evaluating Limits of Functions
TABLES
0011 0010 1010 1101 0001 0100 1011 GRAPHS
1
2
SUBSTITUTION
4

9. Limit Existence from a Graph
Conclusion:
0011 0010 1010 1101 0001 0100 1011
Existence or nonexistence
at x=c has no effect on the
existence of the limit of the
2
function at x=c.
1
4

10. Limit Non-Existence from a Graph
Conclusion:
0011 0010 1010 1101 0001 0100 1011
The limit at x=c does not exist
if the function has oscillating
or unbounded behavior or a
2
jump discontinuity at x=c.
1
4

11. Exit Ticket
0011 0010 1010 1101 0001 0100 1011
1
2
4

12. Homework
0011 0010 1010 1101 0001 0100 1011
Calculus Textbook
• Pgs. 54-58
• #’s 2, 7, 8, 9-18, 20, 26, 60, 63, 65, 66
1
2
4
• Pg. 67
• Choose one from #’s 11-22

13. Objective: SWBAT use direct substitution and other
algebraic manipulations in order to evaluate limits
0011 0010 1010 1101 0001 0100 1011
DRILL QUIZ #2: September 6, 2011
0011 0010 1010 1101 0001 0100 1011
1
2
4

14. The Indeterminate Form
• This limit cannot be determined
0011 0010 1010 1101 0001 0100 1011
• But this does not mean that the limit DNE
1
2
When this happens, try the following:
• Factor
4
• Rationalize the numerator or denominator
• Use Trig Substitutions to rewrite the function

15. Exit Ticket
0011 0010 1010 1101 0001 0100 1011
Evaluating Limits
Worksheet
1
2
4

16. Homework
0011 0010 1010 1101 0001 0100 1011
Calculus Textbook
• Pgs. 67-69
• #’s 24, 27, 35, 42, 44, 52, 54, 65, 67, 70, 77,
97, 98
1
2
4
• Prove the 2nd Special Trig Limit involving
cosine

17. Objective: SWBAT examine the area of regular
polygons in order to evaluate limits at infinity
DRILL QUIZ #3: September 8, 2011
0011 0010 1010 1101 0001 0100 1011
0011 0010 1010 1101 0001 0100 1011
1
2
4

18. 0011 0010 1010 1101 0001 0100 1011
1
2
4
This lab assignment can be found on EDLINE.

19. Horizontal Asymptote
0011 0010 1010 1101 0001 a horizontal
The line y = L is 0100 1011 asymptote of the graph of f if
or
1
2
4

20. Limits at Infinity of Rational Functions
• If the degree of the numerator is less than the
0011 0010 1010 1101 0001 0100 1011
degree of the denominator, then the limit of
the rational function is 0.
• If the degree of the numerator is equal to the
1
degree of the denominator, then the limit of
2
the rational function is the ratio of the leading
coefficients.
4
• If the degree of the numerator is greater than
the degree of the denominator, then the limit
of the rational function does not exist.

21. Exit Ticket
0011 0010 1010 1101 0001 0100 1011
1
2
4

22. Homework
0011 0010 1010 1101 0001 0100 1011
Calculus Textbook
• Pgs. 205-207
• #’s 1-8, 15-20, 88b
1
2
4