babiker biko, profile picture
Uploaded bybabiker biko
PPT, PDF7,766 views

القطوع المخروطية Conicss

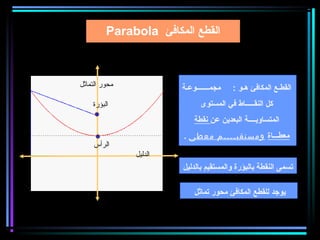
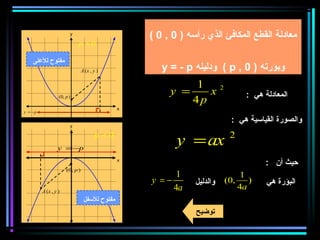
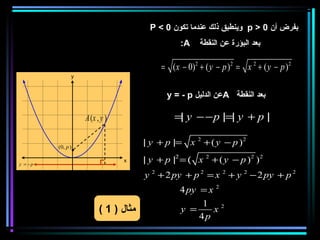
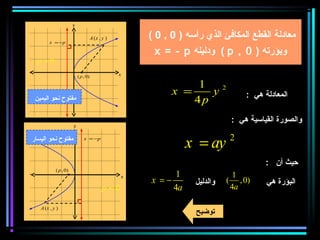
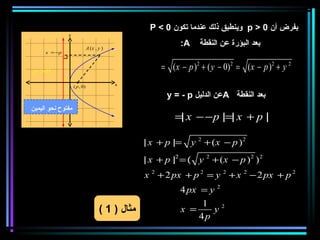
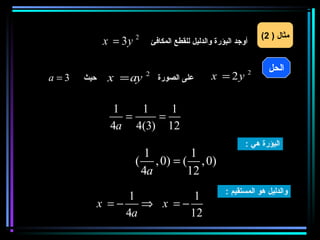
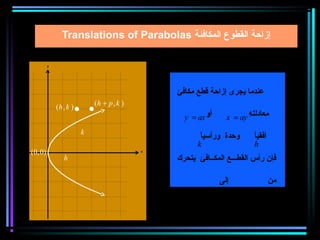
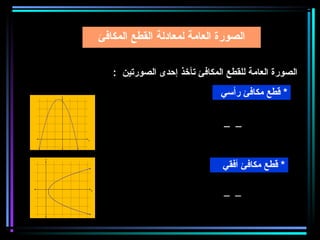
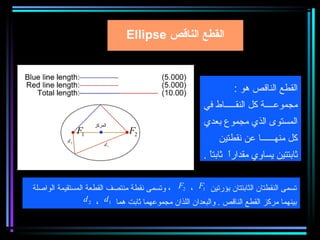
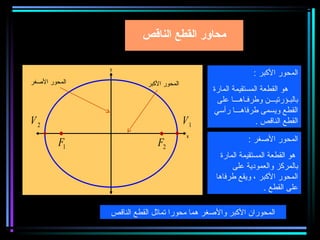
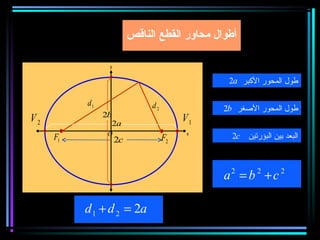
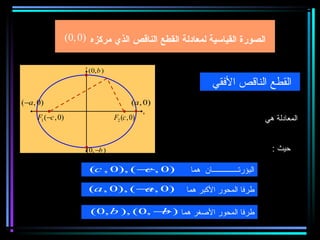
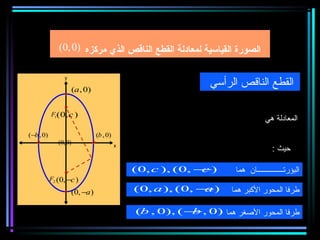
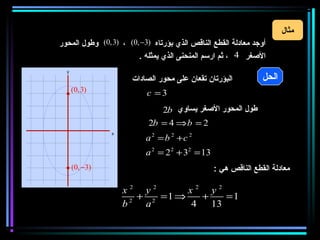
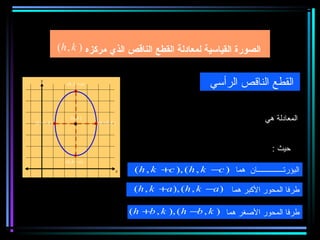
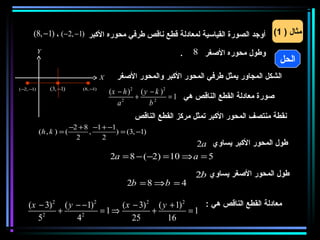
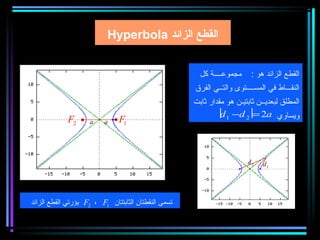
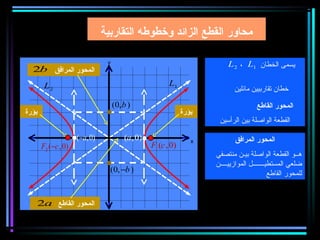
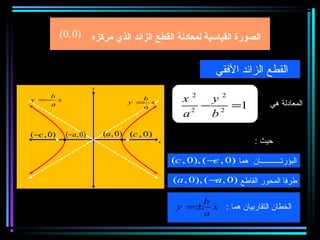
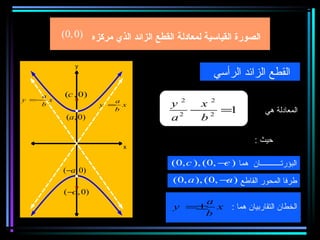
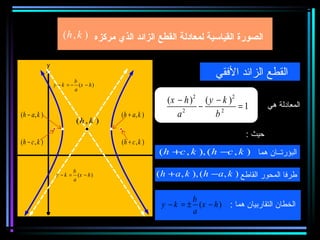
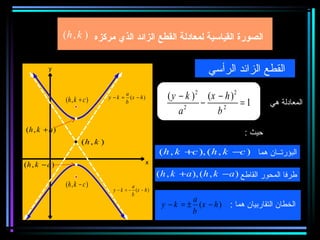
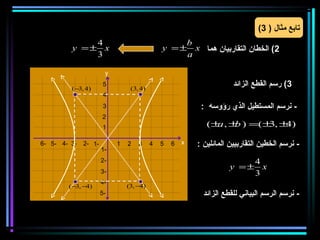
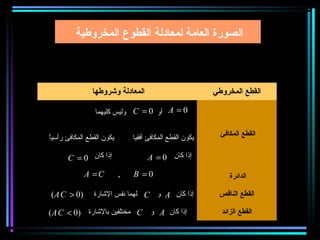
القطع المكافئ هو مجموعة من النقاط المتساوية البعد عن بؤرة ومستقيم يسمى الدليل، ويستخدم في بناء معادلات لتحديد خصائصه. يتضمن المستند أيضًا شروحات عن القطع الناقص والقطع الزائد مع أمثلة توضيحية لكيفية حساب المعادلات المختلفة. كما يشرح كيفية إزاحة القطوع المكافئة وتأثيرها على المعادلات الأساسية.

Embed presentation

Downloaded 107 times
‫القطع المكافئ‬ ‫مقدمة‬ ‫القطع الزائد‬ ‫القطع الناقص‬ ‫مواقع مفيدة‬ ‫مصطلحات رياضية‬
‫القطوع المخروطية ‪Conic Sections‬‬ ‫إذا قطع مستوى مخروطين‬ ‫قائمين مقلوبين ل نهائيين في‬ ‫أوضاع واتجاهات مختلفة فإننا‬ ‫نحصل على قطوع مختلفة تسمى‬ ‫قطوعا مخروطية .‬ ‫ ً‬
‫القطع المكافئ ‪Parabola‬‬ ‫محور التماثل‬ ‫مجمـــــــوعـة‬ ‫القطـع المكافئ هـو :‬ ‫البؤرة‬ ‫كل النقـــــاط في المستوى‬ ‫المتساويــــة البعدين عن نقطة‬ ‫معطـــاة ومستقيــــم معطى .‬ ‫الرأس‬ ‫الدليل‬ ‫تسمى النقطة بالبؤرة والمستقيم بالدليل‬ ‫يوجد للقطع المكافئ محور تماثل‬
‫‪y‬‬ ‫معادلة القطع المكافئ الذي رأسه ) 0 , 0 (‬ ‫0> ‪p‬‬ ‫مفتوح للعلى‬ ‫) ‪A (x , y‬‬ ‫) ‪A (x , y‬‬ ‫وبؤرته ) 0 , ‪ ( p‬ودليله ‪y = - p‬‬ ‫1‬ ‫= ‪y‬‬ ‫‪x‬‬ ‫2‬ ‫المعادلة هي :‬ ‫) ‪(0, p‬‬ ‫‪4p‬‬ ‫‪x‬‬ ‫‪y = −p‬‬ ‫والصورة القياسية هي :‬ ‫‪y‬‬ ‫‪y =−p‬‬ ‫0< ‪p‬‬ ‫‪y = ax‬‬ ‫2‬ ‫‪x‬‬ ‫حيث أن :‬ ‫) ‪(0, p‬‬ ‫1‬ ‫1‬ ‫−= ‪y‬‬ ‫والدليل‬ ‫,0(‬ ‫)‬ ‫البؤرة هي‬ ‫) ‪A (x , y‬‬ ‫‪4a‬‬ ‫‪4a‬‬ ‫مفتوح للسفل‬ ‫توضيح‬
‫بفرض أن 0 > ‪ p‬وينطبق ذلك عندما تكون 0 < ‪P‬‬ ‫‪:A‬‬ ‫بعد البؤرة عن النقطة‬ ‫) ‪A (x , y‬‬ ‫2 ) ‪= (x − 0) 2 + ( y − p ) 2 = x 2 + ( y − p‬‬ ‫‪y‬‬ ‫بعد النقطة ‪A‬عن الدليل ‪y = - p‬‬ ‫) ‪A (x , y‬‬ ‫| ‪=| y − − p |=| y + p‬‬ ‫) ‪(0, p‬‬ ‫2 ) ‪| y + p |= x 2 + ( y − p‬‬ ‫‪y = −p‬‬ ‫‪x‬‬ ‫2 ) 2 ) ‪| y + p |2 = ( x 2 + ( y − p‬‬ ‫2 ‪y 2 + 2 py + p 2 = x 2 + y 2 − 2 py + p‬‬ ‫2 ‪−− − −−4 py = x‬‬ ‫2 1‬ ‫= ‪ −− − − −y‬مثال ) 1 (‬ ‫‪x‬‬ ‫‪4p‬‬
‫أوجد معادلة القطع المكافئ الذي بؤرته )2− ,0( ودليله 2 = ‪y‬‬ ‫مثال ) 1 (‬ ‫) ‪A (x , y‬‬ ‫الحل‬ ‫1‬ ‫1‬ ‫1−‬ ‫,0( = )2− ,0(‬ ‫= 2 −−⇒ )‬ ‫= ‪⇒a‬‬ ‫‪4a‬‬ ‫‪4a‬‬ ‫8‬ ‫2 1−‬ ‫‪y = ax ⇒ y = x‬‬ ‫2‬ ‫8‬ ‫مثال ) 2 (‬
‫أوجد البؤرة والدليل للقطع المكافئ 2 ‪y = 2x‬‬ ‫مثال ) 2(‬ ‫) ‪A (x , y‬‬ ‫الحل‬ ‫2=‪a‬‬ ‫حيث‬ ‫‪y = ax‬‬ ‫2‬ ‫على الصورة‬ ‫‪y = 2x‬‬ ‫2‬ ‫1‬ ‫1‬ ‫1‬ ‫=‬ ‫=‬ ‫8 )2(4 ‪4a‬‬ ‫1‬ ‫1‬ ‫البؤرة هي :‬ ‫,0(‬ ‫) ,0( = )‬ ‫‪4a‬‬ ‫8‬ ‫1‬ ‫1‬ ‫والدليل هو المستقيم :‬ ‫مثال ) 3(‬ ‫−= ‪y‬‬ ‫− = ‪⇒ −y‬‬ ‫‪4a‬‬ ‫8‬
‫أوجد في الصورة القياسية معادلة القطع المكافئ حيث دليله‬ ‫مثال ) 3(‬ ‫هو المستقيم 4− = ‪ y‬وبؤرته )4 ,0(‬ ‫) ‪A (x , y‬‬ ‫الحل‬ ‫وهو مستقيم أفقي والبؤرة تقع إلى العلى‬ ‫الدليل هو 4− = ‪y‬‬ ‫القطع له خط تماثل رأسي ومفتوح إلى العلى‬ ‫1‬ ‫1‬ ‫− = ‪−y‬‬ ‫= ‪= −4 ⇒ −a‬‬ ‫‪4a‬‬ ‫61‬ ‫2 1‬ ‫‪y = ax − ⇒ − y = x‬‬ ‫2‬ ‫61‬
‫‪y‬‬ ‫) ‪A (x , y‬‬ ‫معادلة القطع المكافئ الذي رأسه ) 0 , 0 (‬ ‫‪x = −p‬‬ ‫) ‪A (x , y‬‬ ‫وبؤرته ) 0 , ‪ ( p‬ودليله ‪x = - p‬‬ ‫0> ‪p‬‬ ‫)0 , ‪( p‬‬ ‫‪x‬‬ ‫1‬ ‫= ‪x‬‬ ‫‪y‬‬ ‫2‬ ‫المعادلة هي :‬ ‫مفتوح نحو اليمين‬ ‫‪4p‬‬ ‫والصورة القياسية هي :‬ ‫‪y‬‬ ‫مفتوح نحو اليسار‬ ‫‪x = −p‬‬ ‫‪x = ay‬‬ ‫2‬ ‫حيث أن :‬ ‫)0 , ‪( p‬‬ ‫1‬ ‫1‬ ‫−= ‪x‬‬ ‫‪x‬‬ ‫والدليل‬ ‫(‬ ‫)0 ,‬ ‫البؤرة هي‬ ‫0< ‪p‬‬ ‫‪4a‬‬ ‫‪4a‬‬ ‫) ‪A (x , y‬‬ ‫توضيح‬
‫بفرض أن 0 > ‪ p‬وينطبق ذلك عندما تكون 0 < ‪P‬‬ ‫‪y‬‬ ‫) ‪A (x , y‬‬ ‫‪:A‬‬ ‫بعد البؤرة عن النقطة‬ ‫‪x = −p‬‬ ‫0> ‪p‬‬ ‫) ‪A (x , y‬‬ ‫2 ‪= (x − p ) 2 + ( y − 0) 2 = (x − p )2 + y‬‬ ‫)0 , ‪( p‬‬ ‫‪x‬‬ ‫بعد النقطة ‪A‬عن الدليل ‪y = - p‬‬ ‫مفتوح نحو اليمين‬ ‫| ‪=| x − − p |=| x + p‬‬ ‫=| ‪| x + p‬‬ ‫2 ) ‪y 2 + (x − p‬‬ ‫2 ) 2 ) ‪| x + p |2 = ( y 2 + (x − p‬‬ ‫2 ‪x 2 + 2 px + p 2 = y 2 + x 2 − 2 px + p‬‬ ‫2 ‪−− −−−4 px = y‬‬ ‫1‬ ‫= ‪ −− − − −x‬مثال ) 1 (‬ ‫2‪y‬‬ ‫‪4p‬‬
‫1‬ ‫1‬ ‫مثال ) 1 (‬ ‫−= ‪x‬‬ ‫أوجد معادلة القطع المكافئ الذي بؤرته )0 , ( ودليله‬ ‫4‬ ‫4‬ ‫الحل‬ ‫1‬ ‫1‬ ‫1‬ ‫1‬ ‫(‬ ‫− ⇒ )0 , ( = )0 ,‬ ‫1 = ‪= ⇒a‬‬ ‫‪4a‬‬ ‫4‬ ‫4 ‪4a‬‬ ‫‪x = ay‬‬ ‫2‬ ‫‪x = 1y‬‬ ‫2‬ ‫مثال ) 2 (‬ ‫‪x =y‬‬ ‫2‬
‫مثال ) 2(‬ ‫‪x = 3y‬‬ ‫2‬ ‫أوجد البؤرة والدليل للقطع المكافئ‬ ‫) ‪A (x , y‬‬ ‫الحل‬ ‫3= ‪a‬‬ ‫حيث‬ ‫‪x = ay‬‬ ‫2‬ ‫على الصورة‬ ‫‪x = 2y‬‬ ‫2‬ ‫1‬ ‫1‬ ‫1‬ ‫=‬ ‫=‬ ‫21 )3(4 ‪4a‬‬ ‫البؤرة هي :‬ ‫1‬ ‫1‬ ‫)0 , ( = )0 , (‬ ‫‪4a‬‬ ‫21‬ ‫والدليل هو المستقيم :‬ ‫1‬ ‫1‬ ‫− = ‪x = − ⇒ −x‬‬ ‫‪4a‬‬ ‫21‬
‫إزاحة القطوع المكافئة ‪Translations of Parabolas‬‬ ‫‪y‬‬ ‫عندما يجرى إزاحة قطع مكافئ‬ ‫) ‪(h + p , k‬‬ ‫) ‪(h , k‬‬ ‫أو ‪y = ax‬‬ ‫2‬ ‫معادلته ‪x = ay‬‬ ‫2‬ ‫‪k‬‬ ‫) ‪(h , k‬‬ ‫ ً‬ ‫وحدة ورأسيا‬ ‫ ً‬ ‫أفقيا‬ ‫‪k‬‬ ‫‪h‬‬ ‫)0 ,0(‬ ‫) ‪(h + p , k‬‬ ‫‪x‬‬ ‫‪h‬‬ ‫فإن رأس القطـــع المكــافئ يتحرك‬ ‫إلى‬ ‫من‬ ‫) ‪(h , k‬‬ ‫)0 ,0(‬
‫الصورة القياسية لمعادلة القطع المكافئ الذي رأسه ) ‪(h , k‬‬ ‫الصورة القياسية لمعادلة‬ ‫البؤرة ومعادلة الدليل‬ ‫القطع المكافئ‬ ‫1‬ ‫+ ‪(h , k‬‬ ‫)‬ ‫‪4a‬‬ ‫2 ) ‪y − k = a (x − h‬‬ ‫1‬ ‫− ‪y =k‬‬ ‫‪4a‬‬ ‫1‬ ‫+ ‪(h‬‬ ‫) ‪,k‬‬ ‫‪4a‬‬ ‫1‬ ‫2) ‪x − h = a ( y − k‬‬ ‫− ‪x =h‬‬ ‫‪4a‬‬
‫أوجد الصورة القياسية لمعادلة القطع المكافئ الذي رأسه )4 ,3( وبؤرته )4 ,5(‬ ‫مثال ) 1(‬ ‫بما أن الرأس والبؤرة يقعان على خط أفقي ، والبؤرة إلى يمين الرأس‬ ‫الحل‬ ‫يكون القطع المكافئ مفتوحا إلى اليمين وصورة معادلته 2 ) ‪x − h = a ( y − k‬‬ ‫الرأس هو ) ‪( h , k‬‬ ‫4 = ‪( h , k ) = (3, 4) ⇒ h = 3, k‬‬ ‫1‬ ‫+ ‪(h‬‬ ‫البؤرة هي ) ‪, k‬‬ ‫1‬ ‫1‬ ‫‪4a‬‬ ‫+ ‪(h‬‬ ‫+ ⇒ )4 ,5(= ) ‪, k‬‬ ‫3‬ ‫5=‬ ‫‪4a‬‬ ‫‪4a‬‬ ‫1‬ ‫=‪a‬‬ ‫8‬ ‫الصورة القياسية لمعادلة القطع المكافئ هي :‬ ‫1‬ ‫2 )4 − ‪x − 3 = ( y‬‬ ‫8‬
‫الصورة العامة لمعادلة القطع المكافئ‬ ‫الصورة العامة للقطع المكافئ تأخذ إحدى الصورتين :‬ ‫‪y‬‬ ‫* قطع مكافئ رأسي‬ ‫0 ≠ ‪y = ax +bx + c − , − a‬‬ ‫2‬ ‫‪x‬‬ ‫‪y‬‬ ‫* قطع مكافئ أفقي‬ ‫0 ≠ ‪x = ay + by + c − , −a‬‬ ‫2‬ ‫‪x‬‬
‫هي لقطع مكافئ ؟‬ ‫0 = 6 − ‪x 2 − 4x + 2 y‬‬ ‫هل المعادلة‬ ‫مثال ) 1(‬ ‫إذا كانت كذلك ، فأوجد الرأس والبؤرة والدليل .‬ ‫بما أن المعادلة تربيعية في المتغير ‪x‬‬ ‫الحل‬ ‫نكمل المربع بالنسبة إلى ‪ x‬لنحصل على الصورة القياسية‬ ‫6 + ‪x 2 − 4x + 2 y − 6 = 0 ⇒ x 2 − 4x = −2 y‬‬ ‫2 4−‬ ‫2 4−‬ ‫‪x‬‬ ‫2‬ ‫( + ‪− 4x‬‬ ‫( + 6 + ‪) = −2 y‬‬ ‫01+ ‪) ⇒( x − 2) 2 = −2 y‬‬ ‫2‬ ‫2‬ ‫−‬‫1‬ ‫وهذه المعادلة على الصورة ) ‪( y − k ) = a ( x − h‬‬ ‫2‬ ‫= )5− ‪( y‬‬ ‫2 )2− ‪(x‬‬ ‫2‬ ‫1−‬ ‫= ‪h = 2−, −k = 5, −a‬‬ ‫2‬ ‫1‬ ‫1‬ ‫9‬ ‫+ ‪(h , k‬‬ ‫+ 5 ,2(= )‬ ‫−‬ ‫1‬ ‫) ,2(= )‬ ‫والبؤرة هي :‬ ‫الرأس هو : )5,2(‬ ‫‪4a‬‬ ‫(4‬ ‫)‬ ‫2‬ ‫2‬ ‫1‬ ‫1‬ ‫11‬ ‫− ‪y =k‬‬ ‫− 5=‬ ‫= ‪⇒y‬‬ ‫والدليل هو :‬ ‫‪4a‬‬ ‫−‬ ‫1‬ ‫2‬ ‫(4‬ ‫)‬ ‫2‬
‫تدريبات‬ ‫تدريب ) 1(‬ ‫عين الرأس ، والبؤرة ، ومعادلة محور التماثل ومعادلة الدليل للقطع المكافئ‬ ‫نّ‬ ‫)2 − ‪( y + 1) 2 = 4(x‬‬ ‫تدريب ) 2(‬ ‫1= ‪y‬‬ ‫اكتب معادلة القطع المكافئ الذي رأسه النقطة )4− ,2( ومعادلة دليله هي‬ ‫عند النقطة )4 ,1(‬ ‫‪y 2 = 16x‬‬ ‫تدريب ) 3(‬ ‫أوجد معادلة المماس لمنحنى القطع المكافئ‬
‫القطع الناقص ‪Ellipse‬‬ ‫القطع الناقص هو :‬ ‫مجموعــــة كل النقـــــاط في‬ ‫2‪F‬‬ ‫المركز‬ ‫1‪F‬‬ ‫المستوى الذي مجموع بعدي‬ ‫1‪F‬‬ ‫2‪F‬‬ ‫2‪d‬‬ ‫1‪d‬‬ ‫كل منهــــــا عن نقطتين‬ ‫ثابتتين يساوي مقدارا ثابتا .‬ ‫ ً‬ ‫ ً‬ ‫تسمى النقطتان الثابتتان بؤرتين 1‪ ، F2 ، F‬وتسمى نقطة منتصف القطعة المستقيمة الواصلة‬ ‫بينهما مركز القطع الناقص . والبعدان اللذان مجموعهما ثابت هما 1 ‪d 2 ، d‬‬
‫محاور القطع الناقص‬ ‫‪y‬‬ ‫المحور الكبر :‬ ‫المحور الصغر‬ ‫المحور الكبر‬ ‫هو القطعة المستقيمة المارة‬ ‫بالبـؤرتيـــن وطرفـاهـــا على‬ ‫القطع ويسمى طرفاهـــا رأسي‬ ‫2‪V‬‬ ‫2‪F‬‬ ‫1‪F‬‬ ‫1‪V‬‬ ‫القطع الناقص .‬ ‫‪x‬‬ ‫1‪F‬‬ ‫2‪F‬‬ ‫المحور الصغر :‬ ‫هو القطعة المستقيمة المارة‬ ‫بالمركز والعمودية على‬ ‫المحور الكبر ، ويقع طرفاها‬ ‫على القطع .‬ ‫المحوران الكبر والصغر هما محورا تماثل القطع الناقص‬
‫أطوال محاور القطع الناقص‬ ‫‪y‬‬ ‫طول المحور الكبر ‪2a‬‬ ‫1‪d‬‬ ‫2‪d‬‬ ‫طول المحور الصغر ‪2b‬‬ ‫‪2b‬‬ ‫2‪V‬‬ ‫‪2a‬‬ ‫1‪V‬‬ ‫‪O‬‬ ‫‪x‬‬ ‫البعد بين البؤرتين ‪2c‬‬ ‫1‪F‬‬ ‫‪2c‬‬ ‫2‪F‬‬ ‫2 ‪a2 = b 2 + c‬‬ ‫‪d 1 + d 2 = 2a‬‬
‫الصورة القياسية لمعادلة القطع الناقص الذي مركزه )0 ,0(‬ ‫‪y‬‬ ‫) ‪(0, b‬‬ ‫القطع الناقص الفقي‬ ‫)0 , ‪( −a‬‬ ‫2‪F‬‬ ‫1‪F‬‬ ‫)0 , ‪(a‬‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫1= 2 +‬ ‫‪x‬‬ ‫)0 , ‪F1 (−c‬‬ ‫)0 ,0(‬ ‫)0, ‪F2 (c‬‬ ‫المعادلة هي‬ ‫2‬ ‫‪a‬‬ ‫‪b‬‬ ‫) ‪(0, −b‬‬ ‫‪a >b‬‬ ‫حيث :‬ ‫)0 ,− ( ,)0 , ‪(c‬‬ ‫‪c‬‬ ‫البؤرتــــــــــــــان هما‬ ‫)0 ,− ( ,)0 , ‪(a‬‬ ‫‪a‬‬ ‫طرفا المحور الكبر هما‬ ‫طرفا المحور الصغر هما ) − ,0( ,) ‪(0, b‬‬ ‫‪b‬‬
‫الصورة القياسية لمعادلة القطع الناقص الذي مركزه )0 ,0(‬ ‫‪y‬‬ ‫)0 , ‪(a‬‬ ‫القطع الناقص الرأسي‬ ‫) ‪F1(0, c‬‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫2‬ ‫1= 2 +‬ ‫المعادلة هي‬ ‫)0 , ‪(−b‬‬ ‫)0 , ‪(b‬‬ ‫‪b‬‬ ‫‪a‬‬ ‫)0 ,0(‬ ‫‪x‬‬ ‫‪a >b‬‬ ‫حيث :‬ ‫)− ,0( ,) ‪(0, c‬‬ ‫‪c‬‬ ‫البؤرتــــــــــــــان هما‬ ‫) ‪F2 (0, −c‬‬ ‫) ‪(0, −a‬‬ ‫)− ,0( ,) ‪(0, a‬‬ ‫‪a‬‬ ‫طرفا المحور البكبر هما‬ ‫طرفا المحور الغصغر هما )0 ,− ( ,)0 , ‪(b‬‬ ‫‪b‬‬
‫مثال‬ ‫أوجد معادلة القطع الناقص الذي بؤرتاه )3− ,0( ، )3,0( وطول المحور‬ ‫الغصغر 4 ، ثم ارسم المنحنى الذي يمثله .‬ ‫‪y‬‬ ‫البؤرتان تقعان على محور الصادات‬ ‫الحل‬ ‫)3,0(‬ ‫3= ‪c‬‬ ‫طول المحور الغصغر يساوي ‪2b‬‬ ‫2 = ‪2b = 4 ⇒ b‬‬ ‫‪x‬‬ ‫2 ‪a 2 = b 2 +c‬‬ ‫31 = 23 + 2 2 = 2 ‪a‬‬ ‫)3− ,0(‬ ‫معادلة القطع الناقص هي :‬ ‫2‪x2 y‬‬ ‫2‪x2 y‬‬ ‫2‬ ‫⇒ 1= 2 +‬ ‫+‬ ‫1=‬ ‫‪b‬‬ ‫‪a‬‬ ‫4‬ ‫31‬
‫الصورة القياسية لمعادلة القطع الناقص الذي مركزه ) ‪(h , k‬‬ ‫‪y‬‬ ‫) ‪(h , k + b‬‬ ‫القطع الناقص الفقي‬ ‫) ‪(h − a, k‬‬ ‫) ‪(h , k‬‬ ‫) ‪(h + a , k‬‬ ‫2 ) ‪(x − h ) 2 ( y − k‬‬ ‫المعادلة هي‬ ‫2‬ ‫+‬ ‫2‬ ‫1=‬ ‫) ‪(h , k − b‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫‪x‬‬ ‫‪a >b‬‬ ‫حيث :‬ ‫البؤرتــــــــــــــان هما ) ‪( h + , k ), ( h − , k‬‬ ‫‪c‬‬ ‫‪c‬‬ ‫طرفا المحور البكبر هما ) ‪(h + a , k ), (h −a , k‬‬ ‫‪c = a −b‬‬ ‫2‬ ‫2‬ ‫2‬ ‫طرفا المحور الغصغر هما ) ‪( h , k +b ), (h , k −b‬‬
‫الصورة القياسية لمعادلة القطع الناقص الذي مركزه ) ‪(h , k‬‬ ‫) ‪(h , k + a‬‬ ‫القطع الناقص الرأسي‬ ‫2 ) ‪(x − h ) 2 ( y − k‬‬ ‫) ‪(h − b , k‬‬ ‫) ‪(h , k‬‬ ‫) ‪(h + b , k‬‬ ‫2‬ ‫+‬ ‫2‬ ‫1=‬ ‫المعادلة هي‬ ‫‪b‬‬ ‫‪a‬‬ ‫‪a >b‬‬ ‫حيث :‬ ‫) ‪(h , k − a‬‬ ‫البؤرتــــــــــــــان هما ) ‪( h , k +c ), ( h , k −c‬‬ ‫طرفا المحور البكبر هما ) ‪( h , k +a ), ( h , k −a‬‬ ‫2 ‪c 2 = a 2 −b‬‬ ‫طرفا المحور الغصغر هما ) ‪( h +b , k ), ( h −b , k‬‬
‫مثال ) 1( أوجد الصورة القياسية لمعادلة قطع ناقص طرفي محوره الكبر )1− ,2−( ، )1− ,8(‬ ‫‪Y‬‬ ‫.‬ ‫وطول محوره الغصغر 8‬ ‫الحل‬ ‫‪X‬‬ ‫الشكل المجاور يمثل طرفي المحور الكبر والمحور الغصغر‬ ‫)1− ,3(‬ ‫)1− −(‬ ‫,2‬ ‫− ,8(‬‫)1‬ ‫2) ‪(x − h )2 ( y − k‬‬ ‫2‬ ‫+‬ ‫2‬ ‫غصورة معادلة القطع الناقص هي 1 =‬ ‫‪a‬‬ ‫‪b‬‬ ‫نقطة منتصف المحور الكبر تمثل مركز القطع الناقص‬ ‫1− + 1− 8 + 2−‬ ‫( = ) ‪(h , k‬‬ ‫,‬ ‫)1− ,3( = )‬ ‫2‬ ‫2‬ ‫طول المحور الكبر يساوي ‪2a‬‬ ‫5 = ‪2a = 8 − (−2) = 10 ⇒ a‬‬ ‫طول المحور الغصغر يساوي ‪2b‬‬ ‫4 = ‪2b = 8 ⇒ b‬‬ ‫2 )1− − ‪(x − 3) 2 ( y‬‬ ‫2 )1 + ‪( x − 3) 2 ( y‬‬ ‫معادلة القطع الناقص هي :‬ ‫2‬ ‫+‬ ‫2‬ ‫⇒1 =‬ ‫+‬ ‫1=‬ ‫5‬ ‫4‬ ‫52‬ ‫61‬
‫2 )1 + ‪(x − 4) 2 ( y‬‬ ‫+‬ ‫1=‬ ‫مثال ) 2( ارسم شكل تقريبيا للقطع الناقص‬ ‫52‬ ‫961‬ ‫من معادلة القطع الناقص نلظحظ أن مركز القطع هو : − ,4(= ) ‪( h , k‬‬ ‫)1‬ ‫الحل‬ ‫ومن المعادلة أيضا نلظحظ أن 961< 52 أي أن المحور الكبر يكون رأسيا‬ ‫ً‬ ‫‪y‬‬ ‫)21,4(‬ ‫31= ⇒ 961= 2 ‪a‬‬ ‫‪a‬‬ ‫)11,4(‬ ‫وهذا يعني أن نقطتي طرفي المحور الكبر تبعدان 31 وظحدة‬ ‫أسفل وأعلى المركز أي عند النقطتين )41− ,4( و )21,4(‬ ‫5= ⇒ 52 = 2 ‪b‬‬ ‫‪b‬‬ ‫‪x‬‬ ‫)1 − ,1 −(‬ ‫)1 − ,9(‬ ‫)1 − ,4(‬ ‫وهذا يعني أن نقطتي طرفي المحور الغصغر تبعدان 5 وظحدات‬ ‫إلى يسار ويمين المركز أي عند النقطتين )1− ,1−( و − ,9(‬ ‫)1‬ ‫)31 − ,4(‬ ‫21 = 52 − 961 = ‪c 2 = a 2 − b 2 ⇒ c‬‬ ‫)41 − ,4(‬ ‫وهذا يعني أن البؤرتان تبعدان 21 وظحدة أسفل‬ ‫وأعلى المركز أي عند النقطتين )31− ,4( و )11,4(‬
‫تدريبات‬ ‫أثبت أن المعادلة 0 = 4 − ‪x 2 + 2 y 2 − 4x + 8 y‬‬ ‫تدريب )1(‬ ‫تمثل قطعا ناقصا .‬ ‫ً‬ ‫ً‬ ‫تدريب ) 2(‬ ‫جد معادلة القطع الناقص الذي مركزه )2 ,2( وإظحدى بؤرتيه النقطة )2 ,1−(‬ ‫وطول محوره الكبر 01 2 وظحدة .‬ ‫أوجد معادلة المماس لمنحنى القطع الناقص 8 = 2 ‪ x 2 + y‬عند النقطة )1,2−(‬ ‫تدريب ) 3(‬
‫القطع الزائد ‪Hyperbola‬‬ ‫مجموعــــة بكل‬ ‫القطع الزائد هو :‬ ‫النقـــاط في المســــتوى والتــي الفرق‬ ‫المطلق لبعديــن ثابتيـن هو مقدار ثابت‬ ‫ويساوي ‪ 1 −d 2 2a‬‬ ‫‪d‬‬ ‫=‬ ‫2‪F‬‬ ‫‪a‬‬ ‫‪a‬‬ ‫1‪F‬‬ ‫2‪d‬‬ ‫1‪d‬‬ ‫تسمى النقطتان الثابتتان 1‪ F2 ، F‬بؤرتي القطع الزائد‬
‫محاور القطع الزائد وخطوطه التقاربية‬ ‫‪y‬‬ ‫يسمى الخطان 1‪L 2 ، L‬‬ ‫المحور المرافق ‪2b‬‬ ‫2‪L‬‬ ‫1‪L‬‬ ‫خطان تقاربيين مائلين‬ ‫) ‪(0, b‬‬ ‫المحور القاطع‬ ‫بؤرة‬ ‫بؤرة‬ ‫القطعة الواغصلة بين الرأسين‬ ‫)0,‪(− a‬‬ ‫)0 ,‪(a‬‬ ‫‪x‬‬ ‫المحور المرافق‬ ‫)0, ‪F2 (−c‬‬ ‫)0 , ‪F1 (c‬‬ ‫هــو القطعة الواغصلة بيـن منتصفي‬ ‫ضلعي المستطيـــــــل الموازييــــن‬ ‫) ‪(0, −b‬‬ ‫للمحور القاطع‬ ‫المحور القاطع ‪2a‬‬ ‫‪c = a +b‬‬ ‫2‬ ‫2‬ ‫2‬
‫الصورة القياسية لمعادلة القطع الزائد الذي مركزه )0 ,0(‬ ‫القطع الزائد الفقي‬ ‫‪y‬‬ ‫‪b‬‬ ‫‪y =− x‬‬ ‫‪b‬‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫‪a‬‬ ‫‪y = x‬‬ ‫‪a‬‬ ‫2‬ ‫1= 2 −‬ ‫المعادلة هي‬ ‫)0 ,0(‬ ‫) ‪(x , y‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫)0 , −(‬ ‫‪c‬‬ ‫)0 , ‪(−a‬‬ ‫)0 , ‪(a , 0) (c‬‬ ‫‪x‬‬ ‫2 ‪c 2 = a2 + b‬‬ ‫حيث :‬ ‫البؤرتـــــــــــان هما )0 , − ( ,)0 , ‪(c‬‬ ‫‪c‬‬ ‫طرفا المحور القاطع )0 , − ( ,)0 , ‪(a‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫الخطان التقاربيان هما : ‪y =± x‬‬ ‫‪a‬‬
‫الصورة القياسية لمعادلة القطع الزائد الذي مركزه )0 ,0(‬ ‫) ‪(x , y‬‬ ‫‪y‬‬ ‫القطع الزائد الرأسي‬ ‫‪a‬‬ ‫)0 , ‪(c‬‬ ‫‪y =− x‬‬ ‫‪b‬‬ ‫‪a‬‬ ‫‪y = x‬‬ ‫2‪y‬‬ ‫2‪x‬‬ ‫‪b‬‬ ‫2‬ ‫1= 2 −‬ ‫المعادلة هي‬ ‫)0 , ‪(a‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫2 ‪c 2 = a2 + b‬‬ ‫حيث :‬ ‫‪x‬‬ ‫البؤرتـــــــــــان هما ) − ,0( ,) ‪(0, c‬‬ ‫‪c‬‬ ‫)0 , ‪(−a‬‬ ‫طرفا المحور القاطع ) − ,0( ,) ‪(0, a‬‬ ‫‪a‬‬ ‫)0 , −(‬ ‫‪c‬‬ ‫‪a‬‬ ‫‪y =± x‬‬ ‫الخطان التقاربيان هما :‬ ‫‪b‬‬
‫الصورة القياسية لمعادلة القطع الزائد الذي مركزه ) ‪(h , k‬‬ ‫‪y‬‬ ‫القطع الزائد الفقي‬ ‫‪b‬‬ ‫) ‪y − k = − (x − h‬‬ ‫‪a‬‬ ‫2) ‪(x − h )2 ( y − k‬‬ ‫2‬ ‫−‬ ‫2‬ ‫1=‬ ‫المعادلة هي‬ ‫) ‪(h − a, k‬‬ ‫) ‪(h + a, k‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫) ‪(h , k‬‬ ‫2 ‪c 2 = a2 +b‬‬ ‫حيث :‬ ‫) ‪(h − c , k‬‬ ‫) ‪(h + c , k‬‬ ‫البؤرتــان هما ) ‪( h +c , k ), ( h −c , k‬‬ ‫‪x‬‬ ‫‪b‬‬ ‫) ‪y − k = (x − h‬‬ ‫طرفا المحور القاطع ) ‪( h +a , k ), ( h −a , k‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫) ‪y − k = ± (x − h‬‬ ‫الخطان التقاربيان هما :‬ ‫‪a‬‬
‫الصورة القياسية لمعادلة القطع الزائد الذي مركزه ) ‪(h , k‬‬ ‫) ‪(x , y‬‬ ‫‪y‬‬ ‫القطع الزائد الرأسي‬ ‫) ‪(h , k + c‬‬ ‫‪a‬‬ ‫) ‪y − k = (x − h‬‬ ‫2) ‪( y − k ) 2 (x − h‬‬ ‫‪b‬‬ ‫2‬ ‫−‬ ‫2‬ ‫1=‬ ‫المعادلة هي‬ ‫‪a‬‬ ‫‪b‬‬ ‫) ‪(h , k + a‬‬ ‫حيث :‬ ‫2 ‪c 2 = a2 + b‬‬ ‫) ‪(h , k‬‬ ‫البؤرتــان هما ) ‪( h , k +c ), ( h , k −c‬‬ ‫) ‪(h , k − a‬‬ ‫‪x‬‬ ‫طرفا المحور القاطع ) ‪( h , k +a ), ( h , k −a‬‬ ‫) ‪(h , k − c‬‬ ‫‪a‬‬ ‫) ‪y − k = − (x − h‬‬ ‫‪b‬‬ ‫‪a‬‬ ‫) ‪y − k = ± (x − h‬‬ ‫الخطان التقاربيان هما :‬ ‫‪b‬‬
‫2‬ ‫2‬ ‫مثال ) 1(‬ ‫‪x‬‬ ‫‪y‬‬ ‫−‬ ‫عين بؤرتي وطرفي المحور القاطع وطولي المحورين للقطع الزائد 1 =‬ ‫نّ‬ ‫1‬ ‫4‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫الحل‬ ‫1= 2 −‬ ‫معادلة القطع على الصورة‬ ‫2‪a‬‬ ‫‪b‬‬ ‫2 = ‪a 2 = 4 ⇒a‬‬ ‫إذن‬ ‫1= ‪b 2 =1 ⇒b‬‬ ‫‪c‬‬ ‫نجد قيمة‬ ‫5 = ‪c = a +b ⇒c = a +b = 4 +1 ⇒c‬‬ ‫2‬ ‫2‬ ‫2‬ ‫2‬ ‫2‬ ‫(‬ ‫)0 ,5 − ( ,)0 ,5‬ ‫البؤرتــــان هما )0 , − ( ,)0 , ‪⇐ c‬‬ ‫(‬ ‫‪c‬‬ ‫)0 − ( ,)0 ,2(‬ ‫,2‬ ‫طرفا المحور القاطع )0 , − ( ,)0 , ‪⇐(a‬‬ ‫‪a‬‬ ‫= × = ‪2a‬‬ ‫2 2‬ ‫4‬ ‫⇐‬‫طول المحور القاطع يساوي ‪2a‬‬ ‫= × = ‪2a‬‬ ‫2 2‬ ‫4‬ ‫⇐‬‫طول المحور القاطع يساوي ‪2a‬‬
‫مثال ) 2(‬ ‫جد معادلة القطع الزائد الذي طول محوره المرافق 4 ، وبؤرتاه‬ ‫هما النقطتان )8 ± ,0(‬ ‫بما أن البؤرتين هما )8 ± ,0(‬ ‫الحل‬ ‫إذن البؤرتان تقعان على محور الصادات حيث 8 = ‪c‬‬ ‫2 ‪y‬‬ ‫2 ‪x‬‬ ‫2‬ ‫ومنه تكون معادلة القطع الزائد على الصورة = 2 −‬ ‫1‬ ‫‪a‬‬ ‫‪b‬‬ ‫حيث 8 = 2 ‪a 2 +b 2 =c‬‬ ‫2 = ‪2b = 4 ⇒b‬‬ ‫طول المحور المرافق هو ‪ 2b‬حيث‬ ‫طول المحور القاطع هو ‪ 2a‬حيث 2 = 4− 8 = 2 ‪a = c 2 −b‬‬ ‫2 ‪y‬‬ ‫2 ‪x‬‬ ‫−‬ ‫إذن معادلة القطع الزائد هي : =‬ ‫1‬ ‫4‬ ‫4‬
‫قطع زائد بؤرتاه )0 ,5− ( ,)0 ,5( ورأساه )0 ,3− ( ,)0 ,3(‬ ‫مثال ) 3(‬ ‫1 ( أوجد معادلة القطع الزائد بالصورة القياسية‬ ‫2 ( معادلة كل من الخطين التقاربيين‬ ‫3 ( ارسم المنحنى البياني للقطع الزائد‬ ‫الحل‬ ‫1 ( بما أن البؤرتين وطرفي المحور القاطع ) الرأسين ( تقع على محور السينات‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫2‬ ‫1= 2 −‬ ‫معادلة القطع على الصورة‬ ‫‪a‬‬ ‫‪b‬‬ ‫5= ⇒ )0 ,5(= )0 , ‪(c‬‬ ‫‪c‬‬ ‫3= ⇒ )0 ,3(= )0 , ‪(a‬‬ ‫‪a‬‬ ‫4 = ‪c 2 = a 2 +b 2 ⇒b = c 2 − a 2 = 25 − 9 ⇒b‬‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫−‬ ‫1=‬ ‫معادلة القطع هي :‬ ‫9‬ ‫61‬
‫تابع مثال ) 3(‬ ‫4‬ ‫‪b‬‬ ‫‪y =± x‬‬ ‫±= ‪y‬‬ ‫2( الخطان التقاربيان هما ‪x‬‬ ‫3‬ ‫‪a‬‬ ‫‪y‬‬ ‫)4 ,3−(‬ ‫5‬ ‫)4 ,3(‬ ‫3( رسم القطع الزائد‬ ‫4‬ ‫3‬ ‫- نرسم المستطيل الذي رؤوسه :‬ ‫2‬ ‫1‬ ‫± ± (= ) ± , ± (‬ ‫‪a b‬‬ ‫)4 ,3‬ ‫-3 -4 -5 -6‬ ‫-1 -2‬ ‫1‬ ‫2‬ ‫3‬ ‫4‬ ‫5‬ ‫6‬ ‫‪x‬‬ ‫- نرسم الخطين التقاربيين المائلين :‬ ‫-1‬ ‫-2‬ ‫4‬ ‫±= ‪y‬‬ ‫‪x‬‬ ‫-3‬ ‫3‬ ‫-4‬ ‫)4− ,3− (‬ ‫)4− ,3(‬ ‫-5‬ ‫- نرسم الرسم البياني للقطع الزائد‬
‫تدريبات‬ ‫2 )2 − ‪( y −1) 2 (x‬‬ ‫−‬ ‫1=‬ ‫تدريب ) 1(‬ ‫، أوجد ما يلي :‬ ‫9‬ ‫61‬ ‫قطع زائد معادلته‬ ‫1 ( المركز والرأسين والبؤرتين‬ ‫2 ( معادلة كل من المحور القاطع والمحور المرافق وطول كل منهما‬ ‫3 ( الخطيين التقاربيين‬ ‫تدريب ) 2(‬ ‫هي لقطع زائد ؟‬ ‫هل المعادلة 0 = 4 − ‪y 2 − 4x 2 − 4 y − 8x‬‬ ‫إذا أجبت بنعم ، فما هي الصورة القياسية لمعادلة القطع ؟‬ ‫جد معادلة القطع الزائد الذي مركزه )4− ,2( وإحدى بؤرتيه النقطة )4− ,7(‬ ‫تدريب ) 3(‬ ‫وطول محوره القاطع 8 وحدات .‬
‫الصورة العامة لمعادلة القطوع المخروطية‬ ‫0 = ‪Ax + Bxy + Cy + Dx + Ey + F‬‬ ‫2‬ ‫2‬ ‫المعادلة وشروطها‬ ‫القطع المخروطي‬ ‫0 = ‪ A‬أو 0 = ‪ C‬وليس كليهما‬ ‫ً‬ ‫يكون القطع المكافئ رأسيا‬ ‫يكون القطع المكافئ أفقيا‬ ‫القطع المكافئ‬ ‫إذا كان 0 = ‪C‬‬ ‫إذا كان 0 = ‪A‬‬ ‫0 = ‪A = C − −, − − B‬‬ ‫الدائرة‬ ‫)0 ‪(AC‬‬ ‫إذا كان ‪ A‬و ‪ C‬لهما نفس الاشارة‬ ‫القطع الناقص‬ ‫إذا كان ‪ A‬و ‪ C‬مختلفين بالاشارة )0 ‪(AC‬‬ ‫القطع الزائد‬
‫مثال‬ ‫عين نوع القطع المخروطي الذي معادلته 0 = 731− ‪7 x 2 − 9 y 2 −14x − 54 y‬‬ ‫نّ‬ ‫الحل‬ ‫الصورة العامة لمعادلة القطوع المخروطية هي‬ ‫0 = ‪Ax 2 + Bxy + Cy 2 + Dx + Ey + F‬‬ ‫بمقارنة معادلة القطع المخروطي مع الصورة العامة ، نجد أن :‬ ‫9 = −− = ‪A‬‬ ‫‪7 , C‬‬ ‫−‬ ‫ 36 = × ‪A‬‬ ‫‪C‬‬ ‫−‬ ‫0‬ ‫هي معادلة لقطع زائد‬ ‫إذن المعادلة 0 = 731− ‪7 x 2 − 9 y 2 −14x − 54 y‬‬
‫‪Conics‬‬ ‫القطوع المخروطية‬ ‫‪Focus‬‬ ‫بؤرة‬ ‫‪Directrix‬‬ ‫دليل‬ ‫‪Parabola‬‬ ‫القطع المكافئ‬ ‫‪Parabloid‬‬ ‫سطح مكافئ‬ ‫‪Ellipse‬‬ ‫القطع الناقص‬ ‫‪Hyperbola‬‬ ‫القطع الزائد‬ ‫‪Center‬‬ ‫مركز‬ ‫‪Vertex‬‬ ‫رأس‬ ‫‪Transverse axis‬‬ ‫المحور القاطع‬ ‫‪Conjugate axis‬‬ ‫المحور المرافق‬ ‫‪Asymptotes‬‬ ‫خطوط تقاربية‬
http://mathdemos.gcsu.edu/mathdemos/family_of_func tions/conic_gallery.html http://math2.org/math/algebra/conics.htm http://cs.jsu.edu/~leathrum/Mathlets/conics.html http://www2.krellinst.org/UCES/archive/resources/coni cs/newconics.html http://www.stewartcalculus.com/data/ESSENTIAL %20CALCULUS%20Early %20Transcendentals/upfiles/ess-reviewofconics.pdf
القطوع المخروطية Conicss

More Related Content

PPTX
استراتيجية الفصل المقلوب
byتقنيات التعليم
 
PDF
الأدارة الصفية الفعالة
byرؤية للحقائب التدريبية
 
PPT
ادارة الصف
bysayedmetwaly
 
PDF
الانشطة الواجب تنفيذها بمركز مصادر
bySalem AlMuhajri
 
PDF
ديداكتيك النشاط العلمي
byOstadxyz
 
PPTX
طرق وأساليب تدريس القران الكريم
byد.فداء الشنيقات
 
PPTX
نظريات التعلم واستراتيجيات التدريس و التعليم المبرمج.Pptx
byMunirah Alrowibah
 
DOCX
تصميم درس باستخدام نموذج جيرلاك وايلي ودمج التقنية في الدرس باستخدام نموذج (TIP)
byarwa88
 
استراتيجية الفصل المقلوب
byتقنيات التعليم
 
الأدارة الصفية الفعالة
byرؤية للحقائب التدريبية
 
ادارة الصف
bysayedmetwaly
 
الانشطة الواجب تنفيذها بمركز مصادر
bySalem AlMuhajri
 
ديداكتيك النشاط العلمي
byOstadxyz
 
طرق وأساليب تدريس القران الكريم
byد.فداء الشنيقات
 
نظريات التعلم واستراتيجيات التدريس و التعليم المبرمج.Pptx
byMunirah Alrowibah
 
تصميم درس باستخدام نموذج جيرلاك وايلي ودمج التقنية في الدرس باستخدام نموذج (TIP)
byarwa88
 

What's hot

PPT
التباديل و التوافيق
byng1234567ng
 
PDF
‏‏نماذج دمج التقنية Tpack
byعبدالله يحي
 
PDF
إستراتيجيات التعليم والتعلم الفعالة
byرؤية للحقائب التدريبية
 
PPTX
دورة التفوق الدراسي
byمحمد بن احمد بابا
 
PDF
اللوحات التعليمية ‎(Educational boards)‎
byJawhara Abueita
 
PPTX
استراتيجيات التعليم والتعلم الالكترونية الحديثة
bypinkrose28
 
PPTX
البنائية بوربوينت النظرية في التدريس.pptx
bygamar abuswar
 
PPTX
القوى في بعد واحد
byjawaher basmad
 
PDF
الممارسات التأمُّلية في التدريس
byرؤية للحقائب التدريبية
 
PDF
التخطيط للتدريس ومكوناته
byguest3a24ea
 
PPTX
ورشة عمل المنهج القائم على الكفايات .. د. بدر الفليج
byDr. Bader Alflaij
 
PDF
البحث الاجرائي
byMoh Gaber
 
PPTX
تاريخ الاصلاحات التعليمية بالمغرب.pptx
byAminePeaceMaoukil
 
PPTX
علوم التربية.pptx
byimadnaji
 
PPTX
فضاء المعلمات و المعلمين - المشروع بالقسم التحضيري
byImed Ilahi
 
PPTX
المحاضرة الثالثة تخطيط المخزون.pptx
byDr. Mohammed Emmam
 
PDF
القيادة الحديثة
byMuhammed Rashed
 
PPTX
ديداكتيك-الرياضيات -بنساسي.pptx
byYasminaABIB
 
PPTX
مهارة الادارة الصفية.pptx
byAlbertEinstein573291
 
DOC
النظرية البنائية لبياجية في التعلم المعرفي
byMohamed Saad Gelbana
 
التباديل و التوافيق
byng1234567ng
 
‏‏نماذج دمج التقنية Tpack
byعبدالله يحي
 
إستراتيجيات التعليم والتعلم الفعالة
byرؤية للحقائب التدريبية
 
دورة التفوق الدراسي
byمحمد بن احمد بابا
 
اللوحات التعليمية ‎(Educational boards)‎
byJawhara Abueita
 
استراتيجيات التعليم والتعلم الالكترونية الحديثة
bypinkrose28
 
البنائية بوربوينت النظرية في التدريس.pptx
bygamar abuswar
 
القوى في بعد واحد
byjawaher basmad
 
الممارسات التأمُّلية في التدريس
byرؤية للحقائب التدريبية
 
التخطيط للتدريس ومكوناته
byguest3a24ea
 
ورشة عمل المنهج القائم على الكفايات .. د. بدر الفليج
byDr. Bader Alflaij
 
البحث الاجرائي
byMoh Gaber
 
تاريخ الاصلاحات التعليمية بالمغرب.pptx
byAminePeaceMaoukil
 
علوم التربية.pptx
byimadnaji
 
فضاء المعلمات و المعلمين - المشروع بالقسم التحضيري
byImed Ilahi
 
المحاضرة الثالثة تخطيط المخزون.pptx
byDr. Mohammed Emmam
 
القيادة الحديثة
byMuhammed Rashed
 
ديداكتيك-الرياضيات -بنساسي.pptx
byYasminaABIB
 
مهارة الادارة الصفية.pptx
byAlbertEinstein573291
 
النظرية البنائية لبياجية في التعلم المعرفي
byMohamed Saad Gelbana
 

Viewers also liked

PPTX
القطع المكافئ
byعائشه الجهني
 
PPTX
الصف التاسع رياضيات لبقطع المكافىء
byمحمد عبد اللطيف
 
RTF
X-rays
byHeba RaAfat
 
PPTX
كتيب الهندسة
bynymath
 
PDF
ملزمة الرياضيات السادس العلمي الأحيائي الفصل الرابع التكامل2017 الأستاذ علي حميد
bymoeiraqi.org
 
PPSX
القطع الزائد
bynymath
 
PPSX
القطع الناقص
bynymath
 
PPS
الانتقال والدوران
byguestcb9b63
 
PPTX
Intensifying Screen (x-ray)
byCeljhon Ariño
 
PPT
Intensifying screens & films
byVishwanath R S
 
PDF
Medical x ray image sensors
byIslam Kotb Ismail
 
PPT
Intensifying screens
byEddy Rumhadi
 
PDF
radiology-x-ray film & screens
byParth Thakkar
 
PPT
Digital Radiography
byricksw78
 
PPT
Image quality, digital technology and radiation protection
byRad Tech
 
PPT
X ray tube
byRad Tech
 
PPT
X ray films
byhmdali
 
القطع المكافئ
byعائشه الجهني
 
الصف التاسع رياضيات لبقطع المكافىء
byمحمد عبد اللطيف
 
X-rays
byHeba RaAfat
 
كتيب الهندسة
bynymath
 
ملزمة الرياضيات السادس العلمي الأحيائي الفصل الرابع التكامل2017 الأستاذ علي حميد
bymoeiraqi.org
 
القطع الزائد
bynymath
 
القطع الناقص
bynymath
 
الانتقال والدوران
byguestcb9b63
 
Intensifying Screen (x-ray)
byCeljhon Ariño
 
Intensifying screens & films
byVishwanath R S
 
Medical x ray image sensors
byIslam Kotb Ismail
 
Intensifying screens
byEddy Rumhadi
 
radiology-x-ray film & screens
byParth Thakkar
 
Digital Radiography
byricksw78
 
Image quality, digital technology and radiation protection
byRad Tech
 
X ray tube
byRad Tech
 
X ray films
byhmdali
 

Similar to القطوع المخروطية Conicss

PDF
ملزمة الرياضيات السادس العلمي2017 - القطوع المخروطية
byAhmed Mahdi
 
PDF
1com3mbachir
byaddabenslimmohammed
 
PDF
1com
byaddabenslimmohammed
 
PDF
2010
byblogger
 
PDF
2004rat
byblogger
 
PDF
2011
byblogger
 
PDF
2010rat
byblogger
 
PDF
2009rat
byblogger
 
PDF
2004
byblogger
 
PDF
3 الاتصال
byMohammed Alkadri
 
PDF
أساسيات الرياضيات بأسلوب بسيط -باسم المياحي
byOnline
 
PDF
2012rat
byblogger
 
PPTX
Cours-almalam-fi-almostawa-ppt-3ere-college.pptx
byAmine261388
 
PDF
2008
byblogger
 
DOC
المعادلات
byHassan9999
 
DOC
ملف تاسع ف 1 اوراق العمل
byfatima harazneh
 
PPTX
دوال دورية
byhuda alz
 
PDF
الترتيب
byAHMED ENNAJI
 
PDF
Hhhh
byMohamed Boufettal
 
PDF
مراجعة مركزة -قصي هاشم 2015
byOnline
 
ملزمة الرياضيات السادس العلمي2017 - القطوع المخروطية
byAhmed Mahdi
 
1com3mbachir
byaddabenslimmohammed
 
1com
byaddabenslimmohammed
 
2010
byblogger
 
2004rat
byblogger
 
2011
byblogger
 
2010rat
byblogger
 
2009rat
byblogger
 
2004
byblogger
 
3 الاتصال
byMohammed Alkadri
 
أساسيات الرياضيات بأسلوب بسيط -باسم المياحي
byOnline
 
2012rat
byblogger
 
Cours-almalam-fi-almostawa-ppt-3ere-college.pptx
byAmine261388
 
2008
byblogger
 
المعادلات
byHassan9999
 
ملف تاسع ف 1 اوراق العمل
byfatima harazneh
 
دوال دورية
byhuda alz
 
الترتيب
byAHMED ENNAJI
 
Hhhh
byMohamed Boufettal
 
مراجعة مركزة -قصي هاشم 2015
byOnline
 

القطوع المخروطية Conicss

  • 2.
    ‫القطع المكافئ‬ ‫مقدمة‬ ‫القطع الزائد‬ ‫القطع الناقص‬ ‫مواقع مفيدة‬ ‫مصطلحات رياضية‬
  • 4.
    ‫القطوع المخروطية ‪ConicSections‬‬ ‫إذا قطع مستوى مخروطين‬ ‫قائمين مقلوبين ل نهائيين في‬ ‫أوضاع واتجاهات مختلفة فإننا‬ ‫نحصل على قطوع مختلفة تسمى‬ ‫قطوعا مخروطية .‬ ‫ ً‬
  • 6.
    ‫القطع المكافئ ‪Parabola‬‬ ‫محورالتماثل‬ ‫مجمـــــــوعـة‬ ‫القطـع المكافئ هـو :‬ ‫البؤرة‬ ‫كل النقـــــاط في المستوى‬ ‫المتساويــــة البعدين عن نقطة‬ ‫معطـــاة ومستقيــــم معطى .‬ ‫الرأس‬ ‫الدليل‬ ‫تسمى النقطة بالبؤرة والمستقيم بالدليل‬ ‫يوجد للقطع المكافئ محور تماثل‬
  • 7.
    ‫‪y‬‬ ‫معادلة القطع المكافئ الذي رأسه ) 0 , 0 (‬ ‫0> ‪p‬‬ ‫مفتوح للعلى‬ ‫) ‪A (x , y‬‬ ‫) ‪A (x , y‬‬ ‫وبؤرته ) 0 , ‪ ( p‬ودليله ‪y = - p‬‬ ‫1‬ ‫= ‪y‬‬ ‫‪x‬‬ ‫2‬ ‫المعادلة هي :‬ ‫) ‪(0, p‬‬ ‫‪4p‬‬ ‫‪x‬‬ ‫‪y = −p‬‬ ‫والصورة القياسية هي :‬ ‫‪y‬‬ ‫‪y =−p‬‬ ‫0< ‪p‬‬ ‫‪y = ax‬‬ ‫2‬ ‫‪x‬‬ ‫حيث أن :‬ ‫) ‪(0, p‬‬ ‫1‬ ‫1‬ ‫−= ‪y‬‬ ‫والدليل‬ ‫,0(‬ ‫)‬ ‫البؤرة هي‬ ‫) ‪A (x , y‬‬ ‫‪4a‬‬ ‫‪4a‬‬ ‫مفتوح للسفل‬ ‫توضيح‬
  • 8.
    ‫بفرض أن 0> ‪ p‬وينطبق ذلك عندما تكون 0 < ‪P‬‬ ‫‪:A‬‬ ‫بعد البؤرة عن النقطة‬ ‫) ‪A (x , y‬‬ ‫2 ) ‪= (x − 0) 2 + ( y − p ) 2 = x 2 + ( y − p‬‬ ‫‪y‬‬ ‫بعد النقطة ‪A‬عن الدليل ‪y = - p‬‬ ‫) ‪A (x , y‬‬ ‫| ‪=| y − − p |=| y + p‬‬ ‫) ‪(0, p‬‬ ‫2 ) ‪| y + p |= x 2 + ( y − p‬‬ ‫‪y = −p‬‬ ‫‪x‬‬ ‫2 ) 2 ) ‪| y + p |2 = ( x 2 + ( y − p‬‬ ‫2 ‪y 2 + 2 py + p 2 = x 2 + y 2 − 2 py + p‬‬ ‫2 ‪−− − −−4 py = x‬‬ ‫2 1‬ ‫= ‪ −− − − −y‬مثال ) 1 (‬ ‫‪x‬‬ ‫‪4p‬‬
  • 9.
    ‫أوجد معادلة القطعالمكافئ الذي بؤرته )2− ,0( ودليله 2 = ‪y‬‬ ‫مثال ) 1 (‬ ‫) ‪A (x , y‬‬ ‫الحل‬ ‫1‬ ‫1‬ ‫1−‬ ‫,0( = )2− ,0(‬ ‫= 2 −−⇒ )‬ ‫= ‪⇒a‬‬ ‫‪4a‬‬ ‫‪4a‬‬ ‫8‬ ‫2 1−‬ ‫‪y = ax ⇒ y = x‬‬ ‫2‬ ‫8‬ ‫مثال ) 2 (‬
  • 10.
    ‫أوجد البؤرة والدليلللقطع المكافئ 2 ‪y = 2x‬‬ ‫مثال ) 2(‬ ‫) ‪A (x , y‬‬ ‫الحل‬ ‫2=‪a‬‬ ‫حيث‬ ‫‪y = ax‬‬ ‫2‬ ‫على الصورة‬ ‫‪y = 2x‬‬ ‫2‬ ‫1‬ ‫1‬ ‫1‬ ‫=‬ ‫=‬ ‫8 )2(4 ‪4a‬‬ ‫1‬ ‫1‬ ‫البؤرة هي :‬ ‫,0(‬ ‫) ,0( = )‬ ‫‪4a‬‬ ‫8‬ ‫1‬ ‫1‬ ‫والدليل هو المستقيم :‬ ‫مثال ) 3(‬ ‫−= ‪y‬‬ ‫− = ‪⇒ −y‬‬ ‫‪4a‬‬ ‫8‬
  • 11.
    ‫أوجد في الصورةالقياسية معادلة القطع المكافئ حيث دليله‬ ‫مثال ) 3(‬ ‫هو المستقيم 4− = ‪ y‬وبؤرته )4 ,0(‬ ‫) ‪A (x , y‬‬ ‫الحل‬ ‫وهو مستقيم أفقي والبؤرة تقع إلى العلى‬ ‫الدليل هو 4− = ‪y‬‬ ‫القطع له خط تماثل رأسي ومفتوح إلى العلى‬ ‫1‬ ‫1‬ ‫− = ‪−y‬‬ ‫= ‪= −4 ⇒ −a‬‬ ‫‪4a‬‬ ‫61‬ ‫2 1‬ ‫‪y = ax − ⇒ − y = x‬‬ ‫2‬ ‫61‬
  • 12.
    ‫‪y‬‬ ‫) ‪A (x , y‬‬ ‫معادلة القطع المكافئ الذي رأسه ) 0 , 0 (‬ ‫‪x = −p‬‬ ‫) ‪A (x , y‬‬ ‫وبؤرته ) 0 , ‪ ( p‬ودليله ‪x = - p‬‬ ‫0> ‪p‬‬ ‫)0 , ‪( p‬‬ ‫‪x‬‬ ‫1‬ ‫= ‪x‬‬ ‫‪y‬‬ ‫2‬ ‫المعادلة هي :‬ ‫مفتوح نحو اليمين‬ ‫‪4p‬‬ ‫والصورة القياسية هي :‬ ‫‪y‬‬ ‫مفتوح نحو اليسار‬ ‫‪x = −p‬‬ ‫‪x = ay‬‬ ‫2‬ ‫حيث أن :‬ ‫)0 , ‪( p‬‬ ‫1‬ ‫1‬ ‫−= ‪x‬‬ ‫‪x‬‬ ‫والدليل‬ ‫(‬ ‫)0 ,‬ ‫البؤرة هي‬ ‫0< ‪p‬‬ ‫‪4a‬‬ ‫‪4a‬‬ ‫) ‪A (x , y‬‬ ‫توضيح‬
  • 13.
    ‫بفرض أن 0> ‪ p‬وينطبق ذلك عندما تكون 0 < ‪P‬‬ ‫‪y‬‬ ‫) ‪A (x , y‬‬ ‫‪:A‬‬ ‫بعد البؤرة عن النقطة‬ ‫‪x = −p‬‬ ‫0> ‪p‬‬ ‫) ‪A (x , y‬‬ ‫2 ‪= (x − p ) 2 + ( y − 0) 2 = (x − p )2 + y‬‬ ‫)0 , ‪( p‬‬ ‫‪x‬‬ ‫بعد النقطة ‪A‬عن الدليل ‪y = - p‬‬ ‫مفتوح نحو اليمين‬ ‫| ‪=| x − − p |=| x + p‬‬ ‫=| ‪| x + p‬‬ ‫2 ) ‪y 2 + (x − p‬‬ ‫2 ) 2 ) ‪| x + p |2 = ( y 2 + (x − p‬‬ ‫2 ‪x 2 + 2 px + p 2 = y 2 + x 2 − 2 px + p‬‬ ‫2 ‪−− −−−4 px = y‬‬ ‫1‬ ‫= ‪ −− − − −x‬مثال ) 1 (‬ ‫2‪y‬‬ ‫‪4p‬‬
  • 14.
    ‫1‬ ‫1‬ ‫مثال ) 1 (‬ ‫−= ‪x‬‬ ‫أوجد معادلة القطع المكافئ الذي بؤرته )0 , ( ودليله‬ ‫4‬ ‫4‬ ‫الحل‬ ‫1‬ ‫1‬ ‫1‬ ‫1‬ ‫(‬ ‫− ⇒ )0 , ( = )0 ,‬ ‫1 = ‪= ⇒a‬‬ ‫‪4a‬‬ ‫4‬ ‫4 ‪4a‬‬ ‫‪x = ay‬‬ ‫2‬ ‫‪x = 1y‬‬ ‫2‬ ‫مثال ) 2 (‬ ‫‪x =y‬‬ ‫2‬
  • 15.
    ‫مثال ) 2(‬ ‫‪x = 3y‬‬ ‫2‬ ‫أوجد البؤرة والدليل للقطع المكافئ‬ ‫) ‪A (x , y‬‬ ‫الحل‬ ‫3= ‪a‬‬ ‫حيث‬ ‫‪x = ay‬‬ ‫2‬ ‫على الصورة‬ ‫‪x = 2y‬‬ ‫2‬ ‫1‬ ‫1‬ ‫1‬ ‫=‬ ‫=‬ ‫21 )3(4 ‪4a‬‬ ‫البؤرة هي :‬ ‫1‬ ‫1‬ ‫)0 , ( = )0 , (‬ ‫‪4a‬‬ ‫21‬ ‫والدليل هو المستقيم :‬ ‫1‬ ‫1‬ ‫− = ‪x = − ⇒ −x‬‬ ‫‪4a‬‬ ‫21‬
  • 16.
    ‫إزاحة القطوع المكافئة‪Translations of Parabolas‬‬ ‫‪y‬‬ ‫عندما يجرى إزاحة قطع مكافئ‬ ‫) ‪(h + p , k‬‬ ‫) ‪(h , k‬‬ ‫أو ‪y = ax‬‬ ‫2‬ ‫معادلته ‪x = ay‬‬ ‫2‬ ‫‪k‬‬ ‫) ‪(h , k‬‬ ‫ ً‬ ‫وحدة ورأسيا‬ ‫ ً‬ ‫أفقيا‬ ‫‪k‬‬ ‫‪h‬‬ ‫)0 ,0(‬ ‫) ‪(h + p , k‬‬ ‫‪x‬‬ ‫‪h‬‬ ‫فإن رأس القطـــع المكــافئ يتحرك‬ ‫إلى‬ ‫من‬ ‫) ‪(h , k‬‬ ‫)0 ,0(‬
  • 17.
    ‫الصورة القياسية لمعادلةالقطع المكافئ الذي رأسه ) ‪(h , k‬‬ ‫الصورة القياسية لمعادلة‬ ‫البؤرة ومعادلة الدليل‬ ‫القطع المكافئ‬ ‫1‬ ‫+ ‪(h , k‬‬ ‫)‬ ‫‪4a‬‬ ‫2 ) ‪y − k = a (x − h‬‬ ‫1‬ ‫− ‪y =k‬‬ ‫‪4a‬‬ ‫1‬ ‫+ ‪(h‬‬ ‫) ‪,k‬‬ ‫‪4a‬‬ ‫1‬ ‫2) ‪x − h = a ( y − k‬‬ ‫− ‪x =h‬‬ ‫‪4a‬‬
  • 18.
    ‫أوجد الصورة القياسيةلمعادلة القطع المكافئ الذي رأسه )4 ,3( وبؤرته )4 ,5(‬ ‫مثال ) 1(‬ ‫بما أن الرأس والبؤرة يقعان على خط أفقي ، والبؤرة إلى يمين الرأس‬ ‫الحل‬ ‫يكون القطع المكافئ مفتوحا إلى اليمين وصورة معادلته 2 ) ‪x − h = a ( y − k‬‬ ‫الرأس هو ) ‪( h , k‬‬ ‫4 = ‪( h , k ) = (3, 4) ⇒ h = 3, k‬‬ ‫1‬ ‫+ ‪(h‬‬ ‫البؤرة هي ) ‪, k‬‬ ‫1‬ ‫1‬ ‫‪4a‬‬ ‫+ ‪(h‬‬ ‫+ ⇒ )4 ,5(= ) ‪, k‬‬ ‫3‬ ‫5=‬ ‫‪4a‬‬ ‫‪4a‬‬ ‫1‬ ‫=‪a‬‬ ‫8‬ ‫الصورة القياسية لمعادلة القطع المكافئ هي :‬ ‫1‬ ‫2 )4 − ‪x − 3 = ( y‬‬ ‫8‬
  • 19.
    ‫الصورة العامة لمعادلةالقطع المكافئ‬ ‫الصورة العامة للقطع المكافئ تأخذ إحدى الصورتين :‬ ‫‪y‬‬ ‫* قطع مكافئ رأسي‬ ‫0 ≠ ‪y = ax +bx + c − , − a‬‬ ‫2‬ ‫‪x‬‬ ‫‪y‬‬ ‫* قطع مكافئ أفقي‬ ‫0 ≠ ‪x = ay + by + c − , −a‬‬ ‫2‬ ‫‪x‬‬
  • 20.
    ‫هي لقطع مكافئ؟‬ ‫0 = 6 − ‪x 2 − 4x + 2 y‬‬ ‫هل المعادلة‬ ‫مثال ) 1(‬ ‫إذا كانت كذلك ، فأوجد الرأس والبؤرة والدليل .‬ ‫بما أن المعادلة تربيعية في المتغير ‪x‬‬ ‫الحل‬ ‫نكمل المربع بالنسبة إلى ‪ x‬لنحصل على الصورة القياسية‬ ‫6 + ‪x 2 − 4x + 2 y − 6 = 0 ⇒ x 2 − 4x = −2 y‬‬ ‫2 4−‬ ‫2 4−‬ ‫‪x‬‬ ‫2‬ ‫( + ‪− 4x‬‬ ‫( + 6 + ‪) = −2 y‬‬ ‫01+ ‪) ⇒( x − 2) 2 = −2 y‬‬ ‫2‬ ‫2‬ ‫−‬‫1‬ ‫وهذه المعادلة على الصورة ) ‪( y − k ) = a ( x − h‬‬ ‫2‬ ‫= )5− ‪( y‬‬ ‫2 )2− ‪(x‬‬ ‫2‬ ‫1−‬ ‫= ‪h = 2−, −k = 5, −a‬‬ ‫2‬ ‫1‬ ‫1‬ ‫9‬ ‫+ ‪(h , k‬‬ ‫+ 5 ,2(= )‬ ‫−‬ ‫1‬ ‫) ,2(= )‬ ‫والبؤرة هي :‬ ‫الرأس هو : )5,2(‬ ‫‪4a‬‬ ‫(4‬ ‫)‬ ‫2‬ ‫2‬ ‫1‬ ‫1‬ ‫11‬ ‫− ‪y =k‬‬ ‫− 5=‬ ‫= ‪⇒y‬‬ ‫والدليل هو :‬ ‫‪4a‬‬ ‫−‬ ‫1‬ ‫2‬ ‫(4‬ ‫)‬ ‫2‬
  • 21.
    ‫تدريبات‬ ‫تدريب ) 1(‬ ‫عين الرأس ، والبؤرة ، ومعادلة محور التماثل ومعادلة الدليل للقطع المكافئ‬ ‫نّ‬ ‫)2 − ‪( y + 1) 2 = 4(x‬‬ ‫تدريب ) 2(‬ ‫1= ‪y‬‬ ‫اكتب معادلة القطع المكافئ الذي رأسه النقطة )4− ,2( ومعادلة دليله هي‬ ‫عند النقطة )4 ,1(‬ ‫‪y 2 = 16x‬‬ ‫تدريب ) 3(‬ ‫أوجد معادلة المماس لمنحنى القطع المكافئ‬
  • 23.
    ‫القطع الناقص ‪Ellipse‬‬ ‫القطع الناقص هو :‬ ‫مجموعــــة كل النقـــــاط في‬ ‫2‪F‬‬ ‫المركز‬ ‫1‪F‬‬ ‫المستوى الذي مجموع بعدي‬ ‫1‪F‬‬ ‫2‪F‬‬ ‫2‪d‬‬ ‫1‪d‬‬ ‫كل منهــــــا عن نقطتين‬ ‫ثابتتين يساوي مقدارا ثابتا .‬ ‫ ً‬ ‫ ً‬ ‫تسمى النقطتان الثابتتان بؤرتين 1‪ ، F2 ، F‬وتسمى نقطة منتصف القطعة المستقيمة الواصلة‬ ‫بينهما مركز القطع الناقص . والبعدان اللذان مجموعهما ثابت هما 1 ‪d 2 ، d‬‬
  • 24.
    ‫محاور القطع الناقص‬ ‫‪y‬‬ ‫المحور الكبر :‬ ‫المحور الصغر‬ ‫المحور الكبر‬ ‫هو القطعة المستقيمة المارة‬ ‫بالبـؤرتيـــن وطرفـاهـــا على‬ ‫القطع ويسمى طرفاهـــا رأسي‬ ‫2‪V‬‬ ‫2‪F‬‬ ‫1‪F‬‬ ‫1‪V‬‬ ‫القطع الناقص .‬ ‫‪x‬‬ ‫1‪F‬‬ ‫2‪F‬‬ ‫المحور الصغر :‬ ‫هو القطعة المستقيمة المارة‬ ‫بالمركز والعمودية على‬ ‫المحور الكبر ، ويقع طرفاها‬ ‫على القطع .‬ ‫المحوران الكبر والصغر هما محورا تماثل القطع الناقص‬
  • 25.
    ‫أطوال محاور القطعالناقص‬ ‫‪y‬‬ ‫طول المحور الكبر ‪2a‬‬ ‫1‪d‬‬ ‫2‪d‬‬ ‫طول المحور الصغر ‪2b‬‬ ‫‪2b‬‬ ‫2‪V‬‬ ‫‪2a‬‬ ‫1‪V‬‬ ‫‪O‬‬ ‫‪x‬‬ ‫البعد بين البؤرتين ‪2c‬‬ ‫1‪F‬‬ ‫‪2c‬‬ ‫2‪F‬‬ ‫2 ‪a2 = b 2 + c‬‬ ‫‪d 1 + d 2 = 2a‬‬
  • 26.
    ‫الصورة القياسية لمعادلةالقطع الناقص الذي مركزه )0 ,0(‬ ‫‪y‬‬ ‫) ‪(0, b‬‬ ‫القطع الناقص الفقي‬ ‫)0 , ‪( −a‬‬ ‫2‪F‬‬ ‫1‪F‬‬ ‫)0 , ‪(a‬‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫1= 2 +‬ ‫‪x‬‬ ‫)0 , ‪F1 (−c‬‬ ‫)0 ,0(‬ ‫)0, ‪F2 (c‬‬ ‫المعادلة هي‬ ‫2‬ ‫‪a‬‬ ‫‪b‬‬ ‫) ‪(0, −b‬‬ ‫‪a >b‬‬ ‫حيث :‬ ‫)0 ,− ( ,)0 , ‪(c‬‬ ‫‪c‬‬ ‫البؤرتــــــــــــــان هما‬ ‫)0 ,− ( ,)0 , ‪(a‬‬ ‫‪a‬‬ ‫طرفا المحور الكبر هما‬ ‫طرفا المحور الصغر هما ) − ,0( ,) ‪(0, b‬‬ ‫‪b‬‬
  • 27.
    ‫الصورة القياسية لمعادلةالقطع الناقص الذي مركزه )0 ,0(‬ ‫‪y‬‬ ‫)0 , ‪(a‬‬ ‫القطع الناقص الرأسي‬ ‫) ‪F1(0, c‬‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫2‬ ‫1= 2 +‬ ‫المعادلة هي‬ ‫)0 , ‪(−b‬‬ ‫)0 , ‪(b‬‬ ‫‪b‬‬ ‫‪a‬‬ ‫)0 ,0(‬ ‫‪x‬‬ ‫‪a >b‬‬ ‫حيث :‬ ‫)− ,0( ,) ‪(0, c‬‬ ‫‪c‬‬ ‫البؤرتــــــــــــــان هما‬ ‫) ‪F2 (0, −c‬‬ ‫) ‪(0, −a‬‬ ‫)− ,0( ,) ‪(0, a‬‬ ‫‪a‬‬ ‫طرفا المحور البكبر هما‬ ‫طرفا المحور الغصغر هما )0 ,− ( ,)0 , ‪(b‬‬ ‫‪b‬‬
  • 28.
    ‫مثال‬ ‫أوجد معادلة القطعالناقص الذي بؤرتاه )3− ,0( ، )3,0( وطول المحور‬ ‫الغصغر 4 ، ثم ارسم المنحنى الذي يمثله .‬ ‫‪y‬‬ ‫البؤرتان تقعان على محور الصادات‬ ‫الحل‬ ‫)3,0(‬ ‫3= ‪c‬‬ ‫طول المحور الغصغر يساوي ‪2b‬‬ ‫2 = ‪2b = 4 ⇒ b‬‬ ‫‪x‬‬ ‫2 ‪a 2 = b 2 +c‬‬ ‫31 = 23 + 2 2 = 2 ‪a‬‬ ‫)3− ,0(‬ ‫معادلة القطع الناقص هي :‬ ‫2‪x2 y‬‬ ‫2‪x2 y‬‬ ‫2‬ ‫⇒ 1= 2 +‬ ‫+‬ ‫1=‬ ‫‪b‬‬ ‫‪a‬‬ ‫4‬ ‫31‬
  • 29.
    ‫الصورة القياسية لمعادلةالقطع الناقص الذي مركزه ) ‪(h , k‬‬ ‫‪y‬‬ ‫) ‪(h , k + b‬‬ ‫القطع الناقص الفقي‬ ‫) ‪(h − a, k‬‬ ‫) ‪(h , k‬‬ ‫) ‪(h + a , k‬‬ ‫2 ) ‪(x − h ) 2 ( y − k‬‬ ‫المعادلة هي‬ ‫2‬ ‫+‬ ‫2‬ ‫1=‬ ‫) ‪(h , k − b‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫‪x‬‬ ‫‪a >b‬‬ ‫حيث :‬ ‫البؤرتــــــــــــــان هما ) ‪( h + , k ), ( h − , k‬‬ ‫‪c‬‬ ‫‪c‬‬ ‫طرفا المحور البكبر هما ) ‪(h + a , k ), (h −a , k‬‬ ‫‪c = a −b‬‬ ‫2‬ ‫2‬ ‫2‬ ‫طرفا المحور الغصغر هما ) ‪( h , k +b ), (h , k −b‬‬
  • 30.
    ‫الصورة القياسية لمعادلةالقطع الناقص الذي مركزه ) ‪(h , k‬‬ ‫) ‪(h , k + a‬‬ ‫القطع الناقص الرأسي‬ ‫2 ) ‪(x − h ) 2 ( y − k‬‬ ‫) ‪(h − b , k‬‬ ‫) ‪(h , k‬‬ ‫) ‪(h + b , k‬‬ ‫2‬ ‫+‬ ‫2‬ ‫1=‬ ‫المعادلة هي‬ ‫‪b‬‬ ‫‪a‬‬ ‫‪a >b‬‬ ‫حيث :‬ ‫) ‪(h , k − a‬‬ ‫البؤرتــــــــــــــان هما ) ‪( h , k +c ), ( h , k −c‬‬ ‫طرفا المحور البكبر هما ) ‪( h , k +a ), ( h , k −a‬‬ ‫2 ‪c 2 = a 2 −b‬‬ ‫طرفا المحور الغصغر هما ) ‪( h +b , k ), ( h −b , k‬‬
  • 31.
    ‫مثال ) 1(أوجد الصورة القياسية لمعادلة قطع ناقص طرفي محوره الكبر )1− ,2−( ، )1− ,8(‬ ‫‪Y‬‬ ‫.‬ ‫وطول محوره الغصغر 8‬ ‫الحل‬ ‫‪X‬‬ ‫الشكل المجاور يمثل طرفي المحور الكبر والمحور الغصغر‬ ‫)1− ,3(‬ ‫)1− −(‬ ‫,2‬ ‫− ,8(‬‫)1‬ ‫2) ‪(x − h )2 ( y − k‬‬ ‫2‬ ‫+‬ ‫2‬ ‫غصورة معادلة القطع الناقص هي 1 =‬ ‫‪a‬‬ ‫‪b‬‬ ‫نقطة منتصف المحور الكبر تمثل مركز القطع الناقص‬ ‫1− + 1− 8 + 2−‬ ‫( = ) ‪(h , k‬‬ ‫,‬ ‫)1− ,3( = )‬ ‫2‬ ‫2‬ ‫طول المحور الكبر يساوي ‪2a‬‬ ‫5 = ‪2a = 8 − (−2) = 10 ⇒ a‬‬ ‫طول المحور الغصغر يساوي ‪2b‬‬ ‫4 = ‪2b = 8 ⇒ b‬‬ ‫2 )1− − ‪(x − 3) 2 ( y‬‬ ‫2 )1 + ‪( x − 3) 2 ( y‬‬ ‫معادلة القطع الناقص هي :‬ ‫2‬ ‫+‬ ‫2‬ ‫⇒1 =‬ ‫+‬ ‫1=‬ ‫5‬ ‫4‬ ‫52‬ ‫61‬
  • 32.
    ‫2 )1 +‪(x − 4) 2 ( y‬‬ ‫+‬ ‫1=‬ ‫مثال ) 2( ارسم شكل تقريبيا للقطع الناقص‬ ‫52‬ ‫961‬ ‫من معادلة القطع الناقص نلظحظ أن مركز القطع هو : − ,4(= ) ‪( h , k‬‬ ‫)1‬ ‫الحل‬ ‫ومن المعادلة أيضا نلظحظ أن 961< 52 أي أن المحور الكبر يكون رأسيا‬ ‫ً‬ ‫‪y‬‬ ‫)21,4(‬ ‫31= ⇒ 961= 2 ‪a‬‬ ‫‪a‬‬ ‫)11,4(‬ ‫وهذا يعني أن نقطتي طرفي المحور الكبر تبعدان 31 وظحدة‬ ‫أسفل وأعلى المركز أي عند النقطتين )41− ,4( و )21,4(‬ ‫5= ⇒ 52 = 2 ‪b‬‬ ‫‪b‬‬ ‫‪x‬‬ ‫)1 − ,1 −(‬ ‫)1 − ,9(‬ ‫)1 − ,4(‬ ‫وهذا يعني أن نقطتي طرفي المحور الغصغر تبعدان 5 وظحدات‬ ‫إلى يسار ويمين المركز أي عند النقطتين )1− ,1−( و − ,9(‬ ‫)1‬ ‫)31 − ,4(‬ ‫21 = 52 − 961 = ‪c 2 = a 2 − b 2 ⇒ c‬‬ ‫)41 − ,4(‬ ‫وهذا يعني أن البؤرتان تبعدان 21 وظحدة أسفل‬ ‫وأعلى المركز أي عند النقطتين )31− ,4( و )11,4(‬
  • 33.
    ‫تدريبات‬ ‫أثبت أن المعادلة 0 = 4 − ‪x 2 + 2 y 2 − 4x + 8 y‬‬ ‫تدريب )1(‬ ‫تمثل قطعا ناقصا .‬ ‫ً‬ ‫ً‬ ‫تدريب ) 2(‬ ‫جد معادلة القطع الناقص الذي مركزه )2 ,2( وإظحدى بؤرتيه النقطة )2 ,1−(‬ ‫وطول محوره الكبر 01 2 وظحدة .‬ ‫أوجد معادلة المماس لمنحنى القطع الناقص 8 = 2 ‪ x 2 + y‬عند النقطة )1,2−(‬ ‫تدريب ) 3(‬
  • 35.
    ‫القطع الزائد ‪Hyperbola‬‬ ‫مجموعــــة بكل‬ ‫القطع الزائد هو :‬ ‫النقـــاط في المســــتوى والتــي الفرق‬ ‫المطلق لبعديــن ثابتيـن هو مقدار ثابت‬ ‫ويساوي ‪ 1 −d 2 2a‬‬ ‫‪d‬‬ ‫=‬ ‫2‪F‬‬ ‫‪a‬‬ ‫‪a‬‬ ‫1‪F‬‬ ‫2‪d‬‬ ‫1‪d‬‬ ‫تسمى النقطتان الثابتتان 1‪ F2 ، F‬بؤرتي القطع الزائد‬
  • 36.
    ‫محاور القطع الزائدوخطوطه التقاربية‬ ‫‪y‬‬ ‫يسمى الخطان 1‪L 2 ، L‬‬ ‫المحور المرافق ‪2b‬‬ ‫2‪L‬‬ ‫1‪L‬‬ ‫خطان تقاربيين مائلين‬ ‫) ‪(0, b‬‬ ‫المحور القاطع‬ ‫بؤرة‬ ‫بؤرة‬ ‫القطعة الواغصلة بين الرأسين‬ ‫)0,‪(− a‬‬ ‫)0 ,‪(a‬‬ ‫‪x‬‬ ‫المحور المرافق‬ ‫)0, ‪F2 (−c‬‬ ‫)0 , ‪F1 (c‬‬ ‫هــو القطعة الواغصلة بيـن منتصفي‬ ‫ضلعي المستطيـــــــل الموازييــــن‬ ‫) ‪(0, −b‬‬ ‫للمحور القاطع‬ ‫المحور القاطع ‪2a‬‬ ‫‪c = a +b‬‬ ‫2‬ ‫2‬ ‫2‬
  • 37.
    ‫الصورة القياسية لمعادلةالقطع الزائد الذي مركزه )0 ,0(‬ ‫القطع الزائد الفقي‬ ‫‪y‬‬ ‫‪b‬‬ ‫‪y =− x‬‬ ‫‪b‬‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫‪a‬‬ ‫‪y = x‬‬ ‫‪a‬‬ ‫2‬ ‫1= 2 −‬ ‫المعادلة هي‬ ‫)0 ,0(‬ ‫) ‪(x , y‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫)0 , −(‬ ‫‪c‬‬ ‫)0 , ‪(−a‬‬ ‫)0 , ‪(a , 0) (c‬‬ ‫‪x‬‬ ‫2 ‪c 2 = a2 + b‬‬ ‫حيث :‬ ‫البؤرتـــــــــــان هما )0 , − ( ,)0 , ‪(c‬‬ ‫‪c‬‬ ‫طرفا المحور القاطع )0 , − ( ,)0 , ‪(a‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫الخطان التقاربيان هما : ‪y =± x‬‬ ‫‪a‬‬
  • 38.
    ‫الصورة القياسية لمعادلةالقطع الزائد الذي مركزه )0 ,0(‬ ‫) ‪(x , y‬‬ ‫‪y‬‬ ‫القطع الزائد الرأسي‬ ‫‪a‬‬ ‫)0 , ‪(c‬‬ ‫‪y =− x‬‬ ‫‪b‬‬ ‫‪a‬‬ ‫‪y = x‬‬ ‫2‪y‬‬ ‫2‪x‬‬ ‫‪b‬‬ ‫2‬ ‫1= 2 −‬ ‫المعادلة هي‬ ‫)0 , ‪(a‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫2 ‪c 2 = a2 + b‬‬ ‫حيث :‬ ‫‪x‬‬ ‫البؤرتـــــــــــان هما ) − ,0( ,) ‪(0, c‬‬ ‫‪c‬‬ ‫)0 , ‪(−a‬‬ ‫طرفا المحور القاطع ) − ,0( ,) ‪(0, a‬‬ ‫‪a‬‬ ‫)0 , −(‬ ‫‪c‬‬ ‫‪a‬‬ ‫‪y =± x‬‬ ‫الخطان التقاربيان هما :‬ ‫‪b‬‬
  • 39.
    ‫الصورة القياسية لمعادلةالقطع الزائد الذي مركزه ) ‪(h , k‬‬ ‫‪y‬‬ ‫القطع الزائد الفقي‬ ‫‪b‬‬ ‫) ‪y − k = − (x − h‬‬ ‫‪a‬‬ ‫2) ‪(x − h )2 ( y − k‬‬ ‫2‬ ‫−‬ ‫2‬ ‫1=‬ ‫المعادلة هي‬ ‫) ‪(h − a, k‬‬ ‫) ‪(h + a, k‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫) ‪(h , k‬‬ ‫2 ‪c 2 = a2 +b‬‬ ‫حيث :‬ ‫) ‪(h − c , k‬‬ ‫) ‪(h + c , k‬‬ ‫البؤرتــان هما ) ‪( h +c , k ), ( h −c , k‬‬ ‫‪x‬‬ ‫‪b‬‬ ‫) ‪y − k = (x − h‬‬ ‫طرفا المحور القاطع ) ‪( h +a , k ), ( h −a , k‬‬ ‫‪a‬‬ ‫‪b‬‬ ‫) ‪y − k = ± (x − h‬‬ ‫الخطان التقاربيان هما :‬ ‫‪a‬‬
  • 40.
    ‫الصورة القياسية لمعادلةالقطع الزائد الذي مركزه ) ‪(h , k‬‬ ‫) ‪(x , y‬‬ ‫‪y‬‬ ‫القطع الزائد الرأسي‬ ‫) ‪(h , k + c‬‬ ‫‪a‬‬ ‫) ‪y − k = (x − h‬‬ ‫2) ‪( y − k ) 2 (x − h‬‬ ‫‪b‬‬ ‫2‬ ‫−‬ ‫2‬ ‫1=‬ ‫المعادلة هي‬ ‫‪a‬‬ ‫‪b‬‬ ‫) ‪(h , k + a‬‬ ‫حيث :‬ ‫2 ‪c 2 = a2 + b‬‬ ‫) ‪(h , k‬‬ ‫البؤرتــان هما ) ‪( h , k +c ), ( h , k −c‬‬ ‫) ‪(h , k − a‬‬ ‫‪x‬‬ ‫طرفا المحور القاطع ) ‪( h , k +a ), ( h , k −a‬‬ ‫) ‪(h , k − c‬‬ ‫‪a‬‬ ‫) ‪y − k = − (x − h‬‬ ‫‪b‬‬ ‫‪a‬‬ ‫) ‪y − k = ± (x − h‬‬ ‫الخطان التقاربيان هما :‬ ‫‪b‬‬
  • 41.
    ‫2‬ ‫2‬ ‫مثال ) 1(‬ ‫‪x‬‬ ‫‪y‬‬ ‫−‬ ‫عين بؤرتي وطرفي المحور القاطع وطولي المحورين للقطع الزائد 1 =‬ ‫نّ‬ ‫1‬ ‫4‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫الحل‬ ‫1= 2 −‬ ‫معادلة القطع على الصورة‬ ‫2‪a‬‬ ‫‪b‬‬ ‫2 = ‪a 2 = 4 ⇒a‬‬ ‫إذن‬ ‫1= ‪b 2 =1 ⇒b‬‬ ‫‪c‬‬ ‫نجد قيمة‬ ‫5 = ‪c = a +b ⇒c = a +b = 4 +1 ⇒c‬‬ ‫2‬ ‫2‬ ‫2‬ ‫2‬ ‫2‬ ‫(‬ ‫)0 ,5 − ( ,)0 ,5‬ ‫البؤرتــــان هما )0 , − ( ,)0 , ‪⇐ c‬‬ ‫(‬ ‫‪c‬‬ ‫)0 − ( ,)0 ,2(‬ ‫,2‬ ‫طرفا المحور القاطع )0 , − ( ,)0 , ‪⇐(a‬‬ ‫‪a‬‬ ‫= × = ‪2a‬‬ ‫2 2‬ ‫4‬ ‫⇐‬‫طول المحور القاطع يساوي ‪2a‬‬ ‫= × = ‪2a‬‬ ‫2 2‬ ‫4‬ ‫⇐‬‫طول المحور القاطع يساوي ‪2a‬‬
  • 42.
    ‫مثال ) 2(‬ ‫جد معادلة القطع الزائد الذي طول محوره المرافق 4 ، وبؤرتاه‬ ‫هما النقطتان )8 ± ,0(‬ ‫بما أن البؤرتين هما )8 ± ,0(‬ ‫الحل‬ ‫إذن البؤرتان تقعان على محور الصادات حيث 8 = ‪c‬‬ ‫2 ‪y‬‬ ‫2 ‪x‬‬ ‫2‬ ‫ومنه تكون معادلة القطع الزائد على الصورة = 2 −‬ ‫1‬ ‫‪a‬‬ ‫‪b‬‬ ‫حيث 8 = 2 ‪a 2 +b 2 =c‬‬ ‫2 = ‪2b = 4 ⇒b‬‬ ‫طول المحور المرافق هو ‪ 2b‬حيث‬ ‫طول المحور القاطع هو ‪ 2a‬حيث 2 = 4− 8 = 2 ‪a = c 2 −b‬‬ ‫2 ‪y‬‬ ‫2 ‪x‬‬ ‫−‬ ‫إذن معادلة القطع الزائد هي : =‬ ‫1‬ ‫4‬ ‫4‬
  • 43.
    ‫قطع زائد بؤرتاه)0 ,5− ( ,)0 ,5( ورأساه )0 ,3− ( ,)0 ,3(‬ ‫مثال ) 3(‬ ‫1 ( أوجد معادلة القطع الزائد بالصورة القياسية‬ ‫2 ( معادلة كل من الخطين التقاربيين‬ ‫3 ( ارسم المنحنى البياني للقطع الزائد‬ ‫الحل‬ ‫1 ( بما أن البؤرتين وطرفي المحور القاطع ) الرأسين ( تقع على محور السينات‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫2‬ ‫1= 2 −‬ ‫معادلة القطع على الصورة‬ ‫‪a‬‬ ‫‪b‬‬ ‫5= ⇒ )0 ,5(= )0 , ‪(c‬‬ ‫‪c‬‬ ‫3= ⇒ )0 ,3(= )0 , ‪(a‬‬ ‫‪a‬‬ ‫4 = ‪c 2 = a 2 +b 2 ⇒b = c 2 − a 2 = 25 − 9 ⇒b‬‬ ‫2‪x‬‬ ‫2‪y‬‬ ‫−‬ ‫1=‬ ‫معادلة القطع هي :‬ ‫9‬ ‫61‬
  • 44.
    ‫تابع مثال )3(‬ ‫4‬ ‫‪b‬‬ ‫‪y =± x‬‬ ‫±= ‪y‬‬ ‫2( الخطان التقاربيان هما ‪x‬‬ ‫3‬ ‫‪a‬‬ ‫‪y‬‬ ‫)4 ,3−(‬ ‫5‬ ‫)4 ,3(‬ ‫3( رسم القطع الزائد‬ ‫4‬ ‫3‬ ‫- نرسم المستطيل الذي رؤوسه :‬ ‫2‬ ‫1‬ ‫± ± (= ) ± , ± (‬ ‫‪a b‬‬ ‫)4 ,3‬ ‫-3 -4 -5 -6‬ ‫-1 -2‬ ‫1‬ ‫2‬ ‫3‬ ‫4‬ ‫5‬ ‫6‬ ‫‪x‬‬ ‫- نرسم الخطين التقاربيين المائلين :‬ ‫-1‬ ‫-2‬ ‫4‬ ‫±= ‪y‬‬ ‫‪x‬‬ ‫-3‬ ‫3‬ ‫-4‬ ‫)4− ,3− (‬ ‫)4− ,3(‬ ‫-5‬ ‫- نرسم الرسم البياني للقطع الزائد‬
  • 45.
    ‫تدريبات‬ ‫2 )2 − ‪( y −1) 2 (x‬‬ ‫−‬ ‫1=‬ ‫تدريب ) 1(‬ ‫، أوجد ما يلي :‬ ‫9‬ ‫61‬ ‫قطع زائد معادلته‬ ‫1 ( المركز والرأسين والبؤرتين‬ ‫2 ( معادلة كل من المحور القاطع والمحور المرافق وطول كل منهما‬ ‫3 ( الخطيين التقاربيين‬ ‫تدريب ) 2(‬ ‫هي لقطع زائد ؟‬ ‫هل المعادلة 0 = 4 − ‪y 2 − 4x 2 − 4 y − 8x‬‬ ‫إذا أجبت بنعم ، فما هي الصورة القياسية لمعادلة القطع ؟‬ ‫جد معادلة القطع الزائد الذي مركزه )4− ,2( وإحدى بؤرتيه النقطة )4− ,7(‬ ‫تدريب ) 3(‬ ‫وطول محوره القاطع 8 وحدات .‬
  • 46.
    ‫الصورة العامة لمعادلةالقطوع المخروطية‬ ‫0 = ‪Ax + Bxy + Cy + Dx + Ey + F‬‬ ‫2‬ ‫2‬ ‫المعادلة وشروطها‬ ‫القطع المخروطي‬ ‫0 = ‪ A‬أو 0 = ‪ C‬وليس كليهما‬ ‫ً‬ ‫يكون القطع المكافئ رأسيا‬ ‫يكون القطع المكافئ أفقيا‬ ‫القطع المكافئ‬ ‫إذا كان 0 = ‪C‬‬ ‫إذا كان 0 = ‪A‬‬ ‫0 = ‪A = C − −, − − B‬‬ ‫الدائرة‬ ‫)0 ‪(AC‬‬ ‫إذا كان ‪ A‬و ‪ C‬لهما نفس الاشارة‬ ‫القطع الناقص‬ ‫إذا كان ‪ A‬و ‪ C‬مختلفين بالاشارة )0 ‪(AC‬‬ ‫القطع الزائد‬
  • 47.
    ‫مثال‬ ‫عين نوع القطعالمخروطي الذي معادلته 0 = 731− ‪7 x 2 − 9 y 2 −14x − 54 y‬‬ ‫نّ‬ ‫الحل‬ ‫الصورة العامة لمعادلة القطوع المخروطية هي‬ ‫0 = ‪Ax 2 + Bxy + Cy 2 + Dx + Ey + F‬‬ ‫بمقارنة معادلة القطع المخروطي مع الصورة العامة ، نجد أن :‬ ‫9 = −− = ‪A‬‬ ‫‪7 , C‬‬ ‫−‬ ‫ 36 = × ‪A‬‬ ‫‪C‬‬ ‫−‬ ‫0‬ ‫هي معادلة لقطع زائد‬ ‫إذن المعادلة 0 = 731− ‪7 x 2 − 9 y 2 −14x − 54 y‬‬
  • 48.
    ‫‪Conics‬‬ ‫القطوع المخروطية‬ ‫‪Focus‬‬ ‫بؤرة‬ ‫‪Directrix‬‬ ‫دليل‬ ‫‪Parabola‬‬ ‫القطع المكافئ‬ ‫‪Parabloid‬‬ ‫سطح مكافئ‬ ‫‪Ellipse‬‬ ‫القطع الناقص‬ ‫‪Hyperbola‬‬ ‫القطع الزائد‬ ‫‪Center‬‬ ‫مركز‬ ‫‪Vertex‬‬ ‫رأس‬ ‫‪Transverse axis‬‬ ‫المحور القاطع‬ ‫‪Conjugate axis‬‬ ‫المحور المرافق‬ ‫‪Asymptotes‬‬ ‫خطوط تقاربية‬
  • 49.