يتضمن مجمع الرياضيات للصف التاسع خمس وحدات تغطي مواضيع مثل الهندسة التحليلية والمعادلات والدائرة والتحويلات الهندسية والإحصاء. يُستخدم نموذج تقييم يتضمن امتحانات قبلية وبعدية ومستوى لتقييم تقدم الطلاب ويشمل اختبارات تكوينية ونشاطات تطبيقية. كل وحدة مصممة لمساعدة الطلاب على تحقيق فهم شامل للمواضيع المطلوبة قبل الانتقال إلى الوحدات التالية.









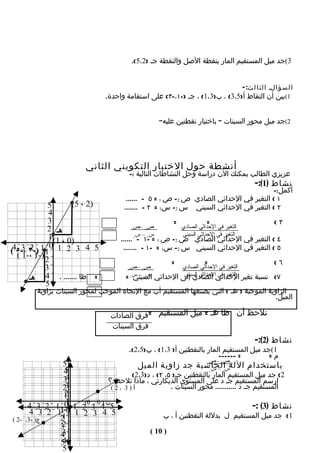
















































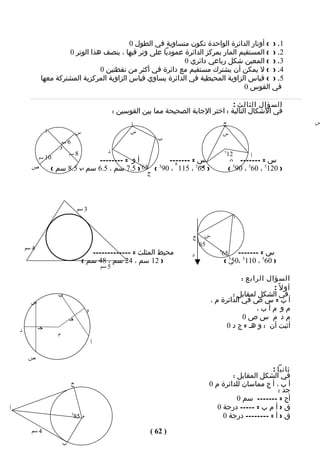
























![4( اختر الجابة الصحيحة :
أ( صورة النقطة ) 2، 3( بالدوران بزاوية 09 درجة عكس عقارب الساعة هي :
] ) 2 ،-3( ، ) -3 ، -2 ( ، ) -3 ، 2 ( ، ) 3 ، 2([
ب( صورة النقطة ) 4، -1( بالدوران بزاوية 09 درجة مع عقارب الساعة هي :
] ) - 1 ،4( ، )4 ، 1 ( ، ) 4 ، -1 ( ، ) -1، -4( [
ج( صورة النقطة ) -5، 3( بالدوران بزاوية 081 درجة هي :
] ) - 3 ،5( ، )-3 ،- 5 ( ، )3 ، -5 ( ، ) 5 ، -3( [
د( انعكاس النقطة )4 ، 2 ( في نقطة الصل يكافئ دورانا :
- بزاوية 09 ْ مع عقارب الساعة
- بزاوية 09 ْعكس عقارب الساعة
- بزاوية 072 ْمع عقارب الساعة
- بزاوية 081 ْ
س 5 ( جد صورة كل شكل مما يلى بالدوران الموضح حول نقطة الصل :
081 ْ 09 ْ عكس عقارب الساعة 09 ْ مع عقارب الساعة
3 3 3
2 2 ب أ
ب 1 أ 1 1
أ
-1 -2 -3 1 2 3 -1 -2 -3 1 2 3 -1 -2 -3 1 2 3
-1 -1 -1
-2 -2 -2
ب
6( لديك المربع أ ب جـ د اكتب رؤوسه بعد دورانه حول مركزه مع عقارب الساعة حسب
المطلوب :
د أ
ج ب
081 ْ 072 ْمع عقارب
09 ْعكس عقارب الساعة
الساعة
) 98 (](https://image.slidesharecdn.com/1-110916095450-phpapp01/85/1-89-320.jpg)



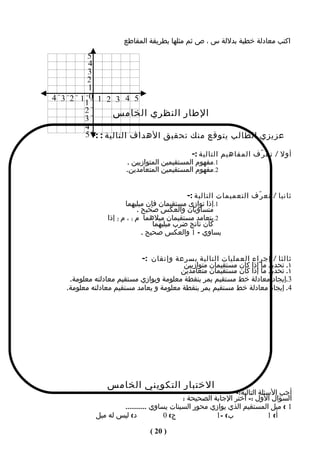
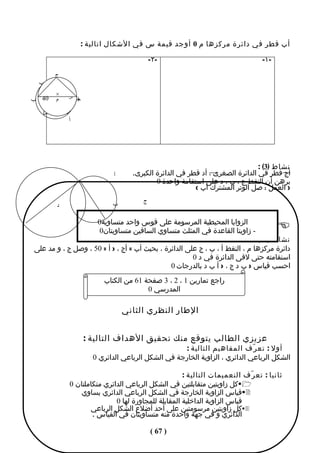
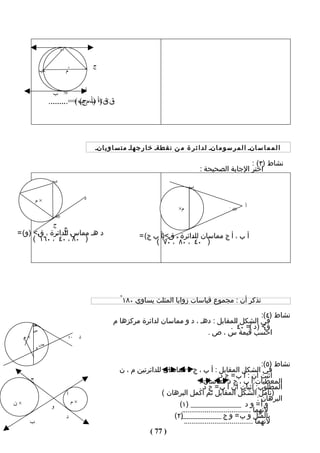
![4( إذا كانت أَ هي صور للنقطة أ عبر عن ذلك بتحويل هندسي مناسب
3
2 أ
×
1
-1 -2 -3 1 2 3
-1 × 5( متى يكون انسحاب نقطة هو نفس النقطة ؟
أ
َ
-2
6( جد صورة المثلث أ ب جـ الذي رؤوسه أ )2 ، 2( ، ب ) 0 ، 3 ( ، جـ ) -1 ، 1( بالنسحاب 3
وحدات باتﺠاه س الموجب .
3
2
1
-1 -2 -3 1 2 3
-1
-2
7( اختر الجابة الصحيحة :
أ( النسحاب يحافظ على :
] الستقامة ، التوازي ، قياس الزوايا ، جميع ما ذكر [
ب( صورة النقطة )2،4( بالنسحاب 4 وحدات بإتﺠاه ص+ هي :
] ) 0 ، 2( ، )6 ، 4( ، )2 ، 8( ، )2 ، -4( [
ج( صورة النقطة ) -1 ، 0 ( بالنسحاب 3 وحدات يمينا هي :
] ) - 4 ، 0( ، )-1 ، 3( ، )2 ، 3( ، )2 ، 0( [
د( صورة النقطة )5 ، -8( بالنسحاب وحدتين باتﺠاه محور السينات السالب هي :
] ) 5 ، -6( ، )5 ،-01( ، )7 ، -8( ، )3 ، -8( [
هـ( صورة النقطة )0 ، -2( بالنسحاب 5 وحدات لسفل هي :
] ) 5 ، -2( ، )0 ، -7( ، )-5 ، -2( ، )0 ، 3( [
8 ( ارسم صورة كل شكل بالنسحاب الموضح :
5 وحدات يمينا وحدتان لعلى 3 وحدات لسفل
) 39 (](https://image.slidesharecdn.com/1-110916095450-phpapp01/85/1-93-320.jpg)







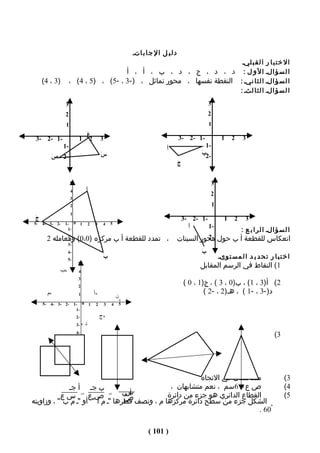








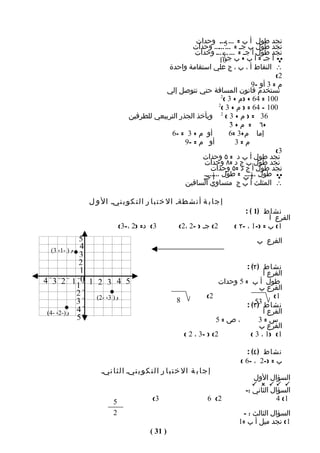
![مربعاته ا - ا ن ح ر ا ف اتـ ك ل ق ي م ة ع ن ا ل و سطـ :
٤ )٣ - ٥ ( = -٢
١ )٤ – ٥ ( = -١
٤ )٧ – ٥ ( = ٢
١ )٦ – ٥ ( = ١
- مجموع المربعات الناتجة = ٤ + ١ + ٤ + ١ = ٠١
- التباين = مجموع هذه المربعات ÷ عددها
= ٠١ ÷ ٤ = ٥.٢
= ٨٥.١ - النحراف المعياري هو الجذر التربيعي للتباين =
5.2
ل حظـ أ ن خ ط و اتـ إ ي ج ا د ا ل ت ب ا ي ن و ا ل ن ح ر افـ ا ل م ع ي ا ريـ م ت ش ا ب هةـ و م ت ر ا ب طةـ
ت د ر يبـ ) ٢( :
جد التباين ثم جد النحراف المعياري للقيم التالية :
أ( ٣ ، ٧ ، ٥
ب( ٢ ، ٤ ، ٦ ، ٧ ، ٨ ، ٩
ن ش اطـ ر ق م ) ٣ ( :
لديك القيم : ٣ ، ٧ ، ٨
- الوسط الحسابي للقيم = )٣٢+٧+٨( ÷ ٣ = ٨١ ÷ ٣ = ٦
٢ ٢
- التباين = [ )٣-٦( + )٧-٦( + )٨-٦( ] ÷ ٣
= ) ٩ + ١ + ٤( ÷ ٣ = ٤١ ÷ ٣ = ٧٦.٤
- النحراف المعياري = 76.4 = ٦١.٢
* ع ن د إ ض ا ف ة ا ل ع د د ٥ ل ك ل ق ي م ة س ا ب ق ة ف إ ن ه ا ت ص بحـ : ٨ ، ٢ ١ ، ٣ ١
الوسط الحسابي بعد التعديل = )٨+٢١+٣١( ÷ ٣ = ١١ -
٢ ٢ ٢
التباين = [ )٨-١١( + )٢١-١١( + )٣١-١١( ] ÷ ٣ -
= ) ٩ + ١ + ٤( ÷ ٣ = ٤١ ÷ ٣ = ٧٦.٤
- النحراف المعياري = 76.4 = ٦١.٢
ه ل ت غ ي رتـ ق ي م ة ا ل ن ح ر افـ ا ل م ع ي ا ريـ ب ع د ا ل ت ع د يلـ ؟ م ا ذ ا ت س ت ن تجـ ؟
* ع ن د ض ربـ ا ل ع د د ٢ ف ي ك ل ق ي م ة ف إ ن ه ا ت ص بحـ : ٦ ، ٤ ١ ، ٦ ١
الوسط الحسابي للقيم = ) ٦+٤١+٦١ ( ÷ ٣٢ = ٢١
٢ ٢ -
التباين = [ )٦-٢١( + )٤١-٢١( + )٦١-٢١( ] ÷ ٣ -
= ) ٦٣ + ٤ + ٦١( ÷ ٣ = ٦٥ ÷ ٣ = ٧٦.٨١
- النحراف المعياري = 76.81 = ٢٣.٤ = ٢ × ٦١.٢
ه ل ت غ ي رتـ ق ي م ة ا ل ن ح ر افـ ا ل م ع ي ا ريـ ب ع د ا ل ت ع د يلـ ؟ م ا ذ ا ت س ت ن تجـ ؟
) 011 (](https://image.slidesharecdn.com/1-110916095450-phpapp01/85/1-110-320.jpg)






