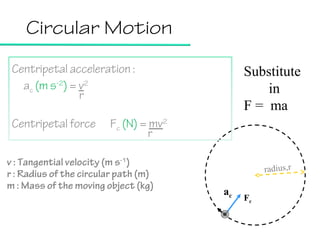
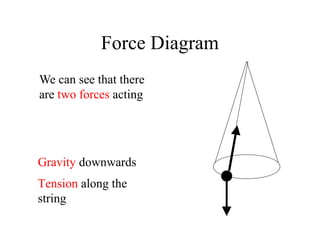
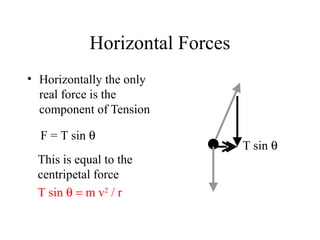
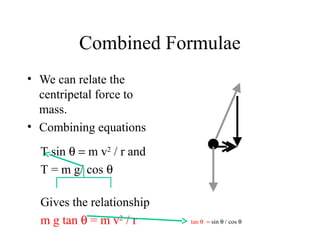
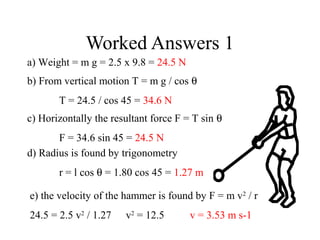
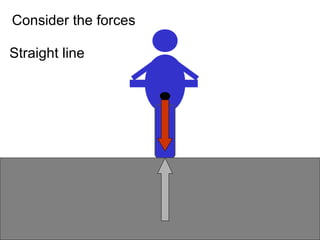
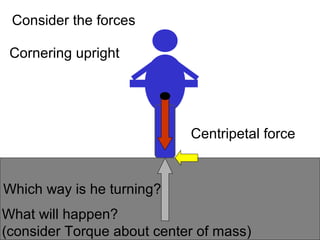
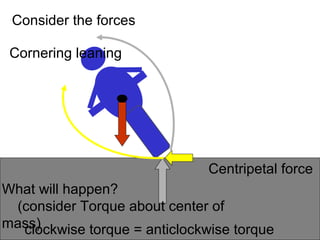
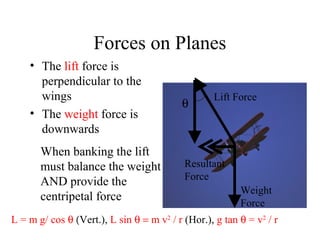
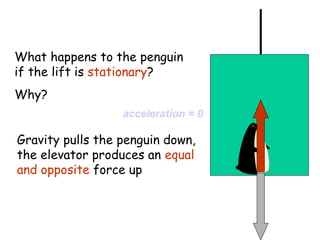
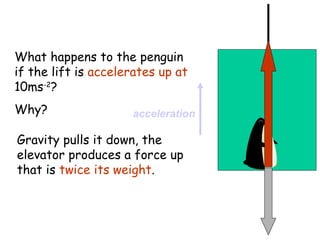
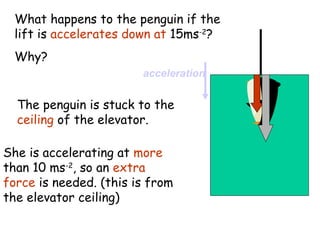
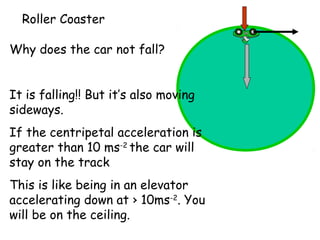
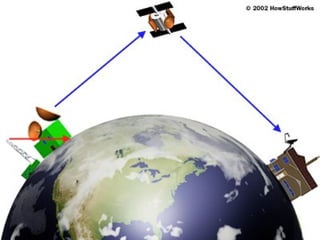
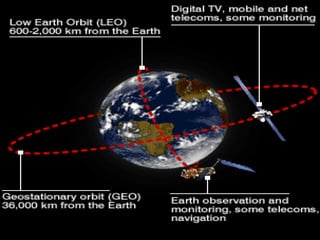
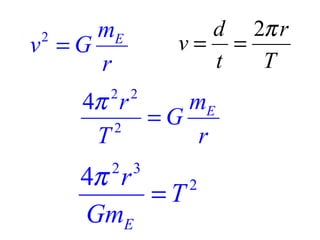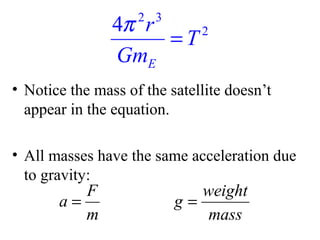This document provides information on circular motion and centripetal force. It defines key terms like centripetal acceleration, centripetal force, and tangential velocity. Formulas are given for centripetal acceleration (a=v2/r), centripetal force (Fc=mv2/r), and tangential velocity (v=2πr/T). Examples of circular motion under combined forces are given, including the conical pendulum, banked curves, and airplanes banking in turns. Vertical circular motion examples like elevators and rollercoasters are also discussed. The document concludes with information on satellite motion and orbits.

1. Circular Motion
The conical pendulum
and beyond

2. Circular motion And Centripetal Force
What you need to know before Circular motion.
1.Force produces acceleration. F = ma(Newton 2)
2.How do I know that an object is accelerating.
What is acceleration?
3.Acceleration causes changing velocity.
4.Distance(d) around a circle is:
•the circumference of a circle
•d = 2πr ( r = radius of a circle)

3. 5.A rotation (or revolution) means once around a
circle.
6.The time to go once around a circle is called the
period (T) of rotation.
7. The number of rotations in one second is the
frequency (f)
8.Frequency is measured in Hertz (hz) or (s -1)
9. We will only be working with CONSTANT
CIRCULAR motion ( v = d/t)
10. What is a tangent???

4. Circular Motion
Definitions
•An object moving at constant speed in a circular path has
the direction of its velocity changing  is accelerating.
•The direction of this acceleration is towards the centre of
the circle.
•The acceleration is perpendicular to the velocity
•This acceleration is called centripetal acceleration.
•The force which produces this acceleration, and therefore
produces the circular motion, is called centripetal force.

5. Circular Motion
• Different forces can provide a centripetal force, e.g. friction
pushing inwards or a rope pulling inwards.
• If the centripetal force is removed then the object will travel at
a tangent to the circle at a constant speed.
Ta
v nge
nti
al
ve
loc
it y
,

6. Circular Motion
Centripetal acceleration :
ac (m s-2) = v2
r
Centripetal force
Substitute
in
F = ma
Fc (N) = mv2
r
v : Tangential velocity (m s-1)
r : Radius of the circular path (m)
m : Mass of the moving object (kg)
radius,r
ac
Fc

7. Circular motion
• When an object undergoes circular motion
it must experience a
centripetal force
• This produces an acceleration
towards the centre of the circle
7

8. Angular
Speed
Centripetal
Force
8

9. 9

10. 10

11. 11

12. Tangential Velocity
• v = d ÷t
• v = circumference ÷ period
• v = 2πr ÷ T
12

13. Acceleration
• The acceleration towards the centre of the
circle is
• a = v2/r
Centripetal Force Equation
•
•
•
•
The general force equation is
F = ma
so the centripetal force equation is
F = mv2/r
13

14. Centripetal Force and acceleration
• Circular motion is accelerated motion as the direction is
changing
• Thus the has to be an unbalanced/net force
• This is the centripetal force
• This centripetal force can come from tension in a string or
friction on a corner etc
• or any other force that pulls inward

15. Friction prevents a 1.5kg mass from falling off a rotating
turntable, which rotates at 30rpm. If the mass is 10cm from the
centre of rotation, what is the friction preventing the mass
moving outwards, and falling off?
Solution:
30 revolutions per minute means 1 revolution takes 2 seconds
T = 2s
r = 0.1m
m = 1.5 kg
v = 2π r ÷ T = 2π x 0.1 ÷ 2 = 0.63/2 = 0.32
F = v2 m
r
= 0.322 X 1.5
0.1
= 1.5 N
Course BOOK page 48 no 1 - 4

16. Conical Pendulum`
• An object swung
slowly on the end of a
string moves in a
circle
But the string is not
horizontal.
The string moves
round in the shape of a
cone

17. Centripetal Force
• Since the object is
moving round in a
circle we know that
there must be a force
towards the centre.
This is called the
centripetal force

18. Force Diagram
We can see that there
are two forces acting
Gravity downwards
Tension along the
string

19. Resultant Force
• With no force acting
towards the centre we
might look at the
resultant force.
The resultant force is
towards the centre
There is no overall
vertical force
component

20. Calculations
• Unfortunately there is
no obvious force
acting to the centre
• So how do the forces
relate to each other,
and to the speed of
circular motion?
• The same basic
formulae apply as
before
• a=v2/r
v=2πr/T
θ
r
v

21. Vertical Forces
• When we consider the
vertical components of
force
• The total is zero
T cos θ
T
θ
So vertical component of
tension = gravity
•T cos θ = m g
•Giving T = m g/ cos θ
W=mg

22. Horizontal Forces
• Horizontally the only
real force is the
component of Tension
F = T sin θ
This is equal to the
centripetal force
T sin θ = m v2 / r
T sin θ

23. Combined Formulae
• We can relate the
centripetal force to
mass.
• Combining equations
T sin θ = m v2 / r and
T = m g/ cos θ
Gives the relationship
m g tan θ = m v2 / r
tan θ = sin θ / cos θ

24. Example 1
Henry is swinging a 2.50 kg hammer round on the end of a 1.80
m long rope.
The angle of the rope to the vertical is 45o.
Calculate:
a) The weight of the hammer (g = 9.8 m s-2)
b) The tension force in the rope
c) The resultant force towards the centre
d) The radius of the circular motion
e) The velocity of the hammer

25. Worked Answers 1
a) Weight = m g = 2.5 x 9.8 = 24.5 N
b) From vertical motion T = m g / cos θ
T = 24.5 / cos 45 = 34.6 N
c) Horizontally the resultant force F = T sin θ
F = 34.6 sin 45 = 24.5 N
d) Radius is found by trigonometry
r = l cos θ = 1.80 cos 45 = 1.27 m
e) the velocity of the hammer is found by F = m v2 / r
24.5 = 2.5 v2 / 1.27
v2 = 12.5
v = 3.53 m s-1

26. Other Circular Motions
• This approach can be
used whenever the
circular motion is
caused by two or more
forces whose resultant
is towards the centre
Cars or bikes on Banked
Curves
Aeroplanes Banking

27. Banked Curves
• We will assume a
Smooth (icy, slippery,
oily, wet) surface.
• i.e. no friction
• Here the two forces
Reaction Force
acting are:
Gravity downwards
Normal Reaction at
θ
90o to the surface
Weight
Force

28. Banked Curve Formulae
• We can relate the
forces in the same way
as with the conical
pendulum
The resultant is towards
the centre (horizontal)
Reaction Force
T = m g/ cos θ (Vertically)
T sin θ = m v2 / r (Horizontally)
θ
Weight
Force
Resultant Force

29. Derivation of Banked Curves
• Divide the x by the y
mv
FN sin θ =
r
FN cosθ = mg
• Gives
2
• Notice mass is not
involved
v2 = rg tan ϴ
v
tan θ =
rg
2

30. Example 2
A motor bike is travelling round a
smooth curve banked at 20o. The
radius of the curve is 55 m. If the
mass of the bike and rider is 275 kg
find the maximum safe speed round
the bend.
How would the maximum safe speed
change if there was friction between
the tyres and the road? Explain your
answer.

31. Worked Answers 2
g tan θ = v2 / r
m = 275 kg, g = 9.8 ms-2, r = 55 m, q = 20o
9.8 tan 20 = v2 / 55
v2 = 196
v = 14 m s-1
With friction the bike can go faster.
This is because the friction force will be down the slope,
stopping the bike sliding off the outside of the track. It will have
a component towards the centre. This will increase the
centripetal force, and hence the maximum speed.

32. Why do motorcyclists lean when
cornering?

33. Consider the forces
Straight line

34. Consider the forces
Cornering upright
Centripetal force
Which way is he turning?
What will happen?
(consider Torque about center of mass)

35. Consider the forces
Cornering leaning
Centripetal force
What will happen?
(consider Torque about center of
mass)
clockwise torque = anticlockwise torque

37. Planes Banking
• With planes it is the
lift force created by
the wings that keeps
the plane flying
In order to turn corners
planes must be tilted, or
banked
A bigger angle of tilt
means a sharper turn
Note banking the plane
causes it to turn

38. Forces on Planes
• The lift force is
perpendicular to the
wings
• The weight force is
downwards
When banking the lift
must balance the weight
AND provide the
centripetal force
θ
Lift Force
Resultant
Force
Weight
Force
L = m g/ cos θ (Vert.), L sin θ = m v2 / r (Hor.), g tan θ = v2 / r

39. Example 3
The picture shows a plane banking. The
plane is travelling at 400 m s-1. By
examining the picture:
a
Estimate the angle of banking.
b
Estimate the mass of the plane.
For your estimates work out:
c
The radius of the circular path
d
The size of the lift force required
by the wings

40. Worked Answers 3
a
Angle is about 25o (20-30)
b
Mass is about 5 tonnes = 5000 kg
c
g tan θ = v2 / r
g = 9.8 m s-2, θ = 25o, v = 400 m s-1
9.8 tan25 = 4002 / r
r = 35000 m = 35 km
L = m g/ cos θ
d
L = 5000 x 9.8 / cos 25 = 54000 N

41. Circular Motion Summary
under the action of two forces
•Real forces may not act towards the centre
•The resultant force always acts towards the centre
•The same basic formulae apply as before a=v2/r
v=2πr/T
•The two forces acting are related by the formulae
T = m g/ cos θ (Vertically)
T sin θ = m v2 / r
(Horizontally)
θ is the angle of tilt to the vertical
•Conical Pendulum, Smooth Banked Curves and Planes Banking
are examples of circular motion caused by two combined forces.

42. Vertical Circular Motion

43. • Why doesn’t he fall at the highest point?

44. What happens to the penguin
if the lift is stationary?
Why?
acceleration = 0
Gravity pulls the penguin down,
the elevator produces an equal
and opposite force up

45. What happens to the penguin
if the lift is accelerates up at
10ms-2?
Why?
acceleration
Gravity pulls it down, the
elevator produces a force up
that is twice its weight.

46. What happens to the penguin
if the lift is accelerates down
at 10ms-2?
Why?
acceleration
The penguin is in freefall.
There is no upward force on
the penguin from the elevator.
When we feel “weight”, it is
the upward force from the
floor. The penguin thinks she
is weightless

47. What happens to the penguin if the
lift is accelerates down at 15ms-2?
Why?
acceleration
The penguin is stuck to the
ceiling of the elevator.
She is accelerating at more
than 10 ms-2, so an extra
force is needed. (this is from
the elevator ceiling)

48. Roller Coaster
Why does the car not fall?
It is falling!! But it’s also moving
sideways.
If the centripetal acceleration is
greater than 10 ms-2 the car will
stay on the track
This is like being in an elevator
accelerating down at › 10ms-2. You
will be on the ceiling.

49. Gravity and Satellites
• How are you able to
watch the All Blacks on
TV when they are
playing in France?
• How are you able to
have a cellphone
conversation with your
friend in the USA?

51. International Space Station

54. Other Uses of Satellites
• Tracking endangered animals

55. Satellite Weather Forecasting

56. Satellites
Satellites are above the atmosphere (no air resistance), so the
only force on them is…………. Gravity

57. Why don’t satellites fall?
• link to Newton's mountain
• Satellites are falling, but they are moving
sideways,
• They fall at the same rate that the earth
curves away under them

59. Weightlessness.
• You don’t feel the gravity force on your
body, you feel the support force pushing up.
• You can feel weightless for two reasons.
1:You are weightless in outer space. There is
no gravity force so there is no reaction force

60. You feel weightless in orbit
• You feel “weight” due to the support force on
you.
• The astronaut and their satellite are in free fall.
• There is no support force acting on them

61. Newton’s Law of Gravitation
m1m2
F =G 2
r

62. Can a satellite have any speed?
• At a certain height, a satellite must have one
particular speed.
• Satellite Speed:
ms mE ms v 2
F =G 2 =
r
r
2
mE v
G 2 =
r
r
mE
2
G
=v
r
mE
v = G
r

63. Period of a satellite
The period of a satellite orbiting around the
earth only depends on the altitude.

64. mE
v =G
r
2
d 2π r
v= =
t
T
mE
4π r
=G
2
T
r
2 2
4π r
2
=T
GmE
2 3

65. 4π r
2
=T
GmE
2 3
• Notice the mass of the satellite doesn’t
appear in the equation.
• All masses have the same acceleration due
to gravity:
F
a=
m
weight
g=
mass

67. • A geostationary satellite has a period of 24 hours
• It must have the earth’s centre as its orbital
centre
• It must be above the equator

68. Geostationary Satellites
AU
S
NZ

69. AU
S
NZ

70. AU
S
NZ

71. AU
S
NZ

72. S
AU
NZ

73. AU
S
NZ

74. AU
S
NZ