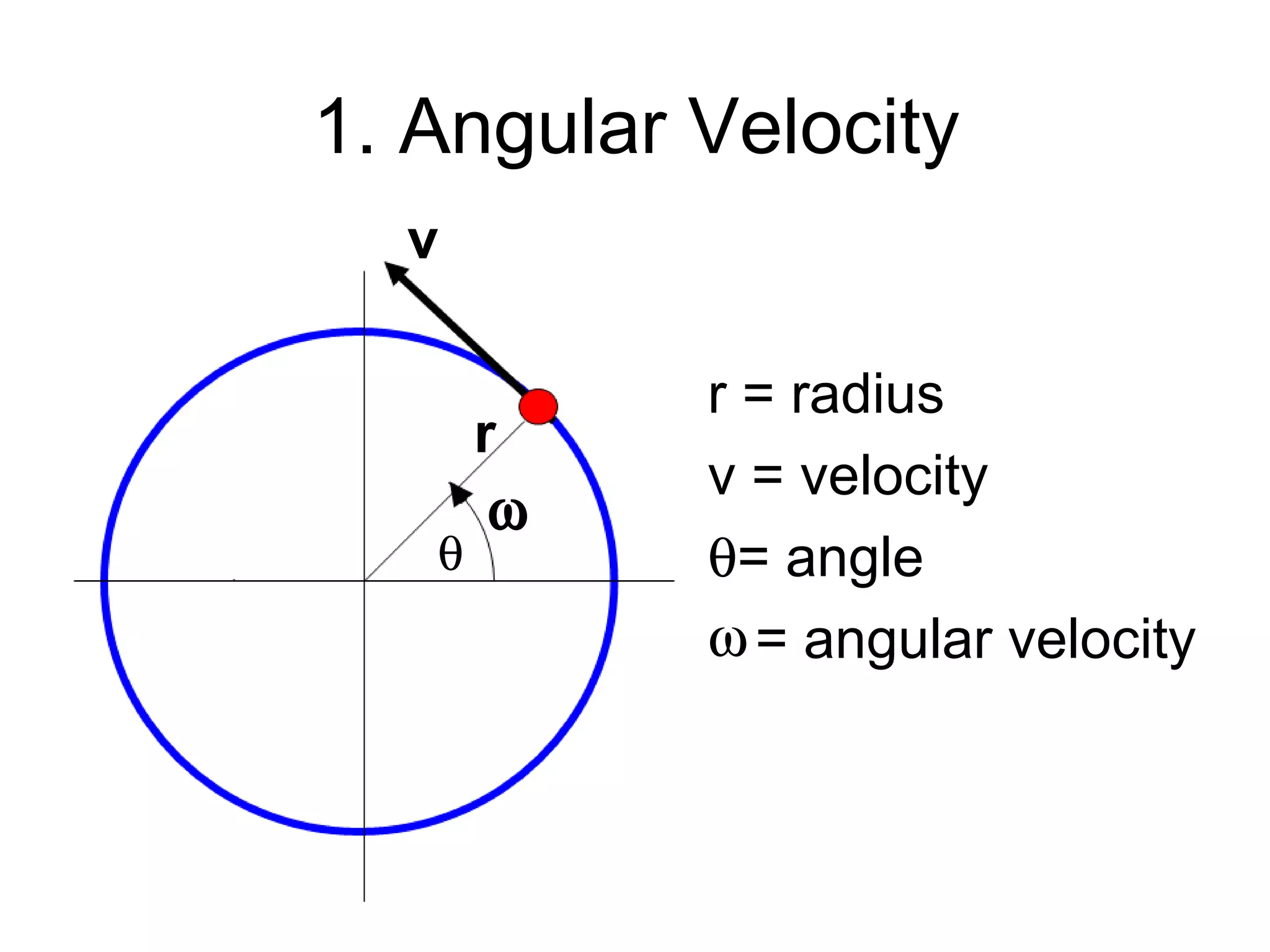
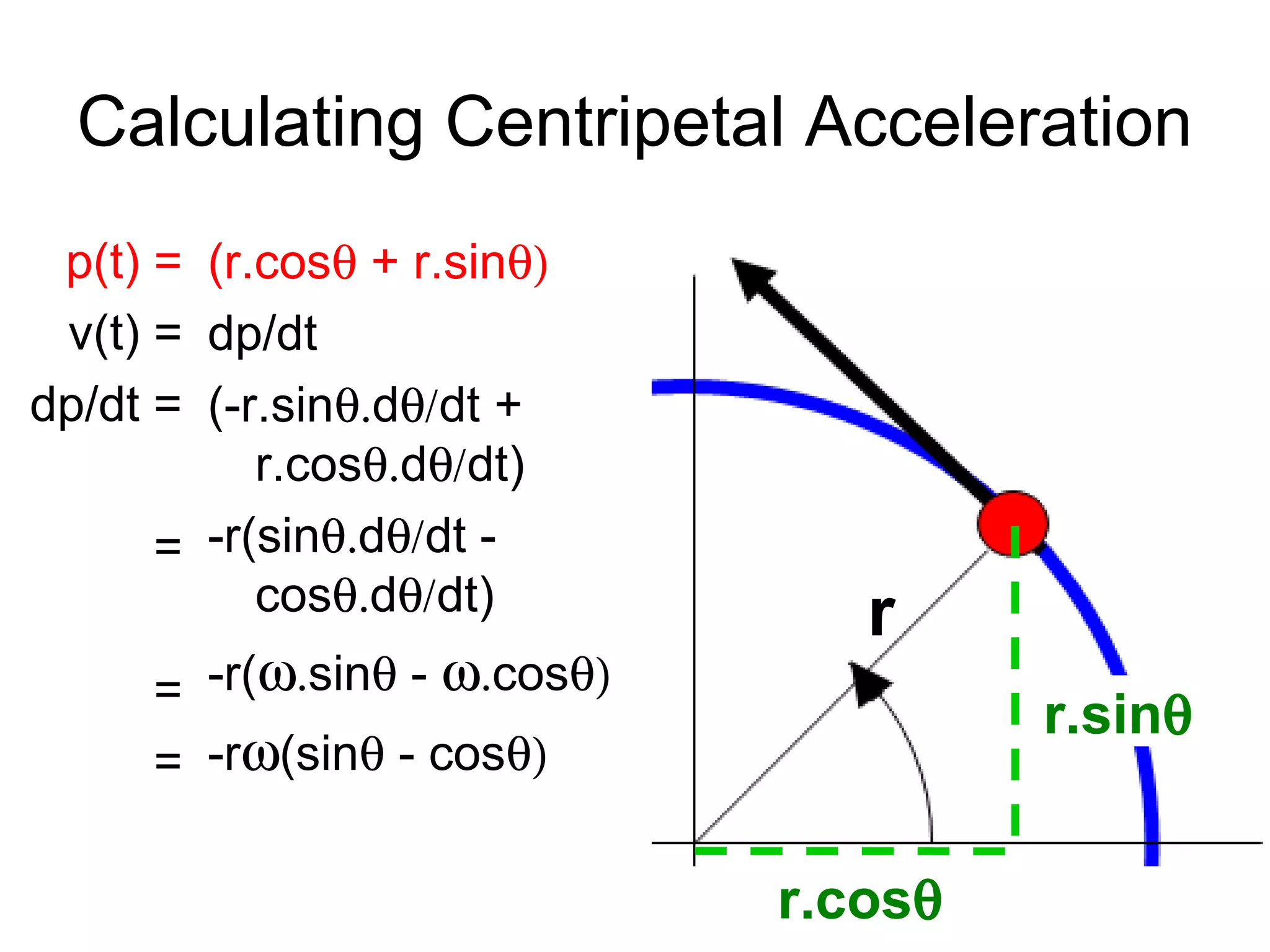
- Uniform circular motion involves constant acceleration towards the center of a circle even when the speed remains constant, because the direction of motion is constantly changing. - This centripetal acceleration is calculated using the angular velocity (ω) and radius (r) as a= v2/r, where v is the velocity. - The centripetal force (F) causing the acceleration is then calculated using F=ma, where m is the mass, giving F=mv2/r. For example, on a motorcycle the centripetal force is provided by friction between the tires and the road.

1. Uniform Circular Motion

2. When a velocity changes, it experiences an
acceleration
Since velocity is a vector, acceleration can be
experienced as …
A change in speed in the same direction
A change in direction at the same speed
A change in both speed and direction

3. • Consider a body travelling in a straight
line:
• Now consider that it changes direction:
• We know from inertia that bodies tend to
travel in a straight line at constant velocity
• If a body changes direction, we know
there must have been a force acting upon
it, and a corresponding acceleration.

4. • A body moving in a circle is constantly
changing direction, and therefore
constantly accelerating.
• In which direction does it accelerate?
• Recall that a = … (vf – vi)/t
Vi
Vf

5. • By subtracting vi from vf …
• … dividing by a scalar: ‘t’
• … and placing the resultant vector between the
initial and final vectors
• … we find that our acceleration points towards
the centre of the circle
• The force which causes this acceleration is
called CENTRIPETAL FORCE
Vf
ViVf – Vi
Vi
Vf

6. This makes sense because when you
consider the forces here …
T

7. … and here
mg

8. What creates the centripetal force
when a motorbike turns?

9. …
or when an
aeroplane
turns?

10. ‘Centrifugal Force’
• It is often easy to believe that some force exists
to pull spinning objects outwards.
• In Newtonian physics, no such force exists
• This apparent ‘force’ is simply the body’s
tendency to continue travelling in a straight line,
disallowed by the constant centripetal force.
• The effect is similar to the feeling of being pulled
to the right when turning left in a car. Of course
you are not being ‘pulled’ to the right, but trying
to continue in your original direction.
• Relativity theory argues that such a centrifugal
force exists from the spinning object’s frame of
reference …
• … but that’s another story

11. Calculating Centripetal Force
In order to calculate centripetal force, we
need to:
1. Understand angular velocity
2. Understand the chain rule in
differentiation
3. Use angular velocity and the chain rule to
calculate centripetal acceleration
4. Use acceleration to calculate centripetal
force.

12. r = radius
v = velocity
θ= angle
ω = angular velocity
θ
v
ω
r
1. Angular Velocity

13. How far will the body travel in
one revolution?
How many radians will the
body travel through in one
revolution?
C = θr
C/t = (θ/t)r
v = ωr
ω = v/r
C = 2πr metres
θ = 2π radians

14. ω = v/r
This implies:
• That larger velocities will produce larger
angular velocities
• And that larger radii will produce smaller
angular velocities
– Eg: a runner on the inside will have an
advantage over a runner on the outside

16. The chain rule
y = f(x)
y’ = f’(x) = dy/dx
Sometimes we don’t have a relationship between y
and x. However, we have relationship between
y and u, and a relationship between u and x.
ie: y = f(u) and u = f(x)
We can can use these to find a relationship
between y and x

17. Using the ‘chain rule’
If:
y = f(u) and u = f(x)
Then:
f’(y) = dy/du and f’(u) = du/dx
And:
dy/dx = …
dy x du
du dx

18. Calculating Centripetal Acceleration
p(t) =
v(t) =
dp/dt =
=
=
=
r
r.cosθ
r.sinθ
(r.cosθ + r.sinθ)
dp/dt
(-r.sinθ.dθ/dt +
r.cosθ.dθ/dt)
-r(sinθ.dθ/dt -
cosθ.dθ/dt)
-r(ω.sinθ - ω.cosθ)
-rω(sinθ - cosθ)

19. Calculating Centripetal Acceleration
v =
a =
dv/dt =
=
=
=
=
r
r.cosθ
r.sinθ
-rω(sinθ - cosθ)
dv/dt
-rω(cosθ.dθ/dt +
sinθ.dθ/dt)
-rω(cosθ.ω+sinθ.ω)
-rω2
(cosθ + sinθ)
-ω2
(r.cosθ + r.sinθ)
-ω2
p

20. Calculating Centripetal Acceleration
a =
IaI =
=
=
r
r.cosθ
r.sinθ
-ω2
p
I-ω2
I.r
(v/r)2
.r
v2
/ r

21. a = v2
/r
This makes sense …
The body will change direction more quickly if:
The velocity is higher
The radius is smaller
For higher velocity, this is easy to imagine
As the radius increases, the circumference
becomes straighter (eg: the horizon) and the
body’s change in direction is very gradual, even
at high speeds.

22. Calculating Centripetal Force
Since: F = ma
And : a = v2
/r
Centripetal force is simply:
F = mv2
/r

23. Angular velocity
θ