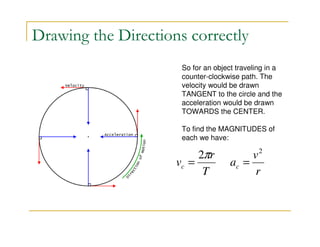
1) Circular motion involves an object moving in a circle with constant speed but changing velocity direction. The velocity is always tangent to the circle while the acceleration points toward the center and is known as centripetal acceleration. 2) Centripetal force provides the necessary centripetal acceleration to cause an object to travel in a circular path and must be present to overcome the object's inertia. This force is proportional to the mass of the object and the square of its velocity. 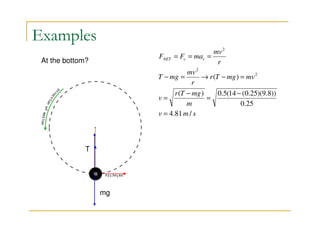3) Examples demonstrate calculating centripetal acceleration and force for objects moving in circular motion, including the minimum coefficient of static friction needed to keep an object rotating on a record and determining the radius of a synchronous satellite orbiting Venus.

1. Circular Motion

2. Speed/Velocity in a Circle
Consider an object moving in a circle
around a specific origin. The DISTANCE the
object covers in ONE REVOLUTION is
called the CIRCUMFERENCE. The TIME
that it takes to cover this distance is called
the PERIOD.
T
r
d
T
scircle
2p
= =
Speed is the MAGNITUDE of the
velocity. And while the speed may be
constant, the VELOCITY is NOT. Since
velocity is a vector with BOTH
magnitude AND direction, we see that
the direction o the velocity is ALWAYS
changing.
We call this velocity, TANGENTIAL velocity as its
direction is draw TANGENT to the circle.

3. Centripetal Acceleration
Suppose we had a circle with angle, q, between 2
radaii. You may recall:
=
s
= arc length in meters
s
r
q
v
v
s
= D
s vt
vt
r
v
v
r
D
=
D
D
q = =
vo
v
Dv
vo v
q
a
v
t
v
r
a centripetal acceleration
c
c
=
=
D
=
2
Centripetal means “center seeking” so that means that the
acceleration points towards the CENTER of the circle

4. Drawing the Directions correctly
So for an object traveling in a
counter-clockwise path. The
velocity would be drawn
TANGENT to the circle and the
acceleration would be drawn
TOWARDS the CENTER.
To find the MAGNITUDES of
each we have:
2 2
v
= =
r
a
p
T
r
vc c

5. Circular Motion and N.S.L
Recall that according to
Newton’s Second Law,
the acceleration is
directly proportional to
the Force. If this is true:
= =
F ma a
NET c
mv
r
F F
v
r
NET c
F Centripetal Force
c
=
= =
2
2
Since the acceleration and the force are directly
related, the force must ALSO point towards the
center. This is called CENTRIPETAL FORCE.
NOTE: The centripetal force is a NET FORCE. It
could be represented by one or more forces. So
NEVER draw it in an F.B.D.

6. Examples
T
r
vc
The blade of a windshield wiper moves
through an angle of 90 degrees in 0.28
seconds. The tip of the blade moves on
the arc of a circle that has a radius of
0.76m. What is the magnitude of the
centripetal acceleration of the tip of the
blade?
2p
2 p
(.76)
= v c = =
4.26 m /
s (.28*4)
2
2 2
23.92 /
(4.26)
ac = = =
0.76
m s
v
r

7. Examples
F F
f c
=
v
rg
mv
2
mv
r
μ
μ
mg
r
F
N
2
2
=
=
=
μ
What is the minimum coefficient of static friction
necessary to allow a penny to rotate along a 33
1/3 rpm record (diameter= 0.300 m), when
the penny is placed at the outer edge of the
record?
Top view
FN
mg
Ff
1min
*
rev rev
=
1.80sec
1sec
= =
2 2 (0.15)
= = =
(0.524)
v
Side view 0.187
(0.15)(9.8)
0.524 /
1.80
0.555
sec
0.555
60sec
min
33.3
2 2
= = =
rg
m s
T
r
v
T
rev rev
c
μ
p p

8. Examples
Venus rotates slowly about its
axis, the period being 243
days. The mass of Venus is
4.87 x 1024 kg. Determine the
radius for a synchronous
satellite in orbit around
Venus. (assume circular
orbit)
Fg
Mm
= =
= =
2 2
mv
= ® = ® =
−
11 24 7 2
(6.67 10 )(4.87 10 )(2.1 10 )
GM
GM
= 3
=
2
3
2
2
2
2
3
2
2
2
2
4
4 4
4
2
p
p p
p
p
x x x
r
GMT
r
GMT
r
T
r
r
T
r
v v
r
r
r
F F G
c
g c
1.54x109 m

9. Examples
The maximum tension that a 0.50
m string can tolerate is 14 N. A
0.25-kg ball attached to this
string is being whirled in a
vertical circle. What is the
maximum speed the ball can
have (a) the top of the circle,
(b)at the bottom of the circle?
T mg
mv
( ) 2
+ = ® + =
( ) 0.5(14 (0.25)(9.8))
r T mg
m
v
v m s
mv
r T mg mv
r
T mg
r
F F maNET c c
5.74 /
0.25
2
2
=
+
=
+
=
= = =

10. Examples
At the bottom?
mv
( ) 2
− = ® − =
( ) 0.5(14 (0.25)(9.8))
r T mg
m
v
v m s
mv
r T mg mv
r
T mg
r
F F maNET c c
4.81 /
0.25
2
2
=
−
=
−
=
= = =
mg
T