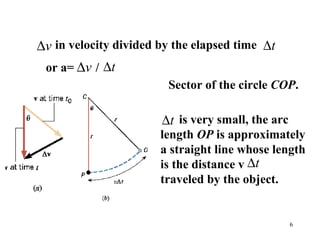
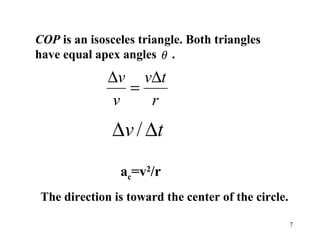
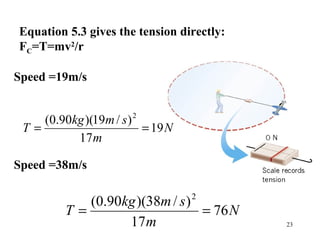
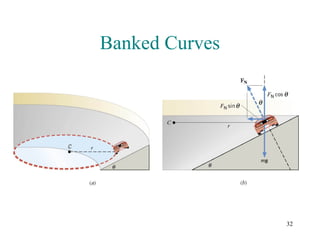
1) Uniform circular motion is motion at a constant speed in a circular path. It requires centripetal acceleration towards the center. 2) The magnitude of centripetal acceleration depends on speed and radius, and is given by a=v^2/r. 3) A centripetal force is needed to produce the centripetal acceleration. This force can be provided by tension (in a rope), friction, or banking of the surface.

1. Uniform
Circular Motion
1
Peter Huruma Mammba
Department of General Studies
DODOMA POLYTECHNIC OF ENERGY AND EARTH RESOURCES
MANAGEMENT (MADINI INSTITUTE) –DODOMA
peter.huruma2011@gmail.com

2. Circular motion
• Is a movement of an object along the
circumference of a circle or rotation along a
circular path.
• It can be uniform with constant speed or
• It can be non-uniform with change in rate of
rotation.
2

3. 3
Uniform Circular Motion
Uniform circular motion is the
motion of an object traveling at a
constant (uniform) speed on a
circular path.
Period T is the time required to
travel once around the circle, that
is, to make one complete
revolution.
v
r
T
π2
=
r

4. 4
Uniform circular motion emphasizes that
1. The speed, or the magnitude of the velocity
vector, is constant.
2. Direction of the vector is not constant.
3. Change in direction, means acceleration
4. “Centripetal acceleration” , it points toward
the center of the circle.

5. 5
Centripetal Acceleration
Magnitude ac of the centripetal acceleration
depends on the speed v of the object and the
radius r of the circular path. ac=v2
/r

6. 6
v∆ in velocity divided by the elapsed time
or a= /
t∆
v∆ t∆
Sector of the circle COP.
is very small, the arc
length OP is approximately
a straight line whose length
is the distance v
traveled by the object.
t∆
t∆

7. 7
COP is an isosceles triangle. Both triangles
have equal apex angles .θ
r
tv
v
v ∆
=
∆
tv ∆∆ /
ac=v2
/r
The direction is toward the center of the circle.

8. 8
Example 1: A Tire-Balancing
Machine
The wheel of a car has a radius of r = 0.29m and is
being rotated at 830 revolutions per minute (rpm)
on a tire-balancing machine. Determine the speed
(in m/s) at which the outer edge of the wheel is
moving.
The speed v can be obtained directly from ,
but first the period T is needed. It must be
expressed in seconds.
T
r
v
π2
=

9. 9
830 revolutions in one minute
revolution
srevolution
min/102.1
min/830
1 3−
×=
T=1.2*10-3
min, which corresponds to 0.072s
sm
s
m
T
r
v /25
072.0
)29.0(22
===
ππ

10. 10
Conceptual Example 2: Which
way will the object go?
An object on a guideline is in
uniform circular motion. The
object is symbolized by a dot,
and at point O it is release
suddenly from its circular
path.
If the guideline is cut suddenly, will the object move along
OA or OP ?

11. 11
Newton’s first law of motion guides our reasoning. An
object continues in a state of rest or in a state of motion
at a constant speed along a straight line unless
compelled to changes that state by a net force. When
the object is suddenly released from its circular path,
there is no longer a net force being applied to the
object. In the case of a model airplane, the guideline
cannot apply a force, since it is cut. Gravity certainly
acts on the plane, but the wings provide a lift force that
balances the weight of the plane.

12. 12
As a result, the object would move along the
straight line between points O and A, not on
the circular arc between points O and P.
In the absence of a net force, then, the plane or
any object would continue to move at a
constant speed along a straight line in the
direction it had at the time of release. This
speed and direction are given in Figure 5.4 by
the velocity vector v.

13. 13
Example 3: The Effect of Radius
on Centripetal Acceleration
The bobsled track at the 1994
Olympics in Lillehammer, Norway,
contained turns with radii of 33 m
and 24 m, as the figure illustrates.
Find the centripetal acceleration at
each turn for a speed of 34 m/s, a
speed that was achieved in the two-
man event. Express the answers as
multiples of g=9.8m/s2
.

14. 14
From ac=v2
/r it follows that
Radius=33m
Radius=24m
gsm
m
sm
ac 6.3/35
33
)/34( 2
2
===
gsm
m
sm
ac 9.4/48
24
)/34( 2
2
===

15. 15
Conceptual Example 4: Uniform
Circular Motion and Equilibrium
A car moves at a constant speed, and there are
three parts to the motion. It moves along a
straight line toward a circular turn, goes
around the turn, and then moves away along a
straight line. In each of three parts, is the car
in equilibrium?

16. 16
An object in equilibrium has no acceleration. As the car
approaches the turn, both the speed and direction of the motion
are constant. Thus, the velocity vector does not change, and
there is no acceleration. The same is true as the car moves away
from the turn. For these parts of the motion, then, the car is in
equilibrium. As the car goes around the turn, however, the
direction of travel changes, so the car has a centripetal
acceleration that is characteristic of uniform circular motion.
Because of this acceleration, the car is not in equilibrium during
the turn.
In general, an object that is in uniform circular
motion can never be in equilibrium.

17. 17
Check your understanding 1
The car in the drawing is moving clockwise around a
circular section of road at a constant speed. What are the
directions of its velocity and acceleration at (a) position 1
and (b) position 2?

18. 18
(a) The velocity is due south, and the
acceleration is due west.
(b) The velocity is due west, and the
acceleration is due north.

19. 19
Centripetal Force

20. 20
Concepts at a glance: Newton’s second law indicates
that whenever an object accelerates, there must be a
net force to create the acceleration. Thus, in uniform
circular motion there must be a net force to produce
the centripetal acceleration. As the Concept-at-a-
glance chart, the second law gives this net force as the
product of the object’s mass m and its acceleration
v2
/r. This chart is an expanded version of the chart
shown previously in Figure 4.9. The net force causing
the centripetal acceleration is called the centripetal
force FC and points in the same direction as the
acceleration- that is, toward the center of the circle.

21. 21
r
mv
FC
2
=
“centripetal force” does not denote a new and
separate force created by nature.

22. 22
Example 5: The Effect of Speed on
Centripetal Force
The model airplane has a mass of 0.90 kg and moves at
a constant speed on a circle that is parallel to the
ground. The path of the airplane and its guideline lie in
the same horizontal plane, because the weight of the
plane is balanced by the lift generated by its wings.
Find the tension T in the guideline(length=17m) for
speeds of 19 and 38m/s.

23. 23
Equation 5.3 gives the tension directly:
FC=T=mv2
/r
Speed =19m/s
Speed =38m/s
N
m
smkg
T 19
17
)/19)(90.0( 2
==
N
m
smkg
T 76
17
)/38)(90.0( 2
==

24. 24
Conceptual Example 6: A Trapeze
Act
In a circus, a man hangs
upside down from a trapeze,
legs bent over the bar and
arms downward, holding his
partner. Is it harder for the
man to hold his partner
when the partner hangs
straight down and is
stationary or when the
partner is swinging through
the straight-down position?

25. 25
Reasoning and Solution: When the man and his
partner are stationary, the man’s arms must
support his partner’s weight. When the two are
swinging, however, the man’s arms must do an
additional job. Then the partner is moving on a
circular arc and has a centripetal acceleration. The
man’s arms must exert and additional pull so that
there will be sufficient centripetal force to produce
this acceleration.
Because of the additional pull, it is harder for the
man to hold his partner while swinging than while
stationary.

26. 26
Example 7: Centripetal Force and
Safe Driving
9.0=− drySµ
Compare the maximum
speeds at which a car can
safely negotiate an
unbanked turn (r= 50.0m)
Sµ
Sµ --dry = 0.9
--icy = 0.1
FS
FS
N
mg
Nf s
s
µ=max

27. 27
NS
MAX
s Ff µ=
The car does not accelerate ,
FN – mg = 0 FN = mg.
r
v
gs
2
=µ grv sµ=∴
fS
N
mg

28. 28
Dry road ( =0.900)sµ
smmsmv /0.21)0.50)(/80.9)(900.0( 2
==
Icy road ( =0.100)sµ
smmsmv /00.7)0.50)(/80.9)(100.0( 2
==
As expected, the dry road allows the greater
maximum speed.

29. 29
Upward on the wing surfaces with a net lifting force L, the
plane is banked at an angle , a component L sin of the
lifting force is directed toward the center of the turn.
θ θ
Greater speeds and/or tighter turns require greater
centripetal forces. Banking into a turn also has an application
in the construction of high-speed roadways.

30. 30
Check your understanding 2
A car is traveling in uniform circular motion on a
section of road whose radius is r. The road is
slippery, and the car is just on the verge of sliding.
(a)If the car’s speed was doubled, what would have
to be the smallest radius in order that the car does
not slide? Express your answer in terms of r.
(b)What would be your answer to part (a) if the car
were replaced by one that weighted twice as
much?

31. 31
(a) 4r (b) 4r

32. 32
Banked Curves

33. 33
A car is going around a friction-free banked
curve. The radius of the curve is r.
FN sin that points toward the center Cθ
r
mv
FF NC
2
sin == θ
FN cos and, since the car does not accelerate in the
vertical direction, this component must balance the
weight mg of the car.
θ
mgFN =θcos

34. 34
mg
rmv
F
F
N
N /
cos
sin 2
=
θ
θ
rg
v2
tan =θ
At a speed that is too small for a given , a car
would slide down a frictionless banked curve: at
a speed that is too large, a car would slide off the
top.
θ

35. 35
Example 8:The Daytona 500
The Daytona 500 is the major event of the
NASCAR (National Association for Stock Car
Auto Racing) season. It is held at the Daytona
International Speedway in Daytona, Florida. The
turns in this oval track have a maximum
radius(at the top)of r=316m and are banked
steeply, with . Suppose these maximum-
radius turns were frictionless. At what speed
would the cars have to travel around them?
°= 31θ

36. 36
From Equation 5.4, it follows that
Drivers actually negotiate the turns at speeds up to
195 mph, however, which requires a greater
centripetal force than that implied by Equation 5.4
for frictionless turns.
smsmmrgv /4331tan)/80.9)(316(tan 2
=°== θ
(96 mph)

37. 37
Check your understanding 4
The acceleration due to gravity on the moon is one-
sixth that on earth.
(a)Is the true weight of a person on the moon less
than, greater than, or equal to the true weight of
the same person on the earth?
(b)Is the apparent weight of a person in orbit about
the moon less than, greater than, or equal to the
apparent weight of the same person in orbit about
the earth?
(a) Less than (b) Equal to

38. 38
Vertical Circular Motion
Usually, the speed varies in this stunt.
“non-uniform”

39. 39
r
mv
mgFN
2
1
1 =−
=FC1
(1)
r
mv
FN
2
2
2 =
=FC2
(2)
=FC3
r
mv
mgFN
2
3
3 =+(3)
r
mv
FN
2
4
4 =
=FC4
(4)
The magnitude of the normal force changes, because
the speed changes and the weight does not have the
same effect at every point.

40. 40
The weight is tangent to the circle at points 2
and 4 and has no component pointing toward
the center. If the speed at each of the four
places is known, along with the mass and
radius, the normal forces can be determined.
They must have at least a minimum speed at the
top of the circle to remain on the track. v3 is a
minimum when FN3 is zero. rgv =3
Weight mg provides all the centripetal force.
The rider experiences an apparent
weightlessness.

41. 41
Concepts & Calculation
Examples 15: Acceleration
At time t=0 s, automobile A is
traveling at a speed of 18 m/s along
a straight road and its picking up
speed with an acceleration that has
a magnitude of 3.5 m/s2
.
At time t=0 s, automobile A is
traveling at a speed of 18 m/s in
uniform circular motion as it
negotiates a turn. It has a
centripetal acceleration whose
magnitude is also 3.5 m/s2
.
Determine the speed of each
automobile when t=2.0 s.

42. 42
Which automobile has a constant acceleration?
Both its magnitude and direction must be constant.
A has constant acceleration, a constant magnitude of 3.5
m/s2
and its direction always points forward along the
straight road.
B has an acceleration with a constant magnitude of 3.5
m/s2
, a centripetal acceleration, which points toward the
center of the circle at every instant.
Which automobile do the equations of kinematics
apply?
Apply for automobile A.

43. 43
Speed of automobile A at t=2.0 s
v=v0+at=18 m/s+(3.5 m/s2
)(2.0 s)=25 m/s
B is in uniform circular motion and goes
around the turn. At a time of t=2.0 s, its speed
is the same as it was at t=0 s, i.e., v=18 m/s.

44. 44
Concepts & Calculation Example
16: Centripetal Force
Ball A is attached to one end of a
rigid mass-less rod, while an
identical ball B is attached to the
center of the rod. Each ball has a
mass of m=0.50kg, and the length
of each half of the rod is L=0.40m.
This arrangement is held by the
empty end and is whirled around
in a horizontal circle at a constant
rate, so each ball is in uniform
circular motion. Ball A travels at a
constant speed of vA=5.0m/s. Find
the tension in each half of the rod.

45. 45
How many tension forces contribute to the centripetal
force that acts on ball A?
A single tension force of magnitude TA acts on ball A,
due to the tension in the rod between the two balls. This
force alone provides the centripetal force keeping ball
A on its circular path of radius 2L
How many tension forces contribute to the centripetal
force that acts on ball B?
Two tension forces act on ball B. TB-TA
Is the speed of ball B the same as the speed of ball A?
No, it is not. Because A travels farther than B in the same
time. A travels a distance equal to the circumference of its
path, which is (2L). B is only L . Speed of ball B is
one half the speed of ball A , or vB=2.5 m/s
π2 π2

46. 46
Ball A Ball B
L
mv
T A
A
2
2
=
L
mv
TT B
AB
2
=−
Centripetal force FC
Centripetal force FC
N
m
smkg
L
mv
T A
A 16
)40.0(2
)/0.5)(50.0(
2
22
===
)40.0(2
)/0.5)(50.0(
40.0
)/5.2)(50.0(
2
2222
m
smkg
m
smkg
L
mv
L
mv
T AB
B +=+=
=23N

47. 47
Problem 4
R = 3.6m
θ = 25
OA = ?

48. 48
Problem 4
REASONING AND SOLUTION Since the speed
of the object on and off the circle remains constant
at the same value, the object always travels the
same distance in equal time intervals, both on and
off the circle. Furthermore since the object travels
the distance OA in the same time it would have
moved from O to P on the circle, we know that the
distance OA is equal to the distance along the arc
of the circle from O to P.

49. 49
Circumference =
and, from the argument given above, we conclude that the
distance OA is 1.6m.
2 2π πr = (3.6 m) = 22.6 m
360o
22.6m
1o
(22.6/360)m
25o
(22.6/360)*25m

50. 50
Problem 43
REASONING In Example 3, it was shown that the
magnitudes of the centripetal acceleration for the
two cases are
Radius 33 m / sC
2
= =a 35 m
Radius 24 m m / sC
2
= =a 48
According to Newton's second law, the centripetal
force is (see Equation 5.3).F maC C
=

51. 51
SOLUTION
a. Therefore, when the sled undergoes the turn of
radius 33 m,
F maC C
2
350 kg)(35 m / s 1.2= = = ×( ) 104
N
b. Similarly, when the radius of the turn is 24 m,
F maC C
2
350 kg)(48 m / s 1.7= = = ×( ) 104
N

52. 52
Problem 46
REASONING AND SOLUTION The force
P supplied by the man will be largest when
the partner is at the lowest point in the
swing. The diagram at the right shows the
forces acting on the partner in this
situation. The centripetal force necessary
to keep the partner swinging along the arc
of a circle is provided by the resultant of
the force supplied by the man and the
weight of the partner.
mg
P

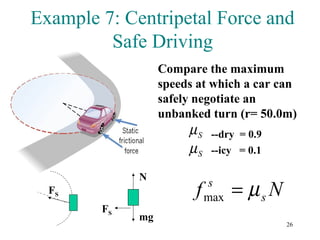
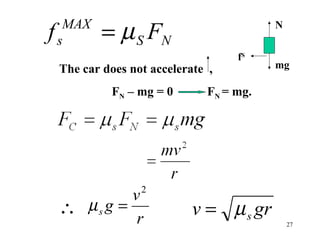
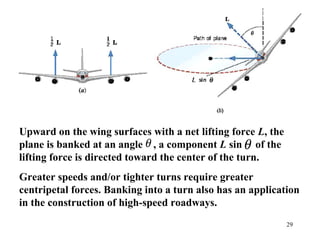
53. 53
P mg
mv
r
− =
2
From the figure
P
mv
r
mg= +
2
Therefore
Since the weight of the partner, W, is equal to mg, it
follows that m = (W/g) and
2 2 2
( / ) [(475 N)/(9.80 m/s )] (4.00 m/s)
(475 N) = 594 N
(6.50 m)
W g v
P W
r
= + = +

54. Assignment 1
• A small ball of mass m is suspended from
a string of length L. The ball revolves with
constant speed v in a horizontal circle of
radius r. (Because the string sweeps out
the surface of a cone, the system is known
as a conical pendulum.) Find an expression
for v. 54

55. Assignment 2
• A civil engineer wishes to redesign the curved
roadway in such a way that a car will not have
to rely on friction to round the curve without
skidding. In other words, a car moving at the
designated speed can negotiate the curve even
when the road is covered with ice.
55

56. Assignment 2 …
Such a road is usually banked, which means
that the roadway is tilted toward the inside
of the curve. Suppose the designated speed
for the road is to be 13.4 m/s (30.0 mi/h) and
the radius of the curve is 35.0 m. At what
angle should the curve be banked?
56