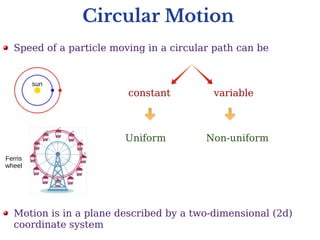
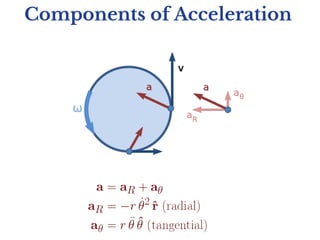
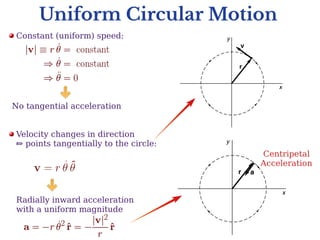
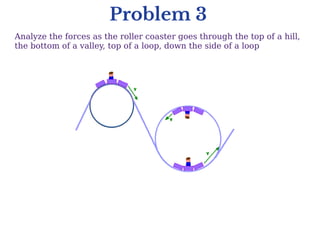
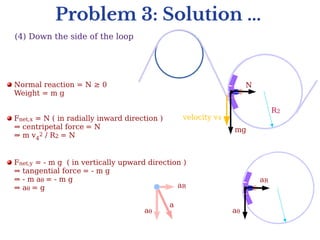
This document discusses uniform and non-uniform circular motion. Uniform circular motion refers to circular motion with constant speed, where the only acceleration is radial inward. Non-uniform circular motion has variable speed, resulting in both radial and tangential acceleration components. Examples are given of both types of motion, including rolling coasters and planets orbiting. Problems analyze the forces involved in different circular motion scenarios like swinging a ball on a string or driving in a banked turn.

1. Uniform & Non-Uniform Circular Motion
Uniform & Non-Uniform Circular Motion
I P S I T A M A N D A L

2. References
An Introduction To Mechanics
by Daniel Kleppner & Robert Kolenkow,
Chapter 1 (sections 1.8, 1.12, 1.13, 1.14)
Fundamentals of Physics
by Jearl Walker, David Halliday, & Robert Resnick,
Chapter 4 (section 4-5)
Introduction to Classical Mechanics
by David Morin, Chapter 3 (section 3.5)

3. Circular Motion
Speed of a particle moving in a circular path can be
constant variable
Uniform Non-uniform
Motion is in a plane described by a two-dimensional (2d)
coordinate system
sun
Ferris
wheel

4. Polar Coordinates ...
Recall ( flipped class lecture at home ):
Directions of unit vectors vary with position
We derived
1
.
ˆ
i
ˆ
j
θ
θ̂
ˆ
r

5. Derivatives of Unit Vectors
Exercise / Tutorial:
Geometric Derivation

6. Velocity
Position:
Velocity:

7. Components of Velocity
Radial Velocity Tangential Velocity
(constant radius)

8. Change in Velocity
Velocity is a vector ⤇ has (1) magnitude (speed), (2) direction
A change in velocity results in acceleration ⤇ a net force acts on the
body
The change may involve magnitude and / or direction ⤇ a body in
circular motion ( ) is accelerating
= change in velocity

9. Clicker Question
According to Newton’s laws, in an inertial frame, what is the net force
acting on a body in a circular motion ?
A: Zero
B: Non-zero
C: Can be zero or non-zero depending on whether speed is constant or
changing

10. Acceleration
Radial Acceleration Tangential Acceleration
(constant radius)

11. Components of Acceleration

12. Constant
Angular Speed

13. Uniform Circular Motion
Constant (uniform) speed:
No tangential acceleration
Velocity changes in direction
⤇ points tangentially to the circle:
Radially inward acceleration
with a uniform magnitude
Centripetal
Acceleration

14. Centripetal acceleration arises from a centripetal force:
Centripetal force accelerates a body by changing the direction of
its velocity without changing its speed
Centripetal Force

15. Period T of uniform circular motion = time for one revolution
(one complete trip around the circle)
Period of Motion
Distance = Speed x Time
⇒ Circumference of the circle = v T
⇒ 2 π r = v T
⇒ T = 2 π r / v

16. Examples
Swinging a ball on the end of a string ⤇ tension provides the
centripetal force
Satellite in a circular orbit around Earth
⤇ gravity provides the centripetal force

17. Examples ...
Car moving in a horizontal circle on a level surface ⤇ friction provides
the centripetal force
Death spiral in figure skating ⤇ the man is the center of rotation (one
toe dug into the ice in a pivot position), exerting centripetal force to
keep his partner moving in a circle

18. Problem 1
A bob of mass m hangs from a string of length L. Conditions have been
set up so that the mass swings around in a horizontal circle, with the
string making an angle of ϕ with the vertical. What is the angular
speed ω of the bob?
R = L sin ϕ
ϕ
L
R
m
Weight = m g
Tension = T
ϕ

19. Problem 1 ...
ϕ
T
T cos ϕ
T sin ϕ
a = v2 / R
m g
Bob
0 = T cos ϕ - m g ( y-direction )
- m a = - T sin ϕ ( r-direction )
gives
a / g = tan ϕ
⇒ v2 = R g tan ϕ
⇒ R2 ω2 = R g tan ϕ
⇒ ω2 = g tan ϕ / ( L sin ϕ)

20. Problem 2
A car of mass m moves at a constant speed v around a banked circular
track of radius R . If the friction is negligible (slippery conditions like ice
on a highway or oil on a racetrack), what bank angle φ prevents sliding?
φ
v
φ
φ
Weight = m g
Normal reaction = N
φ
N
N cos φ
N sin φ
a = v2 / R
m g
0 = N cos φ - m g ( y-direction )
- m a = - N sin φ ( r-direction )
gives
tan φ = v2 / ( g R )

21. Variable
Angular Speed

22. Non-Uniform Circular Motion
Speed varies:
Velocity changes in direction + magnitude ⤇ points tangentially to the
circle
Both radial & tangential components of acceleration are nonzero
Tangential component of a = rate of change of speed
Tangential component of a is in the same (opposite) direction as the
velocity if the particle is speeding up (slowing down)
Exercise / Tutorial: Prove that

23. Examples
Roller coaster cars ⤇ slow down and speed up as they move around a
vertical loop
David swinging sling in a vertical circle

24. Problem 3
Analyze the forces as the roller coaster goes through the top of a hill,
the bottom of a valley, top of a loop, down the side of a loop

25. Problem 3: Solution
(1) Top of the hill
Centripetal force is supplied by gravity
& possibly even the safety harness
Normal reaction = N ≥ 0
Weight = m g
Fnet = N – m g (in vertically upward direction)
⇒ - centripetal force = N – m g
⇒ - m v1
2 / R1 = N – m g
How fast can the coaster can go until the rider just (barely) loses contact with
the seat ?
N = 0
⇒ m v1
2 / R1 = m g
⇒ v1
2 = g R1
At higher speeds, N = m ( g - v1
2 / R1 ) says that the normal force will be negative!
This just means that for v1
2 / R1 > g the rider will fly off the coaster ( N=0 ) unless
a safety harness supplies an extra downward force ( Fsafety ) pulling the rider
downward, providing the remaining centripetal force : m v1
2 / R1 = m g + Fsafety
velocity v1
N
mg
R1

26. Problem 3: Solution ...
(2) Bottom of the valley
Normal reaction = N
Weight = m g
Fnet = N – m g (in vertically upward direction)
⇒ centripetal force = N – m g
⇒ m v2
2 / R2 = N – m g
velocity v2
N
R2
mg

27. Problem 3: Solution ...
(3) Top of the loop
Normal reaction = N ≥ 0
Weight = m g
Fnet = - N – m g (in vertically upward direction)
⇒ - centripetal force = - N – m g
⇒ m v3
2 / R2 = N + m g
If the speed is too low, N = m ( v3
2 / R2 – g ) says that the normal force will be
negative ! This just means that for v3
2 / R2 < g, the car would fall off the track.
To prevent this, roller coasters have wheels on both sides of the track.
velocity v3
N
R2
mg

28. Problem 3: Solution ...
(4) Down the side of the loop
Normal reaction = N ≥ 0
Weight = m g
Fnet,x = N ( in radially inward direction )
⇒ centripetal force = N
⇒ m v4
2 / R2 = N
Fnet,y = - m g ( in vertically upward direction )
⇒ tangential force = - m g
⇒ - m aθ = - m g
⇒ aθ = g
N
R2
velocity v4
mg
aθ
aR
aθ
aR
a

29. Points to Remember
An object moving in a circle:
Always has a tangentially directed velocity
Always has a radially inward component of acceleration
Always has a net force acting on it
Has a tangential component of acceleration if its speed changes with
time

30. Problem 4
An object of mass m is constrained to move in a circle of radius r. Its
tangential acceleration is given by at = b + c t2
, where b and c are
constants. If v = v0
at t = 0, determine the radial component of the
acceleration
Radial acceleration is: