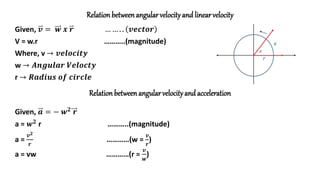
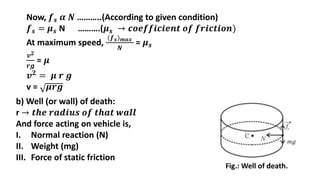
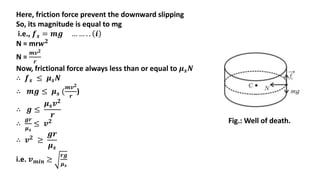
This document provides information about rotational dynamics and circular motion. It defines key terms like angular displacement, angular velocity, angular acceleration, and their relationships to linear displacement, velocity, and acceleration. It describes uniform and non-uniform circular motion. Centripetal force is introduced as the force providing the necessary acceleration for circular motion. Applications of uniform circular motion are discussed, including vehicles on horizontal and banked circular tracks and the well of death. The concept of a conical pendulum is also briefly mentioned.





![n → Frequency of an object to rotate
T → Periodic time / Period of circular motion
So, w = 2 𝝅 n
[ i.e. w = 2 𝝅 ×
𝟏
𝑻
] ……….( n =
𝟏
𝑻
)
Where, w → Angular Velocity](https://image.slidesharecdn.com/rotationaldynamicsintroduction-210516150622/85/PHYSICS-Rotational-dynamics-MAHARASHTRA-STATE-BOARD-10-320.jpg)




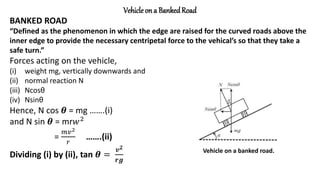
![APPLICATIONOF UCM
a) Vehicle along a horizontal circular track:
Theoretical proof:
In this, force acting on car is
(i) Weight (mg)
(ii) Normal reaction (N)
(iii) Force of friction (𝒇𝒔)
Here, mg = N …..(1)
And 𝒇𝒔 → 𝒄𝒆𝒏𝒕𝒓𝒊𝒑𝒆𝒕𝒂𝒍 𝒇𝒐𝒓𝒄𝒆 = 𝒎𝒓𝒘𝟐
= mr (
𝒗𝟐
𝒓𝟐) …….(v=wr)
= m
𝒗𝟐
𝒓
…….[from equation (1)]
∴ 𝒇𝒔 =
𝑵
𝒈
𝒗𝟐
𝒓
…….. (m =
𝑵
𝒈
)
∴ 𝒇𝒔 = 𝑵
𝒗𝟐
𝒓𝒈
→
𝒇𝒔
𝑵
=
𝒗𝟐
𝒓𝒈
Fig.: Vehicle on a horizontal road.](https://image.slidesharecdn.com/rotationaldynamicsintroduction-210516150622/85/PHYSICS-Rotational-dynamics-MAHARASHTRA-STATE-BOARD-16-320.jpg)
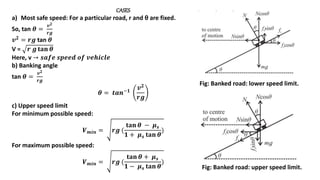



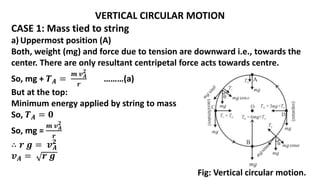
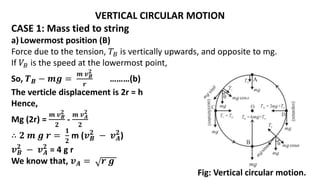

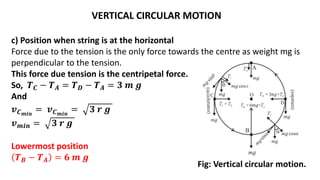
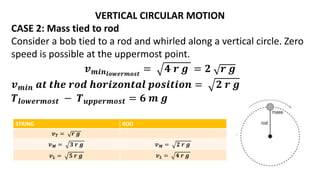



![Expression for KINETICENERGY
Consider
∴ 𝒎𝟏, 𝒎𝟐, 𝒎𝟑, … … .be individual masses of rigid body
∴ 𝒓𝟏, 𝒓𝟐, 𝒓𝟑, … … .be the distance between axis of rotation and point masses
Here, for individual mass of particle the K.E. will be
K.E. =
𝟏
𝟐
𝒎 𝒗𝟐
So, for all the point masses of the rotating body
Rotational K.E. =
𝟏
𝟐
𝒎𝟏 𝒗𝟏
𝟐
+
𝟏
𝟐
𝒎𝟐 𝒗𝟐
𝟐
+ …….+
𝟏
𝟐
𝒎𝑵 𝒗𝑵
𝟐
Rotational K.E. =
𝟏
𝟐
[ 𝒎𝟏 𝒗𝟏
𝟐
+ 𝒎𝟐 𝒗𝟐
𝟐
+ …….+ 𝒎𝑵 𝒗𝑵
𝟐
]
We know, v = r w
Rotational K.E. =
𝟏
𝟐
𝒎𝟏 𝒓𝟏
𝟐
𝒘𝟐 +
𝟏
𝟐
𝒎𝟐 𝒓𝟐
𝟐
𝒘𝟐 + …….+
𝟏
𝟐
𝒎𝑵 𝒓𝑵
𝟐
𝒘𝟐
Rotational K.E. =
𝟏
𝟐
[𝒎𝟏 𝒓𝟏
𝟐
+ 𝒎𝟐 𝒓𝟐
𝟐
+ …….+ 𝒎𝑵 𝒓𝑵
𝟐
] 𝒘𝟐
Rotational K.E. =
𝟏
𝟐
[ 𝒊=𝟏
𝑵
𝒎𝑵 𝒓𝑵
𝟐
] 𝒘𝟐
=
𝟏
𝟐
𝑰 𝒘𝟐 …………..[I = 𝒊=𝟏
𝑵
𝒎𝑵 𝒓𝑵
𝟐
]](https://image.slidesharecdn.com/rotationaldynamicsintroduction-210516150622/85/PHYSICS-Rotational-dynamics-MAHARASHTRA-STATE-BOARD-32-320.jpg)
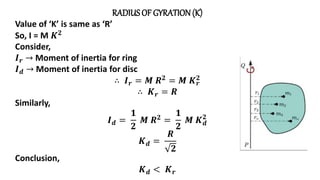
![Expression OF ‘I’ FOR UNIFORMRING
Moment of Inertia of a ring.
Said to be uniform if mass of any body
practically situated uniformly on the
circumference of circle
It entire mass practically at equal
distance from centre that is mass (m)
Also distance R is same for the ring
So, expression is,
I = M 𝑹𝟐
….[For ring]](https://image.slidesharecdn.com/rotationaldynamicsintroduction-210516150622/85/PHYSICS-Rotational-dynamics-MAHARASHTRA-STATE-BOARD-33-320.jpg)

![Expression OF ‘I’ FOR UNIFORMDISC
So, surface density ( 𝜎 ) =
𝑑𝑚
2 𝜋 𝑟 𝑑𝑟
∴ 𝑑𝑚 = 2 𝜋 𝑟 𝑑𝑟 𝜎
Here, r → 𝑖𝑠 𝑠𝑎𝑚𝑒 𝑡ℎ𝑟𝑜𝑢𝑔ℎ𝑜𝑢𝑡 𝑏𝑜𝑑𝑦
𝐼𝑟 = 𝑑𝑚 𝑟2
For whole,
By integration the inertia:
I = 0
𝑅
𝐼𝑟 = 0
𝑅
𝑑𝑚 𝑟2
= 0
𝑅
2 𝜋 𝑟 𝜎 𝑟2
𝑑𝑟
= 0
𝑅
2 𝜋 𝜎 𝑟3 dr
= 2 π 𝜎 0
𝑅
𝑟3 dr
= 2 π 𝜎 [
𝑟4
4
]0
𝑅
= 2 π 𝜎
𝑅4
4
=
1
2
𝜋 𝜎 𝑅4
Moment of Inertia of a disk.
I =
𝟏
𝟐
𝝅
𝑴
𝝅𝑹𝟐 𝑹𝟒
=
𝟏
𝟐
𝑴 𝑹𝟐 …(For disc)](https://image.slidesharecdn.com/rotationaldynamicsintroduction-210516150622/85/PHYSICS-Rotational-dynamics-MAHARASHTRA-STATE-BOARD-35-320.jpg)