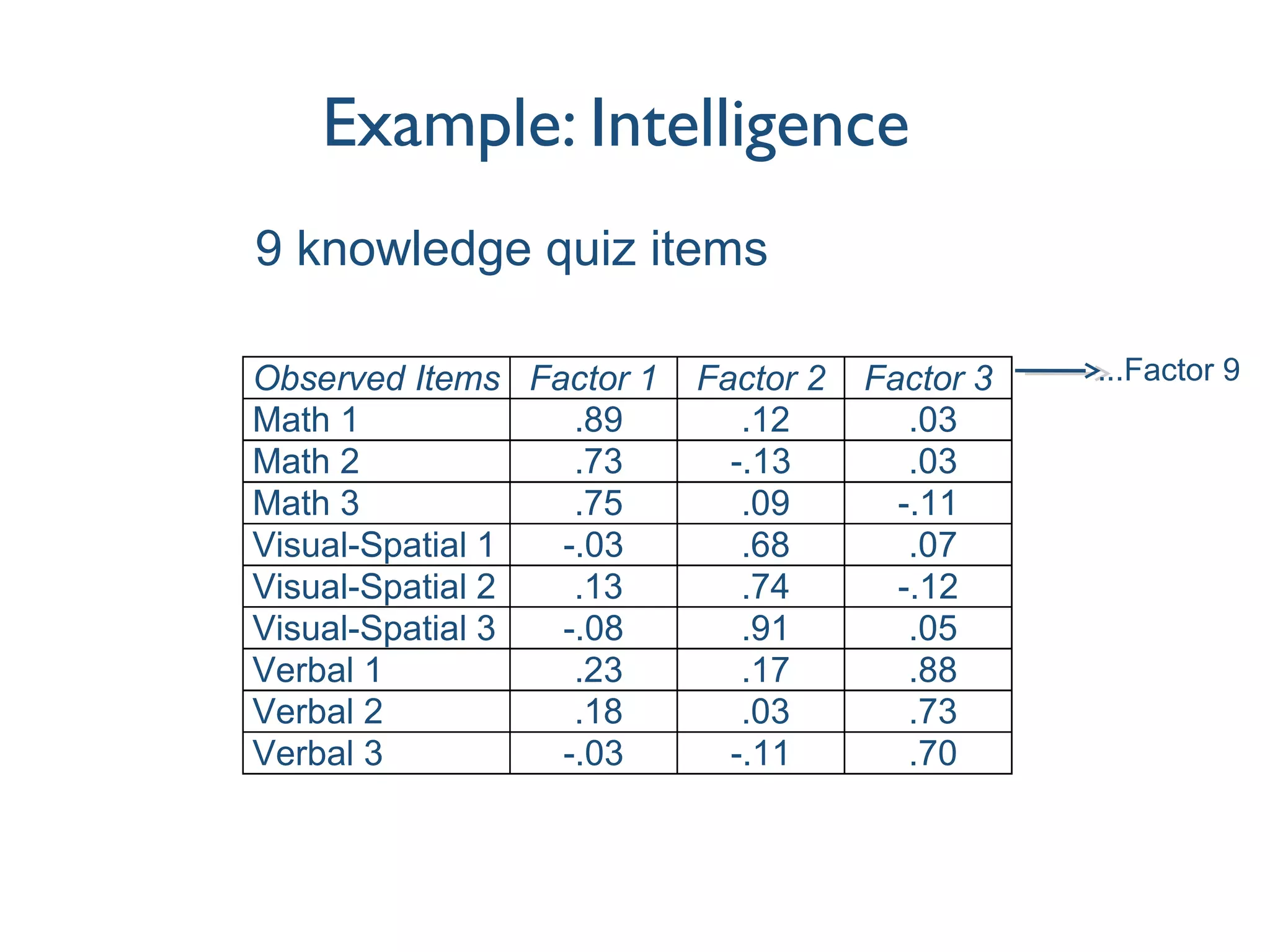
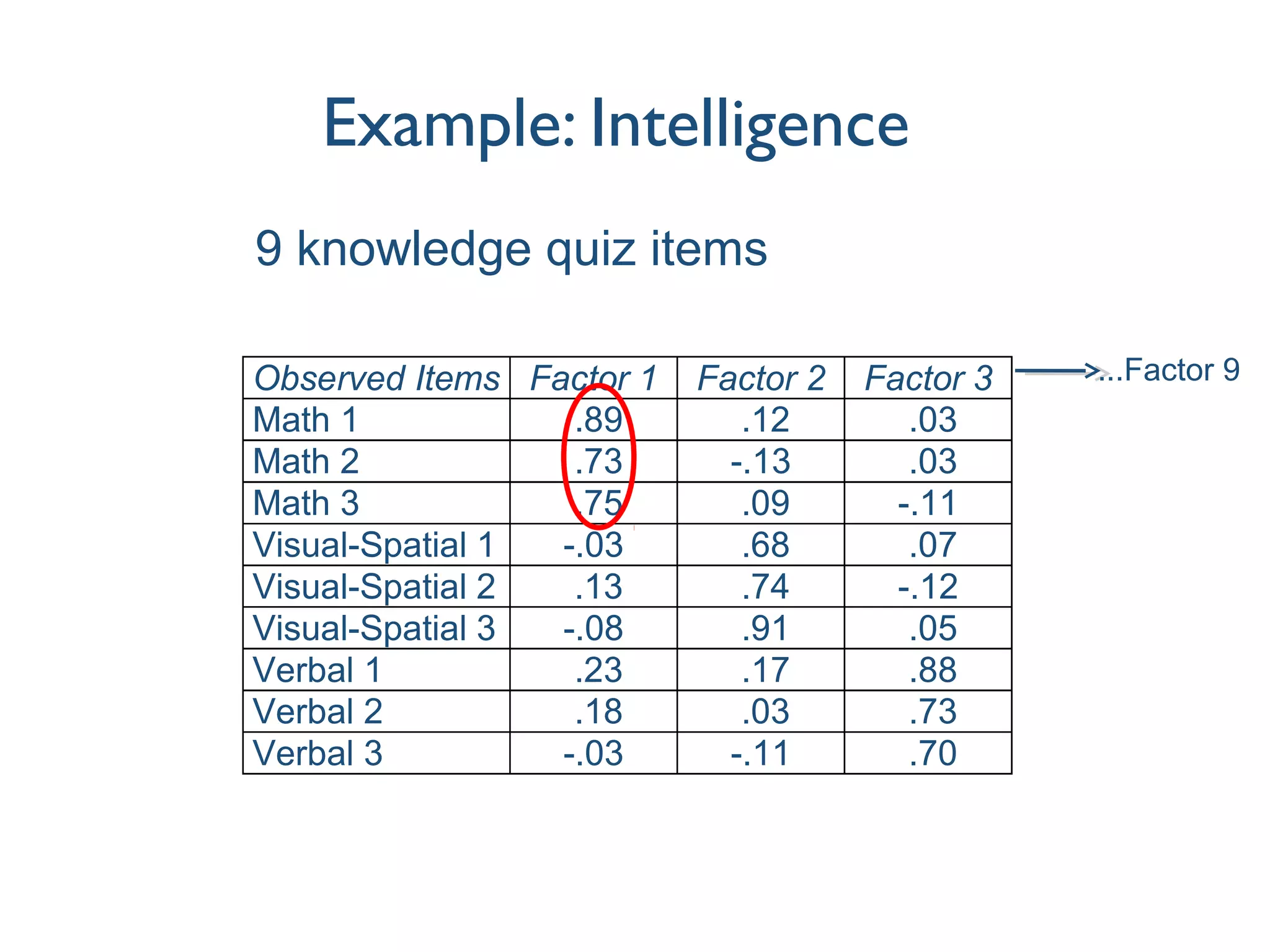
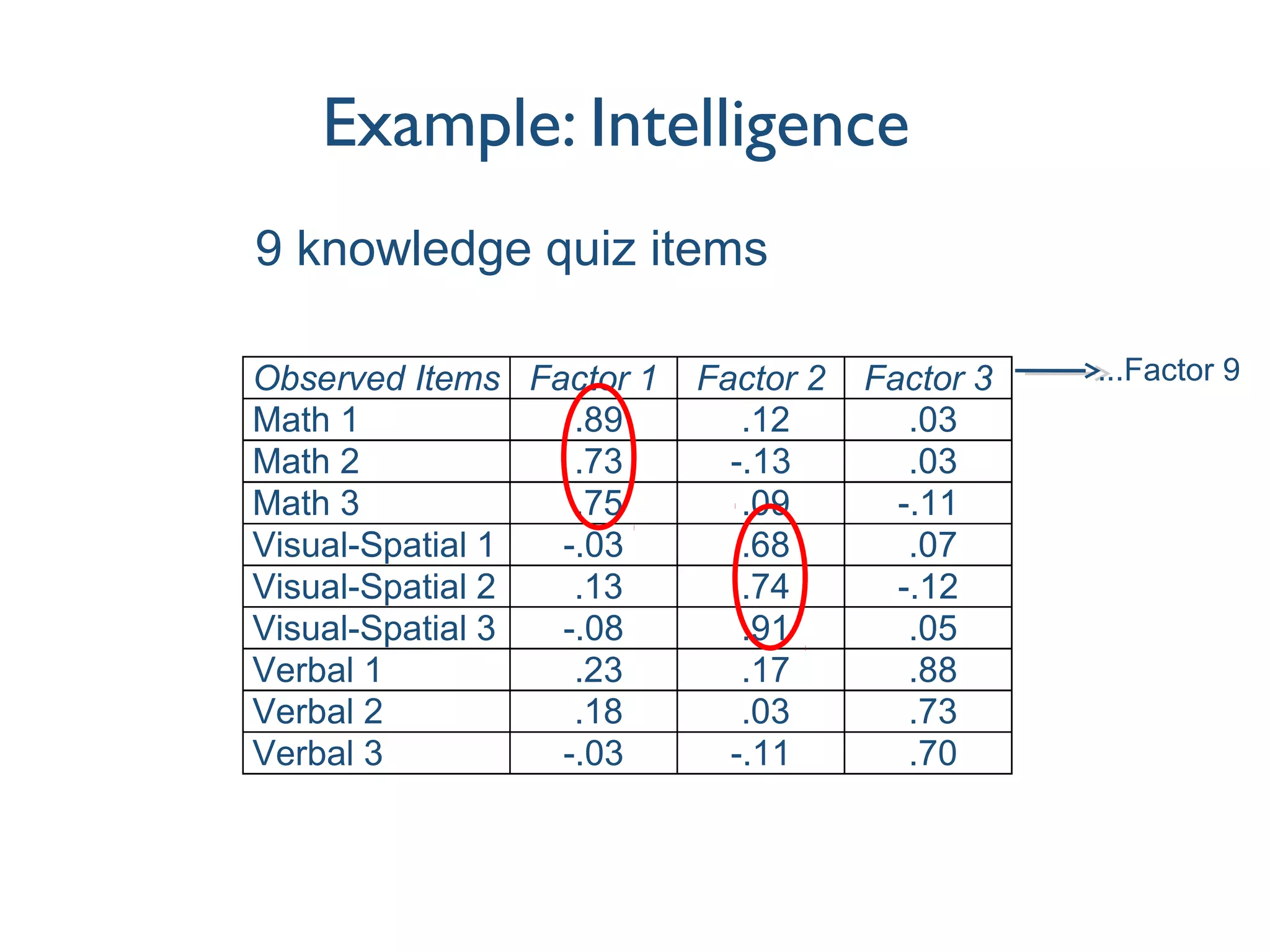
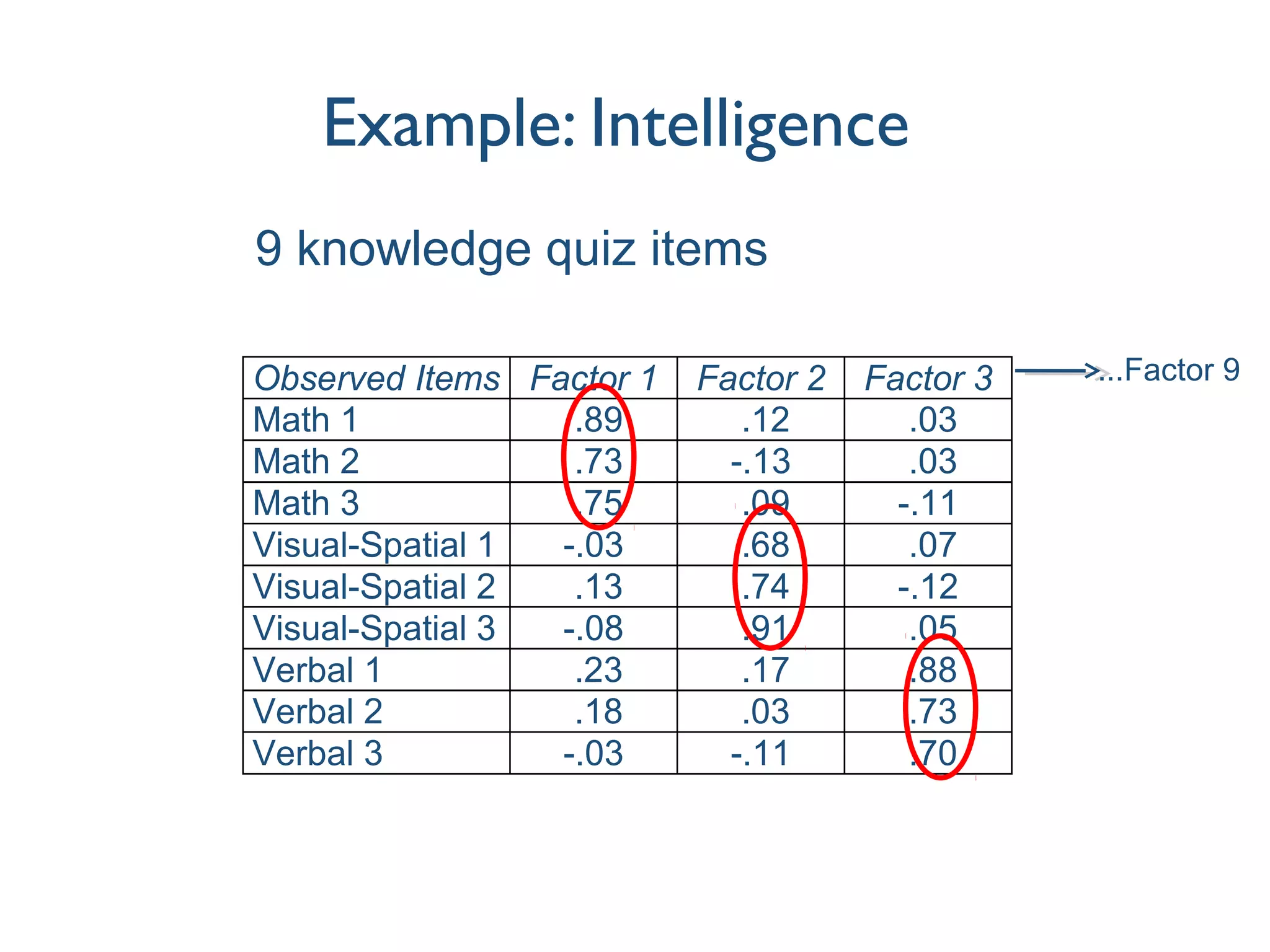
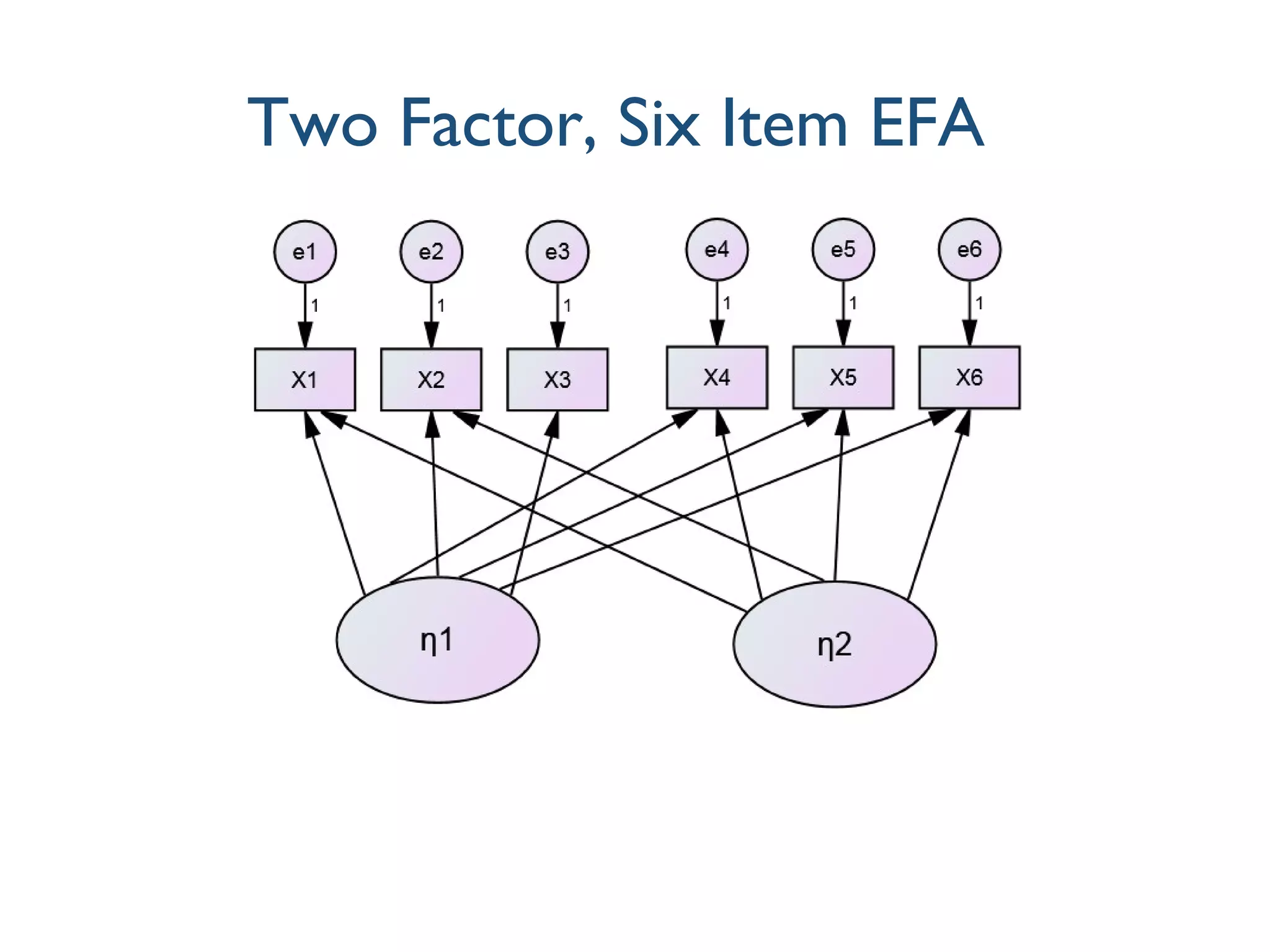
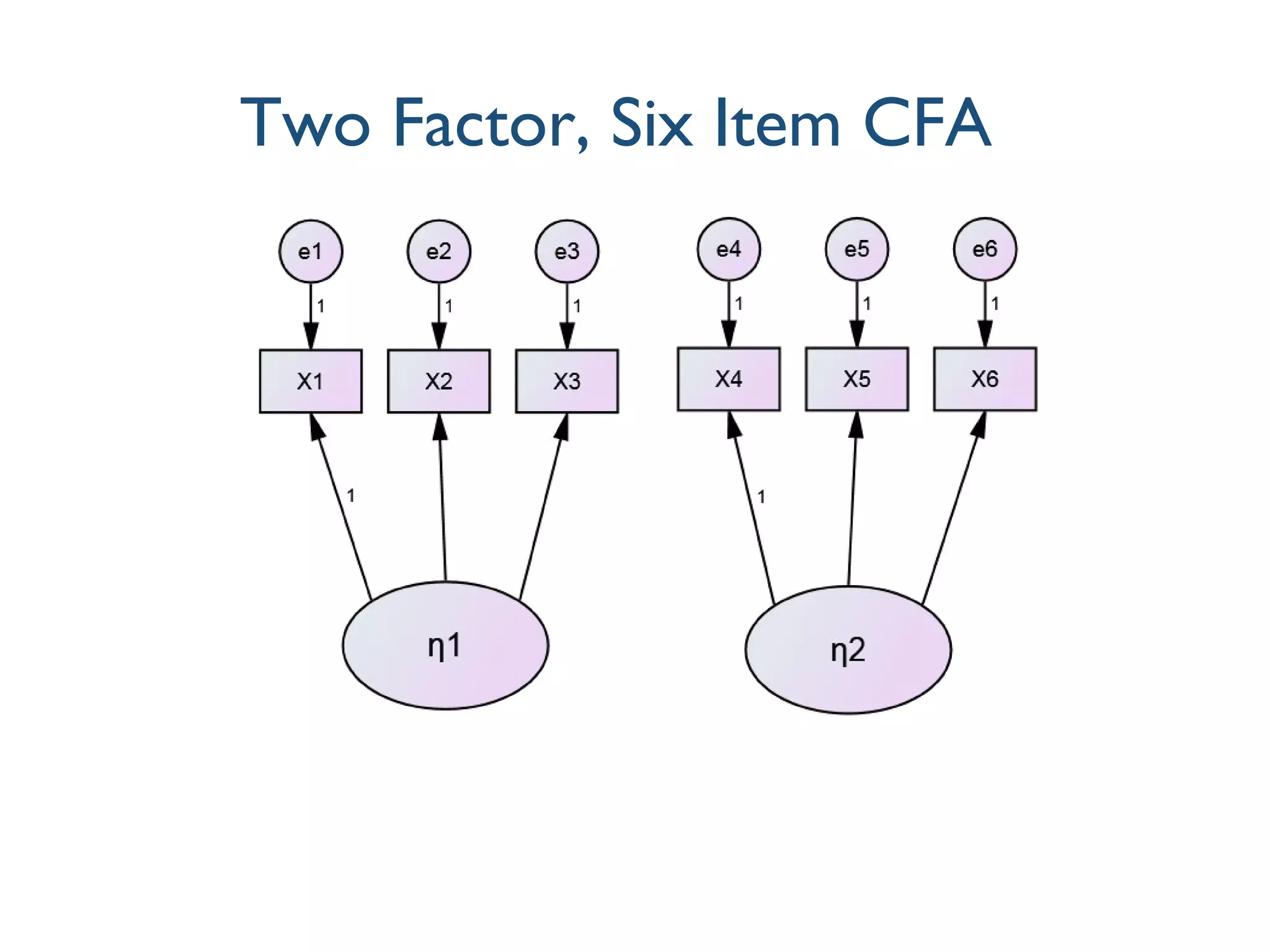
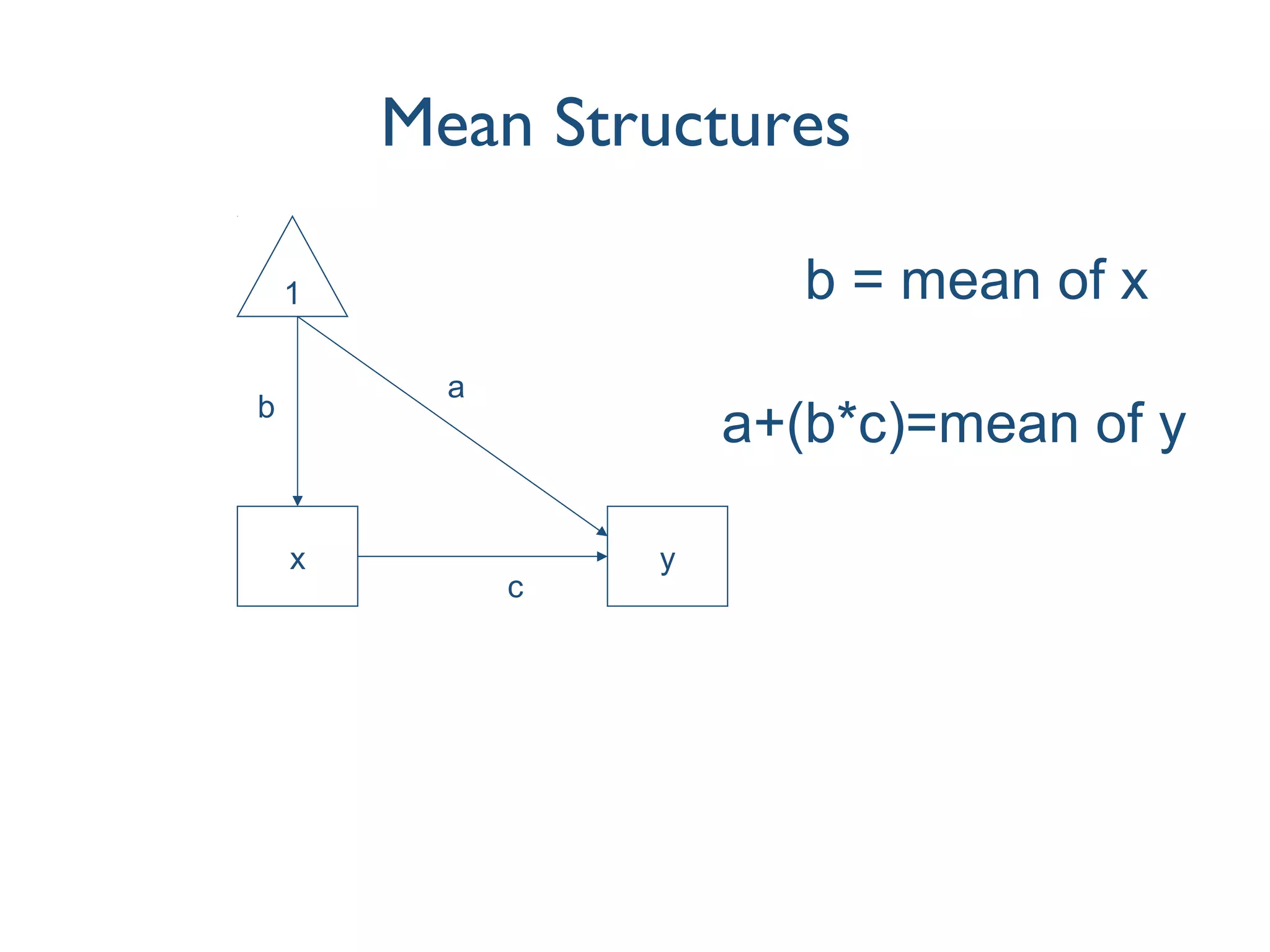
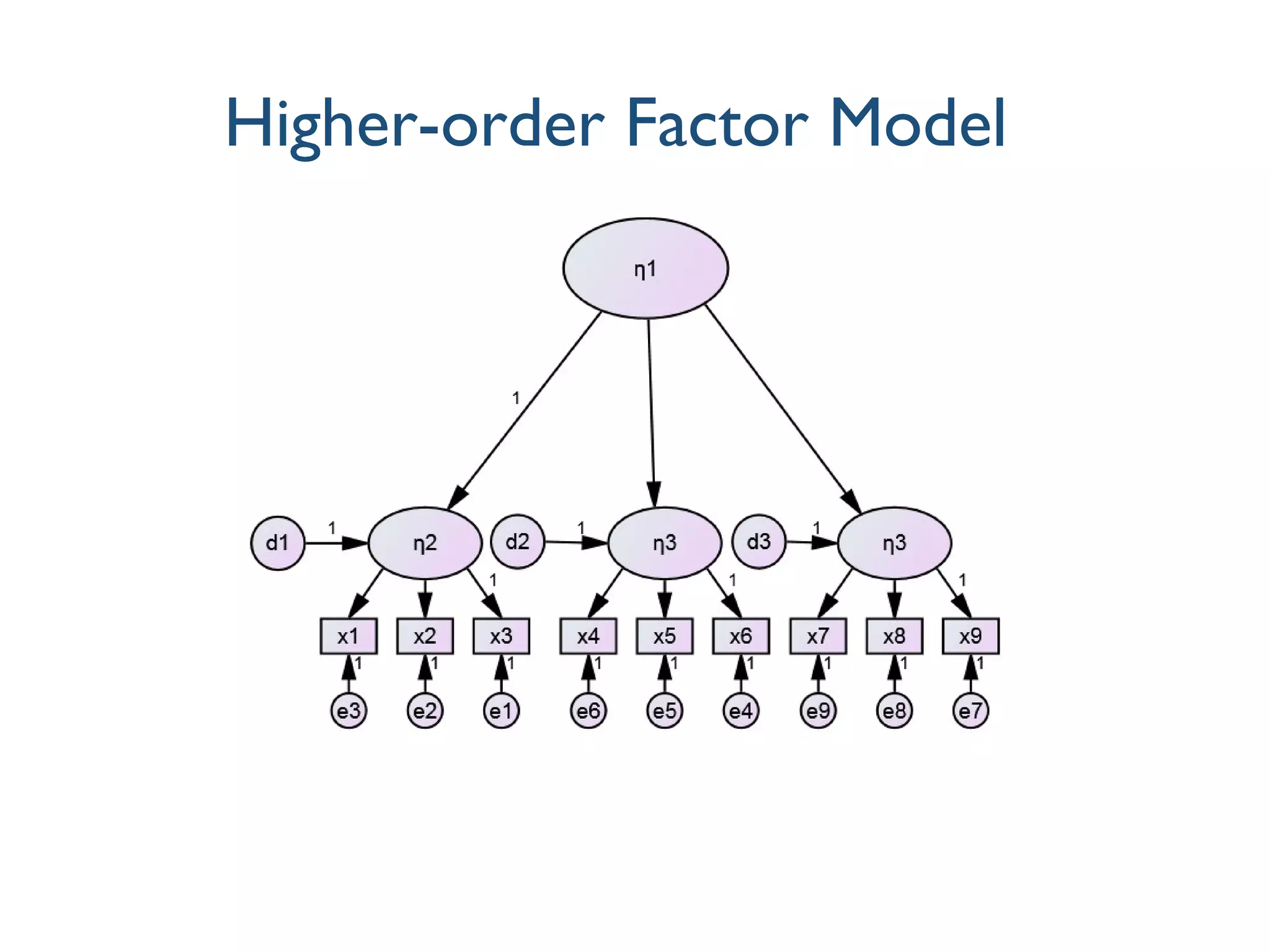
This document discusses various techniques for measuring latent variables using factor analysis, including exploratory factor analysis (EFA), confirmatory factor analysis (CFA), fixing the scale of latent variables, modeling mean structures, the use of formative indicators, item parcelling, and higher-order factor models. EFA is described as an initial, inductive approach to uncover the underlying factor structure in observed variables, while CFA provides a confirmatory, theory-driven approach to explicitly test a hypothesized measurement model. Additional topics covered include identifying latent variables, modeling means of observed and latent variables, and distinguishing between reflective and formative indicator specifications.