Downloaded 686 times
Uploaded byUniversity of Southampton
Introduction to Structural Equation Modeling
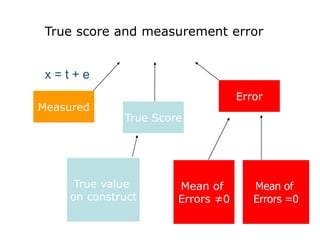
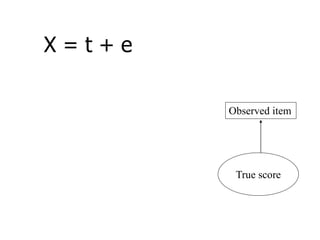
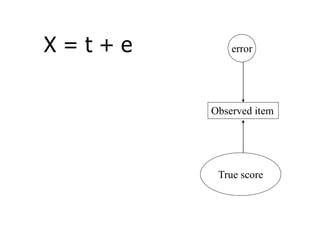
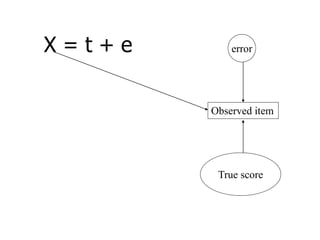
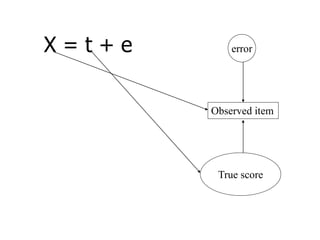
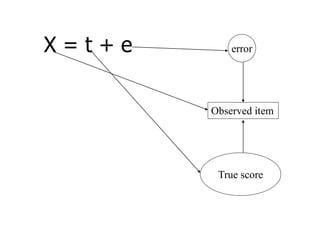
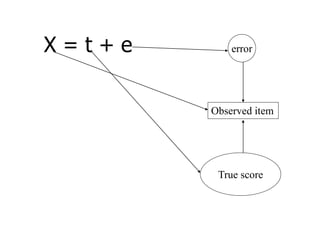
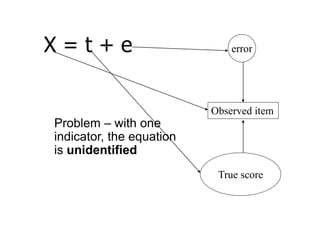
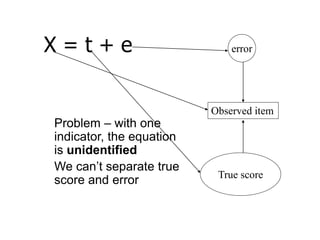
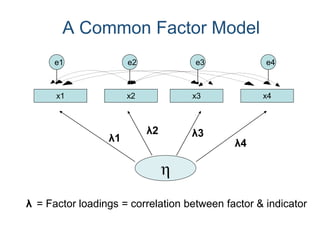
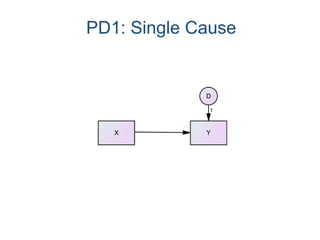
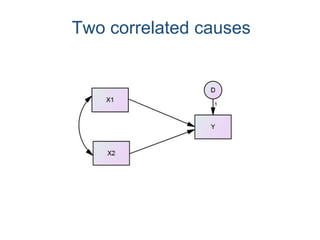
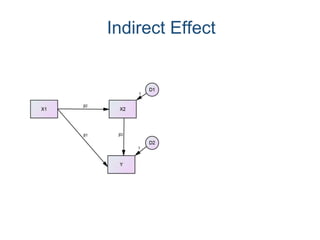
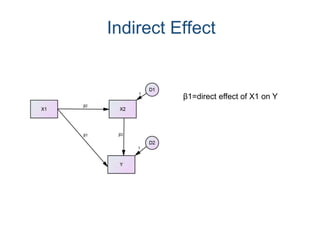
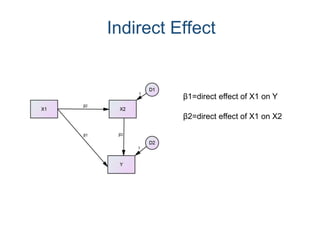
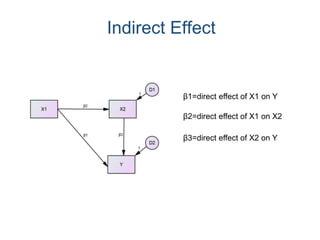
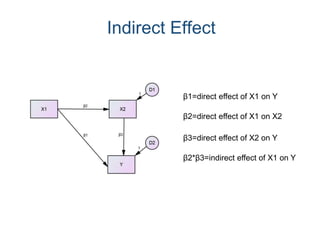
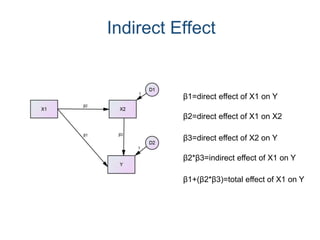
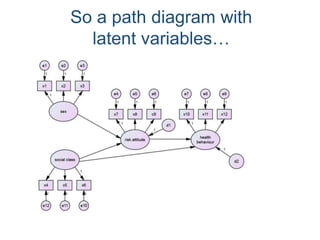
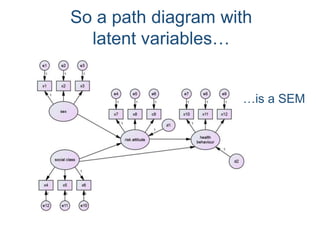
SEM is not a single statistical technique but rather integrates multiple multivariate techniques like factor analysis, path analysis, and regression into a unified framework. It allows modeling of complex latent constructs that are measured with error through multiple observed variables. Path analysis using latent variables can partition variance between true scores on latent variables and measurement error, and examine direct, indirect, and total effects in a system of relationships between variables.
More Related Content
Similar to Introduction to Structural Equation Modeling
More from University of Southampton
Introduction to Structural Equation Modeling
- 2.
- 3. What is SEM? •SEM is not one statistical ‘technique’
- 4. What is SEM? •SEM is not one statistical ‘technique’ • It integrates a number of different multivariate techniques into one model fitting framework
- 5. What is SEM? •SEM is not one statistical ‘technique’ • It integrates a number of different multivariate techniques into one model fitting framework • It is an integration of: – Measurement theory – Factor (latent variable) analysis – Path analysis – Regression – Simultaneous equations
- 6.
- 7. Useful for Research Questionsthat.. • Involve complex, multi-faceted constructs that are measured with error
- 8. Useful for Research Questionsthat.. • Involve complex, multi-faceted constructs that are measured with error • That specify ‘systems’ of relationships rather than a dependent variable and a set of predictors
- 9. Useful for Research Questionsthat.. • Involve complex, multi-faceted constructs that are measured with error • That specify ‘systems’ of relationships rather than a dependent variable and a set of predictors • Focus on indirect (mediated) as well as direct effects of variables on other variables
- 10.
- 11. Also Known as •Covariance Structure Analysis
- 12. Also Known as •Covariance Structure Analysis • Analysis of Moment Structures
- 13. Also Known as •Covariance Structure Analysis • Analysis of Moment Structures • Analysis of Linear Structural Relationships (LISREL)
- 14. Also Known as •Covariance Structure Analysis • Analysis of Moment Structures • Analysis of Linear Structural Relationships (LISREL) • Causal Modeling
- 15. Software for SEM •There are a lot of software packages that can fit SEMs
- 16. Software for SEM •There are a lot of software packages that can fit SEMs • The original and best known is Lisrel, developed by Joreskog and Sorbom
- 17. Software for SEM •There are a lot of software packages that can fit SEMs • The original and best known is Lisrel, developed by Joreskog and Sorbom • Mplus, EQS, Amos, Calis, Mx, SEPATH, Tetrad, R, stata
- 18. Software for SEM •There are a lot of software packages that can fit SEMs • The original and best known is Lisrel, developed by Joreskog and Sorbom • Mplus, EQS, Amos, Calis, Mx, SEPATH, Tetrad, R, stata • Some have downloadable student versions
- 19. SEM can bethought of as Path Analysis using Latent Variables
- 20. What are LatentVariables?
- 21. What are LatentVariables? • Most social scientific concepts are not directly observable, e.g. intelligence, social capital
- 22. What are LatentVariables? • Most social scientific concepts are not directly observable, e.g. intelligence, social capital • This makes them hypothetical or ‘latent’ constructs
- 23. What are LatentVariables? • Most social scientific concepts are not directly observable, e.g. intelligence, social capital • This makes them hypothetical or ‘latent’ constructs • We can measure latent variables using observable indicators
- 24. What are LatentVariables? • Most social scientific concepts are not directly observable, e.g. intelligence, social capital • This makes them hypothetical or ‘latent’ constructs • We can measure latent variables using observable indicators • We can think of the variance of a questionnaire item as being caused by: – The latent construct we want to measure – Other factors (error/unique variance)
- 25. x = t+ e Measured True Score Error Random Error Systematic Error True score and measurement error Mean of Errors =0 Mean of Errors ≠0 True value on construct
- 27. X = t+ e
- 28. X = t+ e Observed item
- 29. X = t+ e Observed item True score
- 30. X = t+ e Observed item True score error
- 31. X = t+ e Observed item True score error
- 32. X = t+ e Observed item True score error
- 33. X = t+ e Observed item True score error
- 34. X = t+ e Observed item True score error
- 35. X = t+ e Observed item True score error Problem – with one indicator, the equation is unidentified
- 36. X = t+ e Observed item True score error Problem – with one indicator, the equation is unidentified We can’t separate true score and error
- 37. Multiple Indicator LatentVariables
- 38. Multiple Indicator LatentVariables • To identify t & e components we need multiple indicators of the latent variable
- 39. Multiple Indicator LatentVariables • To identify t & e components we need multiple indicators of the latent variable • With multiple indicators we can use a latent variable model to partition variance
- 40. Multiple Indicator LatentVariables • To identify t & e components we need multiple indicators of the latent variable • With multiple indicators we can use a latent variable model to partition variance • e.g. principal components analysis transforms correlated variables into uncorrelated components
- 41. Multiple Indicator LatentVariables • To identify t & e components we need multiple indicators of the latent variable • With multiple indicators we can use a latent variable model to partition variance • e.g. principal components analysis transforms correlated variables into uncorrelated components • We can then use a reduced set of components to summarise the observed associations
- 42. A Common FactorModel η λ1 λ2 λ3 λ4 e1 e2 e3 e4 x1 x2 x3 x4 = Factor loadings = correlation between factor & indicatorλ
- 43. Benefits of LatentVariables
- 44. Benefits of LatentVariables • Most social concepts are complex and multi- faceted
- 45. Benefits of LatentVariables • Most social concepts are complex and multi- faceted • Using single measures will not adequately cover the full conceptual map
- 46. Benefits of LatentVariables • Most social concepts are complex and multi- faceted • Using single measures will not adequately cover the full conceptual map • Removes/reduces random error in measured construct
- 47. Benefits of LatentVariables • Most social concepts are complex and multi- faceted • Using single measures will not adequately cover the full conceptual map • Removes/reduces random error in measured construct • Random error in dependent variables -> estimates unbiased but less precise
- 48. Benefits of LatentVariables • Most social concepts are complex and multi- faceted • Using single measures will not adequately cover the full conceptual map • Removes/reduces random error in measured construct • Random error in dependent variables -> estimates unbiased but less precise • Random error in independent variables -> attenuates regression coefficients toward zero
- 49. Remember SEM can bethought of as Path Analysis using Latent Variables
- 50. Remember SEM can bethought of as Path Analysis using Latent Variables We now know about latent variables, what about path analysis?
- 51.
- 52. Path Analysis • Thediagrammatic representation of a theoretical model using standardised notation
- 53. Path Analysis • Thediagrammatic representation of a theoretical model using standardised notation • Regression equations specified between measured variables
- 54. Path Analysis • Thediagrammatic representation of a theoretical model using standardised notation • Regression equations specified between measured variables • ‘Effects’ of predictor variables on criterion/dependent variables can be: – Direct – Indirect – Total
- 55.
- 56. Path Diagram notation Measuredlatent variable Observed / manifest variable
- 57. Path Diagram notation Errorvariance / disturbance term Measured latent variable Observed / manifest variable
- 58. Path Diagram notation Errorvariance / disturbance term Measured latent variable Observed / manifest variable Covariance / non-directional path
- 59. Path Diagram notation Errorvariance / disturbance term Measured latent variable Observed / manifest variable Covariance / non-directional path Regression / directional path
- 60.
- 61.
- 62.
- 63.
- 64. Indirect Effect β1=direct effectof X1 on Y
- 65. Indirect Effect β1=direct effectof X1 on Y β2=direct effect of X1 on X2
- 66. Indirect Effect β1=direct effectof X1 on Y β2=direct effect of X1 on X2 β3=direct effect of X2 on Y
- 67. Indirect Effect β1=direct effectof X1 on Y β2=direct effect of X1 on X2 β3=direct effect of X2 on Y β2*β3=indirect effect of X1 on Y
- 68. Indirect Effect β1=direct effectof X1 on Y β2=direct effect of X1 on X2 β3=direct effect of X2 on Y β2*β3=indirect effect of X1 on Y β1+(β2*β3)=total effect of X1 on Y
- 69. So a pathdiagram with latent variables…
- 70. So a pathdiagram with latent variables…
- 71. So a pathdiagram with latent variables… …is a SEM