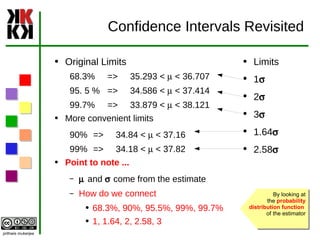
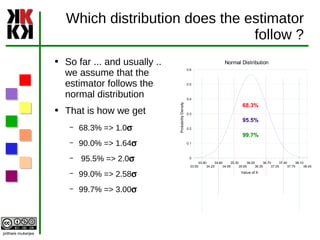
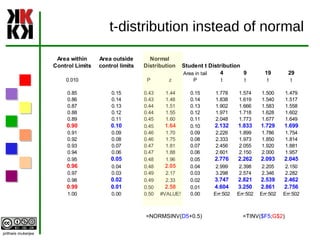
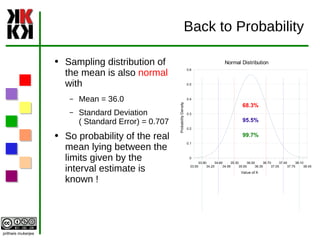
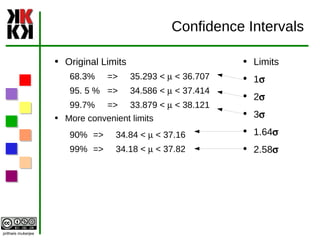
The document discusses estimation and different types of estimates used to estimate population parameters based on sample data. Point estimates provide a single value while interval estimates provide a range of values. Good estimators are unbiased, efficient, and consistent. Common point estimators are the sample mean and sample standard deviation. Interval estimates use the point estimate plus/minus a margin of error calculated from the standard error. Confidence intervals provide a probability that the population parameter lies within the interval estimate.

1. Estimation S Q U A N T T E C H I N T E U Q I A S E V I T 1 0 S

2. Why Estimation ? [ From ] Inference For a given population Various statistical parameters are GIVEN or KNOWN Mean, Standard Deviation etc Task was to interpret them and take managerial decisions How many shirts to be stocked in the store ? Is the machine setup faulty ? Should we fix it [ To ] Estimation For the given population or sample Various statistical parameters are NOT KNOWN So managerial decisions cannot be taken UNLESS we can estimate the parameters

3. Two kinds of Estimates Point Estimate A single number that is used to estimate a given population parameter Mean Age = 22.3 Interval Estimate A range of values used to estimate a population parameter Mean Age is between 21.5 and 23 Difficulty of point estimate It is either right or wrong ! No way to know the quantum of error in the estimate Needs to accompanied by another estimate of the error that could have happened !!

4. Estimator Estimator A sample statistic that is used to estimate a population parameter Estimate A specific value of the statistic that is observed

5. Criteria for a Good Estimator Unbiased Example : Mean of the sampling distribution of sample means taken from the population is equal to the population mean itself. Efficient Depends on the standard error of the statistic Standard error = standard deviation of the sampling distribution If standard error is low, estimator is efficient Consistent When sample size increases the value of the statistic comes closer and closer to the value of the parameter Sufficient Uses all information that can be extracted from sample

6. Point Estimate Estimate of Mean Sample Mean S x x = n Estimate of Standard Deviation S (x – x) 2 s 2 = n – 1 We cannot use the lower statistic because S (x – x) 2 s 2 = n because it can be shown that it has a bias !

7. Where are the errors here ? Potential number of patrons at a very popular musical concert that is always sold out .. Estimator : Average number of tickets sold Telephone calls are billed by whole minutes even if the duration is a fraction. What is the average length of a call ? Estimator : Average billing for all calls made over a day / Rate per minute

8. Interval Estimate An interval estimate describes a range of values within which a population parameter is likely to lie Consider an interval estimate for the mean Start with a point estimate Find the likely error of this estimate Standard error is standard deviation of the estimator Make an interval estimate Defined in terms of the estimate and the standard error Find the probability that mean will fall in this interval estimate

9. Example Estimate the average battery life of a car in months From a sample size of 200 we get x = 36 Standard error of sample mean s s x = = 0.707 assuming s = 10 Now we can make an interval estimates like x – s x < m < x + s x => 35.293 < m < 36.707 x – 2 s x < m < x + 2 s x => 34.586 < m < 37.414 x – 3 s x < m < x + 3 s x => 33.879 < m < 38.121

10. Back to Probability Sampling distribution of the mean is also normal with Mean = 36.0 Standard Deviation ( Standard Error) = 0.707 So probability of the real mean lying between the limits given by the interval estimate is known ! 68.3% 95.5% 99.7%

11. Interval Estimate of Mean Probabilities are as follows 68.3% => 35.293 < m < 36.707 95. 5 % => 34.586 < m < 37.414 99.7% => 33.879 < m < 38.121 Here we note that the probabilities are odd, fractional kind of numbers ... So how can we have simpler probabilities like 50% or 90% probability ?

12. Confidence Interval We observe that in a normal distribution 90% of the values lie within 1.64 s of mean 99% of the values lie within 2.58 s of mean So we redefine our interval estimates as 90% => 34.84 < m < 37.16 99% => 34.18 < m < 37.82

13. Confidence Intervals Original Limits 68.3% => 35.293 < m < 36.707 95. 5 % => 34.586 < m < 37.414 99.7% => 33.879 < m < 38.121 More convenient limits 90% => 34.84 < m < 37.16 99% => 34.18 < m < 37.82 Limits 1 s 2 s 3 s 1.64 s 2.58 s

14. Is a “higher” confidence interval always better ? I am 99.999% sure that the average age of this class lies between 1 year and 50 years Does this really help you in anyway ? I am 95% sure that the average age of this class lies between 23 and 26 years This gives me a far better idea of where the average age of the class lies This information is better than the first information

15. 95% confident that the mean battery life lies between 30 – 42 months Does NOT mean that There is 95% probability that the mean life of all our batteries falls within the interval established from this one sample It DOES mean that If we select many random samples of the same size and calculate a confidence interval for each of these samples then 95% of these intervals will contain the population mean

16. Calculation of Confidence Interval Example A large automotive parts wholesalers needs an estimate of the mean life that he can expect from a windshield wiper under normal driving conditions It is known that the standard deviation of the population life is 6 months Observations from 1 simple random sample of 100 blades is as follows Sample Size n = 100 Sample Mean x = 21 months Population standard deviation s = 6 months

17. 95% Confidence Interval Standard Error s s x = 6 = = 0.6 months 95% confidence level will include 47.5 % on each side of the mean Sample size is > 30 so we can assume that the sample mean follows a normal distribution In a normal distribution 95% values lie within 1.96 times the standard deviation 95 % values of the sample mean lie within 1.96 times the standard error

18. Upper Confidence Limit Lower Confidence Limit Upper Confidence Limit x + 1.96 s x = 21 + 1.96 ( 0.6) = 22.18 months Lower Confidence Limit x – 1.96 s x = 21 – 1.96 ( 0.6) = 19.82 months Two major assumptions Standard Deviation of Population is known In reality this is may not be known The sampling distribution follows the normal distribution This assumption is valid only if the sample size is more than 30.

19. Standard deviation is not known When Standard Deviation Known Standard Error of the Sample mean s s x = When Standard Deviation is not Known Standard Error of the sample mean s s x = S (x - x) 2 s = n - 1 ^ ^ ^

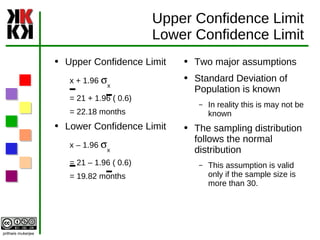
20. How do we get this interval [Usually] we are trying to estimate the population mean m We have an estimator E which [ in most cases ] is the sample mean. E follows a distribution that has mean m and standard error s We create a statistic Q = (E – m )/ s Q follows a some distribution ( normal ? T ? ) We identify two values Q 1 , Q 2 such that probability of Q falling between Q 1 and Q 2 is equal to required confidence P Interval is E – Q 1 s < m < E + Q 2 s

21. What is our goal ? What is known ? E, s , P What is to be calculated Q 1 , Q 2 What is the objective To be confident that Probability of m Lying between E – Q 1 s and E + Q 2 s Is equal to P

22. What are the steps Identify an estimator What distribution does the estimator follow ? Is the standard deviation known ? If not what is the estimator for the standard deviation Is the sample size big enough ? Get a value of the estimate Get a value of the standard error for the estimator Set an appropriate confidence level in terms of probability From the graph / table of the sampling distribution get the upper and lower limits in terms of estimate and the standard error

23. Confidence Intervals Revisited Original Limits 68.3% => 35.293 < m < 36.707 95. 5 % => 34.586 < m < 37.414 99.7% => 33.879 < m < 38.121 More convenient limits 90% => 34.84 < m < 37.16 99% => 34.18 < m < 37.82 Point to note ... m and s come from the estimate How do we connect 68.3%, 90%, 95.5%, 99%, 99.7% 1, 1.64, 2, 2.58, 3 Limits 1 s 2 s 3 s 1.64 s 2.58 s By looking at the probability distribution function of the estimator

24. Sample Size in Estimation What should be the sample size such that with a known population standard deviation, the sample size should be adequate to ensure an adequate confidence interval ?

25. Which distribution does the estimator follow ? So far ... and usually .. we assume that the estimator follows the normal distribution That is how we get 68.3% => 1.0 s 90.0% => 1.64 s 95.5% => 2.0 s 99.0% => 2.58 s 99.7% => 3.00 s 68.3% 95.5% 99.7%

26. The Student's t distribution Used when Standard deviation of the population is NOT known AND Sample size is less than 30 When this happens we cannot use the Normal distribution but must look up the tables for the T distribution

27. t-distribution instead of normal =NORMSINV( D5 +0.5) =TINV( $F5 ; G$2 )

28. Usage of t-table The probability that we are working with IS NOT the probability that the estimated value will fall inside the confidence interval INSTEAD It is the probability that the estimated value will fall OUTSIDE the confidence interval This probability is defined as a Confidence = 1 – a Degree of Freedom 1 – sample size

29. Binomial Distribution / Proportions We have a binomial distribution with p as the success probability 20% student population are engineers 45% of employees population are married We need to have an estimate of p Estimator is proportion p from sample Assumptions Estimator follows normal distribution m = np Standard error of estimate

30. Example Sample = 75 Fraction graduate p = 0.4 Fraction not graduate q = 0.6 Estimate of p = 0.4 Standard Error for Estimator = 0.057 99% confidence interval Z = 2.58 LCL 0.4 – 0.057 * 2.58 = 0.253 UCL 0.4 + 0.057 * 2.58 = 0.547