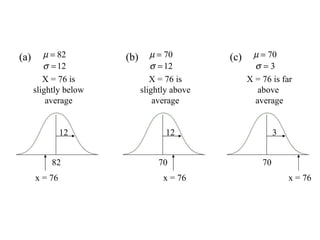
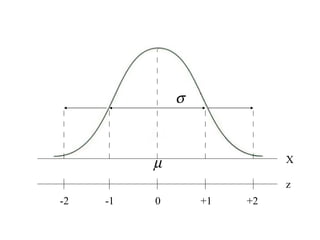
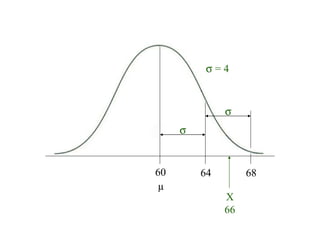
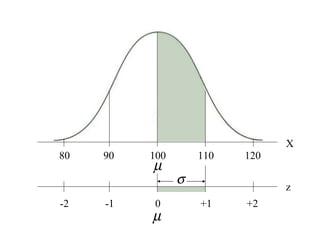
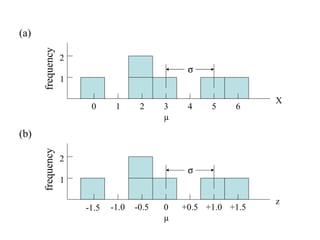
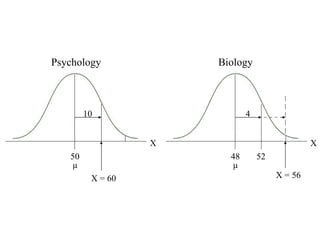
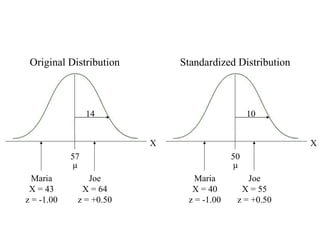
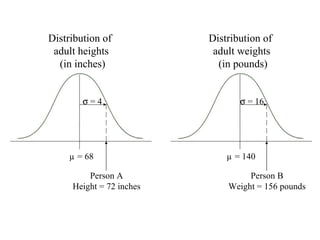
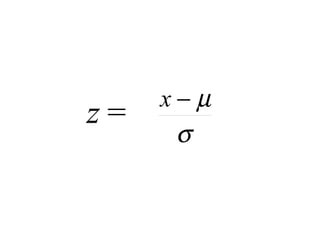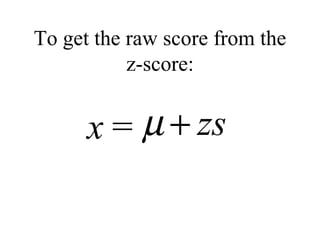This document discusses z-scores and how they are used to standardize distributions. A z-score specifies the position of a data point within a distribution by measuring its distance from the mean in units of standard deviations. The mean of a standardized distribution with z-scores is 0 and the standard deviation is 1. Converting raw scores to z-scores transforms distributions to have the same shape while accounting for different means and standard deviations. Z-scores allow for comparison of data points from different distributions.

1. Chapter 5: z-Scores

2. Normal curve distribution comparisons 12 82 x = 76 (a) X = 76 is slightly below average 12 70 x = 76 (b) X = 76 is slightly above average 3 70 x = 76 (c) X = 76 is far above average

3. Definition of z-score A z-score specifies the precise location of each x-value within a distribution. The sign of the z-score (+ or - ) signifies whether the score is above the mean (positive) or below the mean (negative). The numerical value of the z-score specifies the distance from the mean by counting the number of standard deviations between X and µ.

4. Normal curve segmented by sd’s X z -2 -1 0 +1 +2

5. Example 5.2 A distribution of exam scores has a mean (µ) of 50 and a standard deviation (σ) of 8.

6. Z formula

7. Normal curve with sd’s    = 4 60 64 68 µ X 66

8. Example 5.5 A distribution has a mean of µ = 40 and a standard deviation of  = 6.

9. To get the raw score from the z-score:

10. If we transform every score in a distribution by assigning a z-score, new distribution: Same shape as original distribution Mean for the new distribution will be zero The standard deviation will be equal to 1

11. Z-distribution X z -2 -1 0 +1 +2 100 110 120 90 80

12. A small population 0, 6, 5, 2, 3, 2 N=6 x x - µ (x - µ) 2 0 0 - 3 = -3 9 6 6 - 3 = +3 9 5 5 - 3 = +2 4 2 2 - 3 = -1 1 3 3 - 3 = 0 0 2 2 - 3 = -1 1

13. Frequency distributions with sd’s 2 1 0 1 2 3 4 5 6 µ  X frequency (a) 2 1 -1.5 -1.0 -0.5 0 +0.5 +1.0 +1.5 µ  z frequency (b)

14. Let’s transform every raw score into a z-score using: x = 0 x = 6 x = 5 x = 2 x = 3 x = 2 = -1.5 = +1.5 = +1.0 = -0.5 = 0 = -0.5

15. Z problem computation Mean of z-score distribution : Standard deviation: z z - µ z (z - µ z ) 2 -1.5 -1.5 - 0 = -1.5 2.25 +1.5 +1.5 - 0 = +1.5 2.25 +1.0 +1.0 - 0 = +1.0 1.00 -0.5 -0.5 - 0 = -0.5 0.25 0 0 - 0 = 0 0 -0.5 -0.5 - 0 = -0.5 0.25

16. Psychology vs. Biology 10 50 µ X = 60 X Psychology 4 48 µ X = 56 X Biology 52

17. Converting Distributions of Scores

18. Original vs. standardized distribution 14 57 µ Joe X = 64 z = +0.50 X Original Distribution 10 50 µ X Standardized Distribution Maria X = 43 z = -1.00 Maria X = 40 z = -1.00 Joe X = 55 z = +0.50

19. Correlating Two Distributions of Scores with z-scores

20. Distributions of height and weight  = 4 µ = 68 Person A Height = 72 inches Distribution of adult heights (in inches)  = 16 µ = 140 Person B Weight = 156 pounds Distribution of adult weights (in pounds)