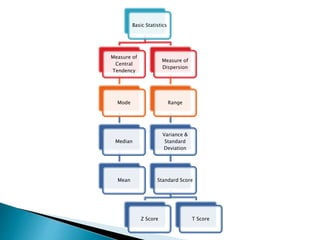
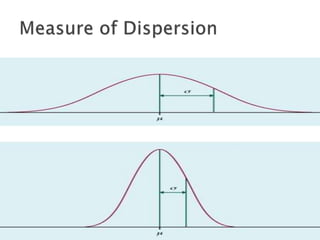
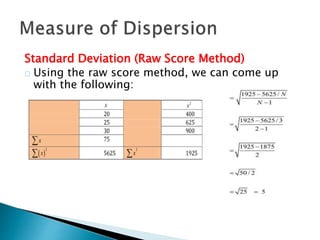
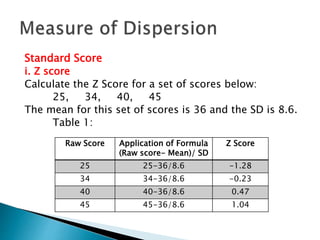
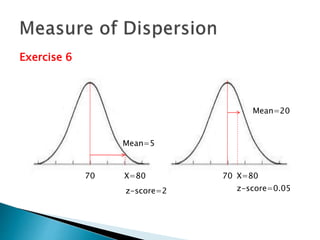
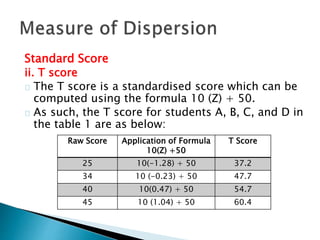
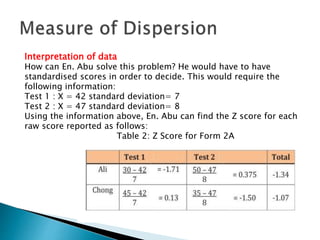
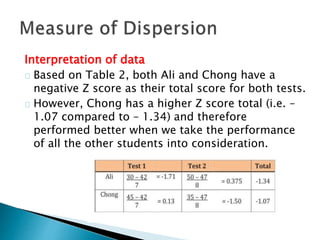
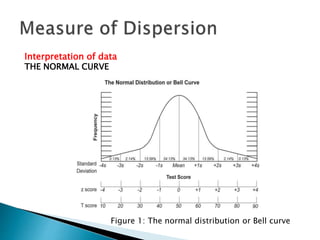
This document discusses various statistical measures used to summarize and describe data, including measures of central tendency (mean, median, mode) and measures of dispersion (range, variance, standard deviation). It provides definitions and examples of calculating each measure. Standardized scores like z-scores and t-scores are also introduced as ways to compare performance across different tests or distributions. Exercises are included for readers to practice calculating and interpreting these common descriptive statistics.

1. Lecturer: Yee Bee Choo
IPGKTHO

2. Basic Statistics
Measure of
Central
Tendency
Mode
Median
Mean
Measure of
Dispersion
Range
Variance &
Standard
Deviation
Standard Score
Z Score T Score

3. Two kinds of measures:
1. Measures of central tendency
2. Measures of dispersion
Both these types of measures are useful in
score reporting.
They are frequently used to describe data.
These are often called descriptive statistics
because they can help you describe your
data.

4. Central tendency measures the extent to
which a set of scores gathers around.
There are three major measures of central
tendency:
1. Mode
2. Median
3. Mean

5. Mode
◦ The “mode” for a set of data is the number (or item) that
occurs most frequently.
◦ Sometimes data can have more than one mode. This
happens when two or more numbers (or items) occur an
equal number of times in the data.
◦ A data set with two modes is called bimodal.
◦ A data set with 3 modes is called trimodal
◦ It is also possible to have a set of data with no mode.

6. Mode
Mode is the most common number
To find the mode, put the numbers in order,
choose the number that appears the most
frequently.
Data: 3, 5, 5, 6, 4, 3, 2, 1, 5, 6
Put in order: 1, 2, 3, 3, 4, 5, 5, 5, 6, 6
The mode is 5.

7. Mode
Bimodal
Data: 2, 5, 2, 3, 5, 4, 7
2, 2, 3, 4, 5, 5, 7
Modes = 2 and 5
Trimodal
Data: 2, 5, 2, 7, 5, 4, 7
2, 2, 4, 5, 5, 7, 7
Modes = 2, 5, and 7

8. Mode
Data: 3, 5, 6, 4, 7, 8, 9, 2, 1, 0
What is the mode?
0,1,2,3,4,5,6,7,8,9
Is the mode = 0?
Mode = no mode

9. Mode
The mode can be useful for dealing with
categorical data. For example, if a sandwich
shop sells 10 different types of sandwiches,
the mode would represent the most popular
sandwich.
The mode can be useful for summarising
survey data or election votes.

10. Median
A median is a measure of the "middle" value of
a set of data.
To find the median, put the numbers in order
and find the middle number.
If the total number of values in the sample is
even, the median is calculated by finding the
mean of the two values in the middle.
Data: 45, 47, 50, 51, 52, 54, 65
Median = 51

11. Median
Data: 45, 47, 50, 51, 52, 54, 65
Median = 51
Data: 45, 47, 50, 51, 52, 53, 54, 65
Median =(51 + 52)/2
= 51.5

12. Mean
The ‘Mean’ is the ‘Average’ value of numerical
data.
The Mean (or average) is found by adding all
scores together and dividing by the number of
scores.

13. Mean
Data: 3, 5, 5, 6, 4, 3, 2, 1, 5, 6
Add up the numbers:
3 + 5 + 5 + 6 + 4 + 3 + 2 + 1 + 5 + 6 = 40
Divide by how many numbers:
40 ÷ 10 = 4
Mean = 4

14. Exercise 1
Below is a set of marks obtained by 7
students:
82 55 73 48 88 67 67
Find the mean, mode and median.

15. Exercise 2
On a standardised reading test, the nationwide average for Year 3
pupils is 7.0. A teacher is interested in comparing class reading
scores with the national average. The scores for the 16 pupils in this
class are as follows:
8, 6, 5, 10, 5, 6, 8, 9,
7, 6, 9, 5, 14, 4, 7, 6
a) Find the mean and the median reading scores for this class.
b) If the mean is used to define the class average, how does this
class compare with the national norm?
c) If the median is used to define the class average, how does this
class compare with the national norm?

16. Measure of Dispersion tells about the spread
of scores in a data set.
There are three major measures of
dispersion:
1. Range
2. Standard deviation
3. Variance

17. Consider these means for weekly candy bar
consumption.
X = {7, 8, 6, 7, 7, 6, 8, 7}
X = (7+8+6+7+7+6+8+7)/8
X = 7
X = {12, 2, 0, 14, 10, 9, 5, 4}
X = (12+2+0+14+10+9+5+4)/8
X = 7
What is the difference?

19. How well does the mean represent the scores in a
distribution?
The logic here is to determine how much spread is
in the scores. How much do the scores "deviate"
from the mean? Think of the mean as the true
score or as your best guess. If every X were very
close to the Mean, the mean would be a very good
predictor.
If the distribution is very sharply peaked then the
mean is a good measure of central tendency and if
you were to use the mean to make predictions you
would be right or close much of the time.

20. Range
A range represents the distance on a numeric
scale from the minimum to the maximum.
You can calculate the range by subtracting
the minimum value from the maximum value.
Range = maximum - minimum
If the maximum grade was 100 and the
minimum was 55, the range would be
Range= 100-55
= 45.

21. Variance & Standard Deviation
The variance and standard deviation describe
how far or close the numbers or observations of
a data set lie from the mean (or average).
Variance is the measure of the average distance
between each of a set of data points and their
mean value; equal to the sum of the squares of
the deviation from the mean value.
Standard deviation though calculated as the
square root of the variance is the absolute value
calculated to indicate the extent of deviation
from the average of the data set.

22. Variance & Standard Deviation
Formulae:
Variance:
2 ( )i X X
s

N
  2
( X 
X
)s
2 i N
 
Standard Deviation:

23. Standard Deviation
Standard deviation refers to how much the
scores deviate from the mean.
There are two methods of calculating
standard deviation which are the deviation
method and raw score method which are
illustrated by the following formulae.

24. Standard Deviation (Deviation Method)
To illustrate this, we will use 20, 25,30. Using
standard deviation method, we come up with
the following table:

25. Standard Deviation (Raw Score Method)
Using the raw score method, we can come up
with the following:

26. Standard Deviation
Both methods result in the same final value of 5.
If you are calculating standard deviation with a
calculator, it is suggested that the deviation
method be used when there are only a few scores
and the raw score method be used when there are
many scores.
This is because when there are many scores, it will
be tedious to calculate the square of the
deviations and their sum.

27. Exercise 3
Calculate the range, variance and standard
deviation for the following sample.
41, 17, 25, 34, 14, 40, 27, 19, 50, 39
26, 22, 28, 18, 42, 33, 25, 28, 27, 33
34, 7, 12, 36, 34, 16, 49, 19, 40, 28,
26, 30, 48, 33, 33, 25, 50, 29, 26, 30

28. Standard Score
Standardised scores are necessary when we
want to make comparisons across tests and
measurements.
Z scores and T scores are the more common
forms of standardised scores.
A standardised score can be computed for
every raw score in a set of scores for a test.

29. Exercise 4
Consider the two sets of scores below:
A= 10, 36, 38, 40, 42, 44, 70
B= 10, 12, 14, 40, 66, 68, 70
Find the range and mean.

30. Standard Score
Both set A and set B have the same range and
mean.
However, set B is more dispersed. The
difference between the value 70 and other
values is more significant than set A.
To make a comparison more clearly, we can
standardised the score, by transforming it into
another distribution.

31. Standard Score
i. Z score
The Z score is the basic standardised score. It is referred to as the
basic form as other computations of standardised scores must first
calculate the Z score. The formula is as follows:

32. Standard Score
i. Z score
Calculate the Z Score for a set of scores below:
25, 34, 40, 45
The mean for this set of scores is 36 and the SD is 8.6.
Table 1:
Raw Score Application of Formula
(Raw score- Mean)/ SD
Z Score
25 25-36/8.6 -1.28
34 34-36/8.6 -0.23
40 40-36/8.6 0.47
45 45-36/8.6 1.04

33. Standard Score
i. Z score

34. Exercise 5
Ahmad obtained 90 marks (total mark is
100) in English test. The mean for the
achievement of the whole class is 70 and the
standard deviation (SD) is 25. In a
Mathematics test, Ahmad obtained 60
marks. The mean achievement for
Mathematics for the whole class is 40 while
the SD is 15. In which subject does Ahmad
score better?

35. Exercise 6
A distribution of scores has a mean of 70. In
this distribution, a score of x=80 is located
10 points above the mean.
a) Calculate z-scores for standard deviation 5
and 20.
b) Sketch the distribution and locate the
position of x=80. Compare the two z-scores
which corresponds to x=80.

36. Exercise 6
Mean=5
Mean=20
70 X=80 70 X=80
z-score=2 z-score=0.05

37. Standard Score
i. Z score
Z score values are very small and usually range only
from –2 to 2.
Such small values make it inappropriate for score
reporting especially for those unaccustomed to the
concept.
Imagine what a parent may say if his child comes
home with a report card with a Z score of 0.80 in
English Language!
Fortunately, there is another form of standardised
score - the T score – with values that are more
palatable to the relevant parties.

38. Standard Score
ii. T score
The T score is a standardised score which can be
computed using the formula 10 (Z) + 50.
As such, the T score for students A, B, C, and D in
the table 1 are as below:
Raw Score Application of Formula
10(Z) +50
T Score
25 10(-1.28) + 50 37.2
34 10 (-0.23) + 50 47.7
40 10(0.47) + 50 54.7
45 10 (1.04) + 50 60.4

39. Standard Score
ii. T score
These values seem perfectly appropriate
compared to the Z score.
The T score average or mean is always 50 (i.e.
a standard deviation of 0) which connotes an
average ability and the mid point of a 100
point scale.

40. Interpretation of data
The standardised score is actually a very important
score if we want to compare performance across tests
and between students. Let us take the following
scenario as an example:

41. Interpretation of data
How can En. Abu solve this problem? He would have to have
standardised scores in order to decide. This would require the
following information:
Test 1 : X = 42 standard deviation= 7
Test 2 : X = 47 standard deviation= 8
Using the information above, En. Abu can find the Z score for each
raw score reported as follows:
Table 2: Z Score for Form 2A

42. Interpretation of data
Based on Table 2, both Ali and Chong have a
negative Z score as their total score for both tests.
However, Chong has a higher Z score total (i.e. –
1.07 compared to – 1.34) and therefore
performed better when we take the performance
of all the other students into consideration.

43. Interpretation of data
THE NORMAL CURVE
The normal curve is a hypothetical curve that is
supposed to represent all naturally occurring
phenomena.
Test scores that measure any characteristic such
as intelligence, language proficiency or writing
ability of a specific population is also expected to
provide us with a normal curve.
The following is a diagram illustrating how the
normal curve would look like.

44. Interpretation of data
THE NORMAL CURVE
Figure 1: The normal distribution or Bell curve

45. Interpretation of data
THE NORMAL CURVE
The normal curve in Figure 1 is partitioned according
to standard deviations (i.e. – 4s, -3s, + 3s, + 4s)
which are indicated on the horizontal axis.
The area of the curve between standard deviations is
indicated in percentage on the diagram.
For example, the area between the mean (0 standard
deviation) and +1 standard deviation is 34.13%.
Similarly, the area between the mean and –1 standard
deviation is also 34.13%. As such, the area between –1
and 1 standard deviations is 68.26%.

46. Interpretation of data
THE NORMAL CURVE
In using the normal curve, it is important to
make a distinction between standard deviation
values and standard deviation scores.
A standard deviation value is a constant and is
shown on the horizontal axis of the diagram
above.

47. Interpretation of data
THE NORMAL CURVE
The standard deviation score, on the other hand,
is the obtained score when we use the standard
deviation formula provided earlier.
So, if we find the score to be 5 as in the earlier
example, then the score for the standard
deviation value of 1 is 5 and for the value of 2 is 5
x 2 = 10 and for the value of 3 is 15 and so on.
Standard deviation values of –1, -2, and –3 will
have corresponding negative scores of –5, -10,
and –15.