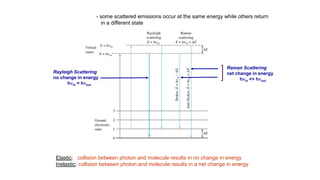
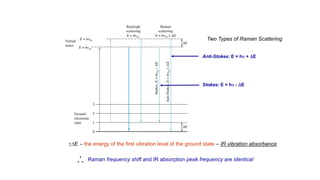
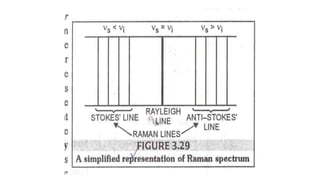
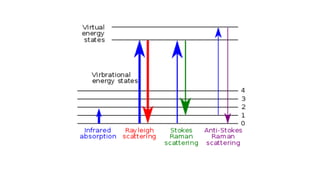
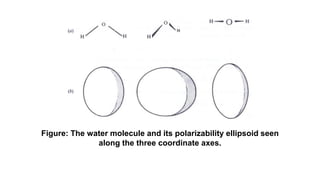
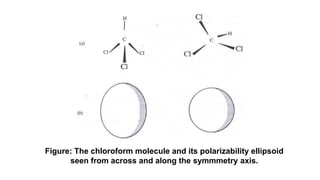
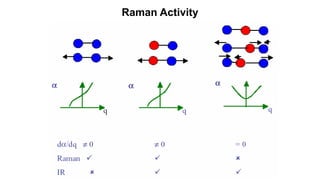
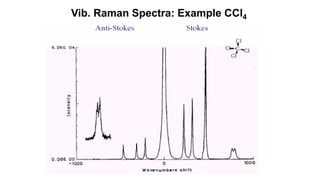
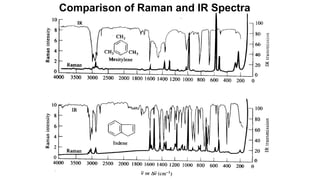
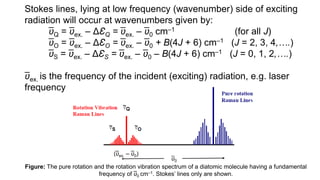
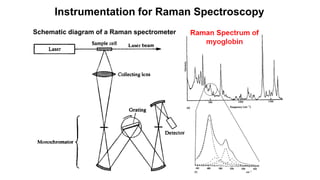
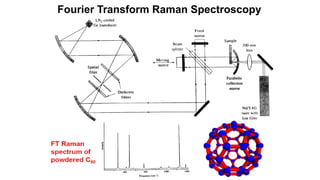
The document discusses Raman spectroscopy, which analyzes the scattering of light by molecules rather than light absorption. When a sample is irradiated with monochromatic light, most light is Rayleigh scattered at the same frequency, but a small amount is Raman scattered at lower (Stokes) or higher (anti-Stokes) frequencies. The frequency shift between incident and scattered light is independent of the incident light frequency and depends on molecular structure. Raman scattering occurs due to changes in molecular polarizability during vibrations or rotations. Spectra provide information about molecular vibrational and rotational energy levels.

1. Raman spectra
This is based on scattering of radiation and not
on the absorption of radiation by the sample.

2. RAMAN SPECTRA
GENERAL INTRODUCTION
It is a type of spectroscopy which deals not with the
absorption of electromagnetic radiation but deals with the
scattering of light by the molecules. When a substance
which may be gaseous, liquid or even solid is irradiated with
monochromatic light of a definite frequency v, a small
fraction of the light is scattered. Rayleigh found that if the
scattered light is observed at right angles to the direction of
the incident light, the scattered light is found to have the
same frequency as that of the incident light. This type of
scattering is called Rayleigh scattering.

3. energy absorbed by molecule
from photon of light
not quantized
No change in
electronic states
Infinite number
of virtual states

4. When a substance is irradiated with monochromatic light of a
definite frequency v, the light scattered at right angles to the
incident light contained lines not only of the incident frequency
but also of lower frequency and sometimes of higher
frequency as well. The lines with lower frequency are called
Stokes' lines whereas lines with higher frequency are called
anti-Stokes' lines.
Raman further observed that the difference between the
frequency of the incident light and that of a particular scattered
line was constant depending only upon the nature of the
substance being irradiated and was completely independent of
the frequency of the incident light. If vi is the frequency of the
incident light and vs that of particular scattered line, the
difference v = vi - vs is called Raman frequency or Raman
shift.

5. - some scattered emissions occur at the same energy while others return
in a different state
Rayleigh Scattering
no change in energy
hnin = hnout
Elastic: collision between photon and molecule results in no change in energy
Inelastic: collision between photon and molecule results in a net change in energy
Raman Scattering
net change in energy
hnin <> hnout

6. Anti-Stokes: E = hn + DE
Two Types of Raman Scattering
Stokes: E = hn - DE
DE – the energy of the first vibration level of the ground state – IR vibration absorbance
Raman frequency shift and IR absorption peak frequency are identical


8. EXPLANATION FOR OBSERVING RAYLEIGH
LINE AND RAMAN LINES
• Elastic and inelastic collisions between the
radiations and interacting molecules results in
the formation of Rayleigh and Raman lines.
• In terms of excitation of electrons
• vabs = ve Rayleigh line
• vabs > ve Stokes line
• vabs < ve Anti Stokes line

10. POLARIZABILITY OF MOLECULES
AND RAMAN SPECTRA
• The Raman effect arises on account of the
polarization (distortion of the electron cloud) of the
scattering molecules that is caused by the electric
vector of the electromagnetic radiation. The induced
dipole moment (μ) depends upon the magnitude of the
applied field, E, and the ease with which the molecule
can be distorted. We may write
μ= αE
where α is the polarizability of the molecule.

11. Consider first the diatomic molecule H2 placed in an electric
field, which shows end-on and sideways orientation,
respectively. The electrons forming the bond are more easily
displaced by the field along the bond axis (Figure: b) than
that across the bond (Figure: a) and the polarizability is thus
said to be anisotropic. The polarizability of a molecule in
various directions is conventionally represented by drawing
a polarizability ellipsoid (Figure c & d).
Figure: The hydrogen molecule in an electric field and its polarizability
ellipsoid seen along and across the bond axis.

12. All diatomic molecules have ellipsoids of the same
general tangerine shape as H2, as do linear polyatomic
molecules, such as CO2, H2C2, etc. They differ only in the
relative sizes of their major and minor axes.
When a sample of such molecules is subjected to a beam
of radiation of frequency ʋ the electric field experienced
by each molecule varies according to the equation
E = E0 sin 2πʋt (1)
and thus the induced dipole also undergoes oscillations of
frequency ʋ:
μ = αE = αE0 sin 2πʋt (2)
Eq.(3) is the classical explanation of Rayleigh scattering.

13. If the molecule undergoes some internal motion, such as
vibration or rotation, which changes the polarizability
periodically, then the oscillating dipole will have
superimposed upon it the vibrational or rotational
oscillation. Consider a vibration of frequency ʋvib which
changes the polarizabilty: we can write
α = α0 + βsin 2πʋvibt (3)
where α0 is the equilibrium polarizability and β represents
the rate of change of polarizability with the vibration. Then
we have:
μ = αE = (α0 + βsin 2πʋvibt)E0 sin 2πʋt
or, expanding and using the trigonometric relation:
sin A sin B = ½ {cos(A – B) – cos(A + B)}

14. We have
μ = α0E0 sin 2πʋt + ½ βE0{cos 2π(ʋ – ʋvib)t – cos 2π(ʋ + ʋvib)t} (4)
and thus the oscillating dipole has frequency components (ʋ ± ʋvib) as
well as the exciting frequency (ʋ).
The general rule: In order to be Raman active a molecular rotation or
vibration must cause some change in a component of the molecular
polarizability. A change in polarizability is reflected by a change in either
the magnitude or the direction of the polarizability ellipsoid.

15. Figure: The water molecule and its polarizability ellipsoid seen
along the three coordinate axes.

16. Figure: The chloroform molecule and its polarizability ellipsoid
seen from across and along the symmmetry axis.

17. Types of molecules showing Rotational Raman Spectra
• A molecule scatters light because it is polarizable. Hence the
gross selection rule for a molecule to give a rotational Raman
spectrum is that the polarizability of the molecule must be
anisotropic i.e. the polarizability of the molecule must depend upon
the orientation of the molecule with respect to the direction of the
electric field.
• Hence all diatomic molecules, linear molecules and non-spherical
molecules give Raman spectra i.e. they are rotationally Raman
active. On the other hand, spherically symmetric molecules such
as CH4, SF6 etc. do not give rotational Raman spectrum i.e. they
are rotationally Raman inactive. (These molecules are also
rotationally microwave inactive).

18. PURE ROTATIONAL RAMAN SPECTRA
Linear Molecules
The rotational energy levels of linear molecules have already been
stated by the equation
ƐJ = BJ(J+1) – DJ2(J+1)2 cm–1 (J = 0, 1, 2,…..)
In Raman spectroscopy the precision of the measurements does not
normally warrant the term involving the centrifugal distortion constant,
D. Thus we take the simpler expression:
ƐJ = BJ(J+1) cm–1 (J = 0, 1, 2,…..)
to represent the energy levels.

19. Transitions between these levels follow the formal selection rule:
ΔJ = 0, or ±2 only
The selection rule ΔJ = 0 corresponds to Rayleigh scattering
where as selection rule ΔJ = ±2 gives rise to Raman lines as
explained.
As explained earlier, the intensities of lines depend upon the
population of initial level from where the molecules are excited or
de-excited to the final level. Since the population of rotational
energy levels is as shown in Fig. therefore the intensities of the
Stokes' and anti-Stokes' lines vary in a similar manner.

21. Symmetric top molecule
Only end-over-end rotations produce a change in the polarizability
in the case of the symmetric top molecules (a molecule in which
two moments of inertia are the same).
The energy levels:
ƐJ, K = BJ(J+1) + (A–B)K2 cm–1
(J = 0, 1, 2,…..; K = ±J, ±(J–1), ….)
The Raman selection rules for a symmetric top molecule are:
ΔK = 0
ΔJ = 0, ±1, ±2 (except for K=0 states, when ΔJ = ±2 only)

22. (1) ΔJ = ±1 (R branch)
Lines at ΔER = 2B(J+1) J = 1, 2, .. but J ≠ 0
(2) ΔJ = ±2 (S branch)
Lines at ΔES = 2B(2J+3) J = 0, 1, 2, ..
The spectrum shows a complex intensity
structure (not to be confused with nuclear
spin effects), but the basic line spacing is
now 2B, rather than 4B as in the case of
linear molecules.
A symmetric top molecule has anisotropic polarizability. This selection rule
holds for any K. There are two cases:
The rotational Raman spectrum
of a symmetric top molecule

23. VIBRATIONAL RAMAN SPECTRA
Raman Activity of Vibration
The change in size, shape or
direction of the polarizability
ellipsoid of the water molecule
during each of the three
vibrational modes. The center
column shows the equilibrium
position of the molecule, while to
right and left are the extremes of
each vibration.

24. The changes in polarizability
ellipsoid of carbon dioxide
during its vibrations, and a
graph showing the variation
of the polarizability, α, with
the displacement coordinate,
ξ, during each vibration.

25. Raman Activity

26. 1- Atomic number Z:
P  the amount of electrons,
Electrons become less control by nuclear charge.
2- Bond Length:
P  Bond Length
3- Atomic or Molecular Size:
P  Size,
4- Molecular orientation with respect to an electric field
Parallel or perpendicular (Exp: Parallel has more effect)
5- Bond Strength (Bond order):
P  1/strength of bond C=C, and C≡C, C≡N bonds are
strong scatterers, bonds undergo polarization.
6- Electronegativity difference:
P  1/ difference in electronegativity
7- Covalent bonds more polarizable than ionic bonds.
Factors affect Polarizability

27. Structure of Vibrational Raman Spectra
For every vibrational mode of the molecule, the energy of the
mode is given by
Ɛ = ϖe(ʋ +
1
2
) – ϖexe(ʋ+
1
2
)2 cm–1 (ʋ = 0, 1, 2,…..) (1)
where, ϖe is the equilibrium vibrational frequency expressed in
wavenumbers and xe is the anharmonicity constant. The
selection rule:
Δʋ = 0, ±1, ±2, …. (2)
which is the same for Raman as for infra-red spectroscopy, the
probability of Δʋ = ±2, ±3, …. decreasing rapidly.

28. For Raman active modes, we can apply the selection rule (eq. 2)
to the energy level expression (eq. 1) and obtain the transition
energies:
ʋ = 0 → ʋ = 1: Δɛfundamental = ϖe(1 – 2xe) cm–1
ʋ = 0 → ʋ = 2: Δɛovertone = 2ϖe(1 – 3xe) cm–1
ʋ = 1 → ʋ = 2: Δɛhot = ϖe(1 – 4xe) cm–1
However, since the Raman Scattering Process is very weak, we
can ignore all processes such as Overtones and Hot bands
since these are weak even in IR spectra. So we only need to
consider the fundamental transitions ʋ = 0 → ʋ =1. In other
words we can write
ʋfundamental = ʋex. ± Δɛfundamental cm–1
where the minus sign represents the Stokes’ lines and the plus
sign refers to the anti-Stokes’ lines.

29. Example: CHCl3 molecule.
Symmetric top molecule with 5 atoms ⇒ 3N - 6
= 15 - 6 = 9 vibrational modes, however, due to
symmetry 3 modes are degenerate ⇒ 6
vibrational modes.
Modes are seen at 262, 366, 668, 761, 1216
and 3019 cm-1. All six modes are both IR and
Raman active. Exciting source is Ar 488 nm
laser line.
In the Raman spectrum on the left the
wavenumber of the incident (laser) radiation is
set to zero, so x-axis shows wavenumbers of
the vibrational modes (and not absolute values).
Vibrational Raman Spectra

30. In general for polyatomic molecules it is usually necessary to apply Group
Theory in order to decide whether a particular vibration of the molecule is
Raman active or not. But some general rules apply:
If the molecule has no symmetry (e.g. HCN) then usually all of its
vibrational modes are Raman active.
In molecules that possess symmetry (e.g. CO2, H2O) then
Symmetric vibrations give rise to intense Raman lines, non symmetric
vibrations are usually weak and sometimes unobservable. In particular
bending modes usually yield a very weak Raman line.
Raman Activity in Polyatomic Molecules

31. Rule of Mutual Exclusion:
If the molecule has a centre of symmetry, then
Raman active vibrations are infrared inactive and
vice versa. If there is no centre of symmetry in the
molecule then some or all of the vibrations may be
both Raman and IR active.

32. Vib. Raman Spectra: Example CCl4

33. Comparison of Raman and IR Spectra

34. Vibrational-Rotational Raman spectroscopy
The fine structure is rarely resolved except in the case of diatomic
molecules. We can write the vib-rot energy levels as:
ƐJ,ʋ = ϖe(ʋ+
1
2
) – ϖexe(ʋ+
1
2
)2 + BJ(J+1) cm–1
(ʋ = 0, 1, 2,…..; J = 0, 1, 2,……)
where we have ignored the centrifugal distortion (D term).
For diatomic molecules ΔJ = 0, ± 2 and combining this with the
fundamental transition ʋ = 0 → ʋ = 1 gives
Q-Branch ΔJ = 0: ΔƐQ = ʋ0 cm–1 (for all J)
S-Branch ΔJ = +2: ΔƐS = ʋ0 + B(4J + 6) cm–1 (J = 0, 1, 2,….)
O-Branch ΔJ = –2: ΔƐO = ʋ0 – B(4J + 6) cm–1 (J = 2, 3, 4,….)

35. Stokes lines, lying at low frequency (wavenumber) side of exciting
radiation will occur at wavenumbers given by:
ʋQ = ʋex. – ΔƐQ = ʋex. – ʋ0 cm–1 (for all J)
ʋO = ʋex. – ΔƐO = ʋex. – ʋ0 + B(4J + 6) cm–1 (J = 2, 3, 4,….)
ʋS = ʋex. – ΔƐS = ʋex. – ʋ0 – B(4J + 6) cm–1 (J = 0, 1, 2,….)
ʋex. is the frequency of the incident (exciting) radiation, e.g. laser
frequency
(ʋex. – ʋ0)
ʋ0
Figure: The pure rotation and the rotation vibration spectrum of a diatomic molecule having a fundamental
frequency of ʋ0 cm–1. Stokes’ lines only are shown.

36. Instrumentation for Raman Spectroscopy
Schematic diagram of a Raman spectrometer

37. Fourier Transform Raman Spectroscopy