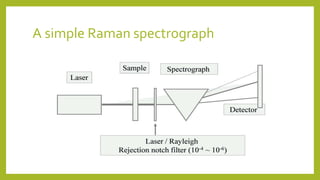
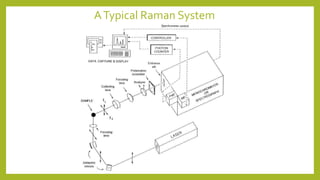
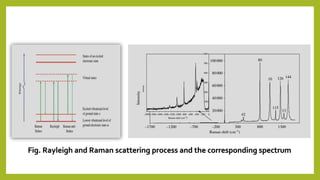
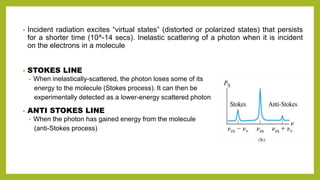
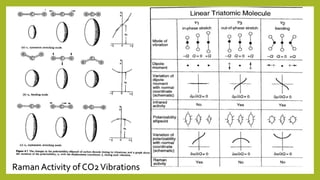
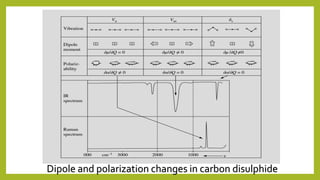
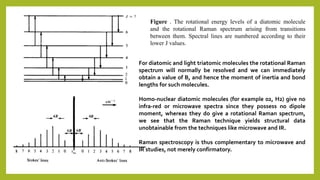
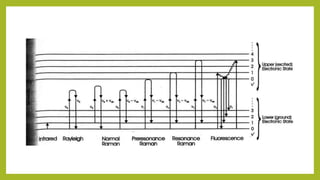
Raman spectroscopy is a spectroscopic technique used to observe vibrational, rotational, and other low-frequency modes in a system. It relies on inelastic scattering, or Raman scattering, of monochromatic light, usually from a laser in the visible, near infrared, or near ultraviolet range. The laser light interacts with molecular vibrations, phonons or other excitations in the system, resulting in the energy of the laser photons being shifted up or down. The shift in energy gives information about the vibrational modes in the system. Raman spectroscopy is commonly used in chemistry to provide a fingerprint by which molecules can be identified. It can also be used to elucidate details of molecular structure.

1. RAMAN SPECTROSCOPY
Pema Chida Sherpa
21PDPY01

2. CONTENTS
• INTRODUCTION
• RAYLEIGH SCATTERING
• STOKESANDANTI-STOKES Line
• QUANTUMTHEORY
• MOLECULAR POLARISABILITY
• RAMANACTIVITYOF H2OAND OTHER MOLECULE
• Rule of Mutual Exclusion
• PURE ROTATIONAL RAMAN SPECTRA
• TYPES OF RAMAN SPECTRA
• ADVANTAGES OF RAMAN SPECTROSCOPYOVER IR SPECTROSCOPY
• ADVANTAGES OF IR SPECTROSCOPYOVER RAMAN SPECTROSCOPY

4. • It is widely used to provide information on chemical structures and physical
forms of atoms and molecules.
• It is used to identify substances from the characteristic spectral patterns
(‘fingerprinting’) and
• to determine quantitatively or semi quantitatively the amount of a substance in a
sample.
• Studying the spectral emission lines of the sun and distant galaxies.
• Space exploration.

5. Light Scattering Phenomenon
• When radiation passes through a transparent medium,
the species present in that medium scatter a fraction of
the beam.
• Scattering can be elastic or inelastic in nature.
• Phenomenon of inelastic scattering of light was first
postulated by A. Smekal In 1923 and first observed
experimentally in 1928 by C.V. Raman and K.S.
Krishnan.
• Scattering is widely used as a method for measuring
particle size and size distribution down to sizes less than 1
μm.

7. What is Raman Spectroscopy(or Raman
Effect)?
• In 1928, the Indian physicist C. V. Raman discovered that the visible wavelength
of a small fraction of the radiation scattered by certain molecules differs from
that of the incident beam.
• He noticed that the change (shifts) in frequency depend upon the chemical
structure of the molecules responsible for the scattering.
• In original experiment, sunlight was focused by a telescope onto a sample,
which was either a purified liquid or a dust‐free vapor. A second lens was placed by
the sample to collect the scattered radiation. A system of optical filters was used
to show the existence of scattered radiation with an altered frequency from the
incident light –the basic characteristic of Raman scattering.

8. First photographed Raman spectra.

9. A simple Raman spectrograph

10. ATypical Raman System

11. Rayleigh and Raman
• Rayleigh scattering:
• occurs when incident EM radiation induces an oscillating dipole in a
molecule, which is re-radiated at the same frequency.
• Raman scattering:
• occurs when monochromatic light is scattered by a molecule, and the scattered
light has been weakly modulated by the characteristic frequencies of the
molecule.
• STOKES LINE
• ANTI-STOKES LINE

12. Fig. Rayleigh and Raman scattering process and the corresponding spectrum

13. • Incident radiation excites “virtual states” (distorted or polarized states) that persists
for a shorter time (10^-14 secs). Inelastic scattering of a photon when it is incident
on the electrons in a molecule
• STOKES LINE
• When inelastically-scattered, the photon loses some of its
energy to the molecule (Stokes process). It can then be
experimentally detected as a lower-energy scattered photon
• ANTI STOKES LINE
• When the photon has gained energy from the molecule
(anti-Stokes process)

14. QuantumTheory
• It treats radiation of frequency v as consisting of a stream of particles (called
photons) having energy hv where h is Planck's constant.
• Photons can be imagined to undergo collisions with molecules and, if the collision is
perfectly elastic, they will be deflected unchanged. It can be likened to a ball bearing
striking a rigid table-the ball bearing bounces off the table without any loss of
energy.
• There can be exchange of energy between photon and molecule(inelastic collision).
The molecule can gain or lose amounts of energy only in accordance with the
quantal laws; i.e. its energy change, ΔE joules, must be the difference in energy
between two of its allowed states.
• Δ E must represent a change in the vibrational and/or rotational energy of the
molecule. If the molecule gains energy Δ E, the photon will be scattered with energy
hv - Δ E and the equivalent radiation will have a frequency v - Δ E/h. Conversely, if
the molecule loses energy AE, the scattered frequency will be v + Δ E/h.

15. • A change in the molecular polarization potential – or the amount of deformation of the
electron cloud – with respect to the vibrational coordinate is required for the molecule to
exhibit a Raman effect.
• Polarizability is the relative tendency of a charge distribution, like the electron cloud of an
atom or molecule, to be distorted from its normal shape by an external electric field, which
may be caused by the presence of a nearby ion or dipole or by an applied external electric
field.
• The amount of the polarizability change will determine the Raman scattering intensity.
• This dependence on the molecular polarizability differs from the IR spectroscopy where
the interaction between the molecule and the light is determined by the dipole moment ;
this contrasting feature allows to analyze transitions that might not be IR active via Raman
spectroscopy, as illustrated by the rule of mutual exclusion in centrosymmetric molecules.
Molecular Polarizability

16. • Amount of polarization μ in most materials Is proportional to the magnitude
of the applied electric field and on the ease with which the molecule can be
distorted.
𝜇 = 𝛼𝐸
Where 𝛼 is the polarizability of the molecule.
• polarizability of a molecule in various directions is conventionally
represented by drawing a polarizability ellipsoid.

17. Raman Activity of MolecularVibrations
• In order to be Raman active, a molecular rotation or vibration must cause
some change in a component of the molecular polarizability. The change
can either be in the magnitude or the direction of the polarizability ellipsoid.
• Polarizability ellipsoid is a three-dimensional body generated by plotting
1/√α from the center of gravity in all directions.
• where the polarizability is greatest, the axis of the ellipsoid is least, and vice
versa.
• This rule must be contrasted with that for IR activity that requires change in
the net dipole moment of the molecule.

18. Raman
Activity of
H2O
Vibrations

19. Raman Activity of CO2Vibrations

20. Dipole and polarization changes in carbon disulphide

21. Inference
• From above figures we can see that Raman spectrum is forbidden for
dα/dξ = 0 but allowed for dα/dξ ≠ 0 we can imagine that the 'degree of
allowedness‘ varies with dα/dξ .
• . Thus if the polarizability curve has a large slope at J = 0 the Raman line
will be strong; if the slope is small it will be weak; and if zero, not allowed at
all.
• Symmetric vibrations give rise to intense Raman lines; non-symmetric ones
are usually weak and sometimes unobservable.
• a bending motion usually yields only a very weak Raman line

22. Rule of Mutual Exclusion
• If a molecule has a centre of symmetry, then Raman active vibrations are
infrared inactive, and vice versa. If there is no center of symmetry, then
some (but not necessarily all) may be both Raman and infrared active.
• The converse of this rule is also true, i.e. the observance of Raman and
infra-red spectra showing no common lines implies that the molecule has a
centre of symmetry
*caution is necessary since a vibration may be raman active but too weak to be observed .

23. Number of bands in Raman spectrum
• A linear molecule of N atoms has (3 translational deg. Freedom + 2
rotational ) = 3N-5 normal modes of vibration
• Non-linear molecule: 3N-6 modes
• As for an IR spectrum, the number of bands in the Raman spectrum for an
N-atom non-linear molecule is seldom 3N-6, because:
• polarizability change is zero or small for some vibrations;
• bands overlap;
• combination or overtone bands are present;
• Fermi resonances occur;
• some vibrations are highly degenerate; etc…

24. PURE ROTATIONAL RAMAN SPECTRA
• 1. Linear Molecules:
𝜀𝐽 = 𝐵𝐽(𝐽 + 1) where ΔJ=0, or ±2 only.
ΔJ=0 is a trivial Rayleigh scattering only.
ΔJ=-2 cannot exist for a pure rotational change so
For ΔJ=+2 we have
Δε = 𝜀𝐽′=𝐽+2 − 𝜀𝐽′′=𝐽
=B(4J+6) 𝑐𝑚−1 S branch lines (for ΔJ=+2 )
The wavenumbers of the corresponding spectral lines are given by
𝑣𝑠 = 𝑣𝑒𝑥 ± ∆𝜀𝑠 = 𝑣𝑒𝑥 ± B(4J+6) 𝑐𝑚−1
Where positive sign refers to anti- Stoke’s lines and the minus sign to Stoke’s lines
and 𝑣𝑒𝑥 is the wavenumber of the exciting radiation.

25. Figure . The rotational energy levels of a diatomic molecule
and the rotational Raman spectrum arising from transitions
between them. Spectral lines are numbered according to their
lower J values.
For diatomic and light triatomic molecules the rotational Raman
spectrum will normally be resolved and we can immediately
obtain a value of B, and hence the moment of inertia and bond
lengths for such molecules.
Homo-nuclear diatomic molecules (for example 02, H2) give no
infra-red or microwave spectra since they possess no dipole
moment, whereas they do give a rotational Raman spectrum,
we see that the Raman technique yields structural data
unobtainable from the techniques like microwave and IR.
Raman spectroscopy is thus complementary to microwave and
IR studies, not merely confirmatory.

26. TYPES OF RAMAN SPECTRA
• Several variations of Raman spectroscopy have been developed. The usual purpose is to
enhance the sensitivity (e.g., surface-enhanced Raman), to improve the spatial resolution
(Raman microscopy), or to acquire very specific information (resonance Raman).
• Surface Enhanced Raman Spectroscopy (SERS)
• Resonance Raman.
• Surface-Enhanced Resonance Raman Spectroscopy (SERRS)
• Angle Resolved Raman Spectroscopy
• Hyper Raman
• Spontaneous Raman Spectroscopy (SRS)
• Optical Tweezers Raman Spectroscopy (OTRS)
• Stimulated Raman Spectroscopy
• Spatially Offset Raman Spectroscopy(SORS)

27. APPLICATIONS
• Qualitative tool for identifying molecules from their vibrations, especially in
conjunction with infrared spectrometry.
• Quantitative Raman measurements
• a) not sensitive since Raman scattering is weak. But resonance Raman spectra
offer higher sensitivity, e.g. fabric dyes studied at 30-50 ppb.
• b) beset by difficulties in measuring relative intensities of bands from different
samples, due to sample alignment, collection efficiency, laser power.
• Overcome by using internal standard.

28. FIELD OF APPLICATIONS
• Semi-conductors
• Stress, contamination, super lattices structure and defect investigations, hetero structures, doping
effects.
• Polymers
• Polymorphs identification, blend morphology, monomers and isomers analysis, crystallinity, orientation,
polymerization .
• Geology / Mineralogy/ Gemology
• Fluid inclusions, gemstones, phase transitions, mineral behavior under extreme conditions, mineral
structures
• Carbon compounds
• DLC (Diamond Like Carbon), nanotubes, Fullerenes characterization, diamond, graphite, intercalation
compounds, film quality analysis, hard-disk coatings analysis
• Life Science
• Bio-compatibility, DNA analysis, drug/cell interaction, immune globulins, nucleic acids, chromosomes,
oligosaccharides, cholesterol, lipids, cancer, metabolic accretions, inclusion of foreign materials and
pathology.

29. Advantages of Raman over IR:
• It can be used with solids and liquids
• Not interfered by water so water can be used a solvent.
• Very suitable for biological samples in native state.
• Although Raman spectra result from molecular vibrations at IR frequencies,
spectrum is obtained using visible or near IR radiation. Raman scattering does not
require matching of the incident radiation to the energy difference between the
ground and excited states
• Raman spectra are acquired quickly within seconds
• Samples can be analyzed through glass or a polymer packaging
• Laser light and Raman scattered light can be transmitted by optical fibers over long
distances for remote analysis

30. Limitations
• It is inherently a weak process in that only one in every 106–108 photons
which scatter is Raman scattered. Modern lasers and microscopes very
high‐power densities can be delivered to very small samples but it does
follow that other possible processes such as sample degradation and
fluorescence can occur readily.
• Fluorescence can often contaminate Raman spectra. The use of a Near-IR
785 nm laser radically reduces the possibility of fluorescent contamination,
but there can still be some fluorescent problems.
• More expensive
• It is not suitable for metal alloys.

31. Advantages of IR over Raman
• Simpler and cheaper instrumentation.
Less instrument dependent than Raman spectra because IR spectra
are based on measurement of intensity ratio.
• Lower detection limit than (normal) Raman.
• Background fluorescence can overwhelm Raman.
• More suitable for vibrations of bonds with very low polarizability (e.g. C–F).

33. THANKYOU